Russian Federation
Russian Federation
Russian Federation
Russian Federation
The issues of optimal control of an asynchronous motor according to the criterion of the maximum of its electromagnetic torque are considered. It is shown that electric energy converters feeding the windings of electric machines have semiconductor switches in their composition, the characteristics of which are subject to known limitations. One of these characteristics for a semiconductor key is the value of the maximum current that it can pass through itself for a long time without breaking down. The electromagnetic torque of an asynchronous electric motor with vector control is proportional to two orthogonal currents with respect to each other - magnetization and load. The magnetization current determines the magnetization of the magnetic circuit, it has a significant effect on the operating modes of the machine. The geometric sum of these currents, called the stator current modulus, forms a current that flows through the converter switches. Each of these currents has its own control circuit. The control system limits the modulus of the stator current vector at a given level. There presented the formulas for finding optimal tasks for the circuits of the above-mentioned ones, which allow to obtain the maximum electromagnetic moment under given restrictions on the modulus of the vector of the stator from the side of the electric energy converter. It is established that in order to obtain the maximum electromagnetic torque of an asynchronous motor, it is necessary to take into account the nonlinearity of its magnetization. The paper calculates the maximum electromagnetic torque for various functions approximating the magnetization curve of the magnetic circuit of an asynchronous motor, and also performs an approximate calculation of power losses. It is proved that maximizing the electromagnetic torque makes it possible to significantly expand the mechanical characteristics of the motor and electric drive.
stator current, stator current modulus, electromagnetic torque, maximization, limitations, asynchronous motor
Введение
Преобразователь частоты является неотъемлемым элементом современного электропривода переменного тока. На его основе реализуются разнообразные алгоритмы управления приводом, в том числе векторные. Топология преобразователей частоты, используемых на практике, достаточно обширна [1]. Существуют две основные группы таких преобразователей: со звеном постоянного тока (классические и каскадные схемы) [2] и непосредственные (матричные) [3]. Каждая из этих групп может быть разделена на отдельные подгруппы. Так, например, преобразователи частоты со звеном постоянного тока можно различать по количеству уровней напряжения [4], а непосредственные, или, как их еще называют, матричные, преобразователи частоты можно различать по количеству ключей в ячейке матрицы. Вместе с тем, независимо от топологии, все без исключения преобразователи частоты имеют в своем составе электронные полупроводниковые ключи. К основным параметрам таких ключей относят максимальное допустимое значение протекающего по нему тока, максимальное допустимое значение напряжения, которое может быть приложено к ключу, и т. д. Несмотря на современные уровни развития научной базы полупроводников приборов и применяемых для их создания технологий, значения вышеперечисленных параметров имеют пределы. Эти пределы определяют ограничения на электропривод и его характеристики. Одной из таких характеристик электропривода является максимальный электромагнитный момент, который может развить двигатель. Целью работы является рассмотрение вопросов управления асинхронным двигателем, при котором достигается его максимальный электромагнитный момент с учетом ограничения, накладываемого на модуль тока статора.
Максимизация момента асинхронного двигателя позволяет расширить механическую характеристику привода, предоставляя возможность эксплуатировать его в специальных режимах, когда требуется режим форсировки момента.
Методы и материалы исследования
Современные алгоритмы управления асинхронным двигателем наделяют электропривод быстродействием, высоким качеством переходных процессов и позволяют значительно повысить его энергоэффективность. Принцип действия таких алгоритмов управления основывается на представлении управляемых и контролируемых переменных в виде векторов; соответственно, называются такие алгоритмы векторным управлением [5, 6]. При векторном управлении ток статора асинхронного двигателя разделяется на две составляющие – продольную и поперечную [7]. Каждая составляющая имеет свой контур управления. Продольная составляющая называется током намагничивания и имеет обозначение id, поперечная составляющая называется током нагрузки и имеет обозначение iq. Ток статора, токи намагничивания и нагрузки связаны формулой
![]()
где ia – модуль вектора тока статора.
Фактически ток ia – это ток, протекающий по статорным обмоткам и, следовательно, по ключам преобразователя. Как отмечалось выше, максимальное значение этого тока iamax ограничено.
Электромагнитный момент асинхронного двигателя напрямую связан с токами id и iq следующим выражением:
M = Ldqidiq = ψdq(id)iq,
где Ldq = Ld – Lq – моментообразующая индуктивность; Ld – продольная индуктивность; Lq – поперечная индуктивность; ψdq(id) – продольное потокосцепление машины.
Управление электромагнитным моментом без учета нелинейности кривой намагничивания магнитопровода асинхронного двигателя
Для упрощения поставленной задачи допустим, что потокосцепление имеет линейную зависимость от тока намагничивания, а индуктивность Ldq – постоянная величина. Тогда формула электромагнитного момента примет вид:
M = Ldqidiq.
Оптимальный ток намагничивания idО, при котором достигается максимальное значение электромагнитного момента при заданных ограничениях i0 на модуль тока статора ia, определяется решением уравнения
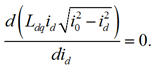
Максимальный электромагнитный момент при управлении без учета нелинейности кривой намагничивания магнитопровода будет определяться формулой
![]()
При управлении без учета нелинейности магнитопровода асинхронного двигателя значения токов, которые обеспечат максимальный электромагнитный момент, вычисляются аналитически. Аналитическое решение выглядит следующим образом:
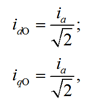
где idО и iqО – токи намагничивания и нагрузки, оптимальные по критерию максимума электромагнитного момента.
Стоит отметить, что данный алгоритм является несовершенным, т. к. при нем не учитывается нелинейность намагничивания магнитопровода. Это приводит к значительному перенасыщению машины, что влечет за собой перегрев и характеризуется достаточно большой погрешностью.
Управление электромагнитным моментом асинхронного двигателя при поддержании постоянства номинального тока намагничивания
Векторный алгоритм управления электромагнитным моментом асинхронного двигателя, при котором поддерживается номинальный ток намагничивания, является одним из самых распространенных. Его реализация значительно проще, чем у других алгоритмов векторного управления. Данный алгоритм обладает высоким быстродействием за счет того, что намагниченность машины не нужно регулировать в широком диапазоне, необходимо только поддерживать ее на номинальном уровне.
При таком управлении электромагнитный момент определяется по формуле
M = (Ldном – Lqном)idномiq.
В данной статье также произведен расчет максимального момента при таком управлении с учетом ограничения на модуль вектора статора. Данное управление может рассматриваться как базовое.
Управление электромагнитным моментом c учетом нелинейности кривой намагничивания магнитопровода асинхронного двигателя
Электромагнитный момент с учетом кривой намагничивания [8] магнитопровода асинхронного двигателя определяется формулой
M = ψdq(id)iq.
Оптимальный ток намагничивания idО при заданных ограничениях на модуль тока статора, при котором достигается максимальное значение электромагнитного момента, определяется решением уравнения
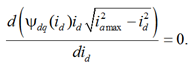
Полученное в результате решения этого уравнения значение тока id = idО и будет являться оптимальным по критерию максимального значения электромагнитного момента. Этот момент – при управлении c учетом нелинейности кривой намагничивания магнитопровода – будет определяться формулой
![]()
При управлении c учетом нелинейности магнитопровода асинхронного двигателя значения токов, которые обеспечат максимальный электромагнитный момент, не могут быть вычислены аналитически, т. к. функция ψdq(id) является нелинейной. В этом случае целесообразна аппроксимация потока ψdq(id).
Как уже отмечалось выше, магнитный поток ψdq(id) является нелинейной функцией от тока намагничивания. Аппроксимации кривых намагничивания различных видов сталей и магнитопроводов посвящено большое количество работ [9, 10]. В данной статье для описания зависимости ψdq(id) используются следующие функции:
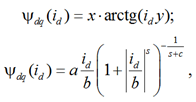
где x, y, a, b, c, s – коэффициенты аппроксимирующих функций.
В первой аппроксимирующей функции используется функция арктангенса, данная аппроксимирующая функция является одной из самых распространенных. Вторая аппроксимирующая функция является модернизацией функции, ранее выведенной одним из авторов статьи [7]. Данная функция позволяет легко манипулировать масштабом и формой кривой намагничивания магнитопроводов электрических машин, а также сталей. Назовем эту функцию степенной аппроксимирующей функцией. На рис. 1 представлены графики аппроксимирующих функций.
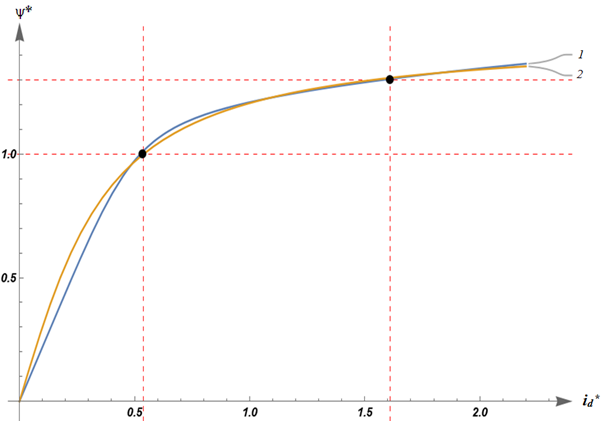
Рис. 1. Графики аппроксимирующих функций: 1 – кривая при аппроксимации степенной функцией;
2 – кривая при аппроксимации функцией арктангенса
Fig. 1. Graphs of approximating functions: 1 − is a curve approximated by a power function;
2 − is a curve approximated by the arctangent function
Потери мощности
Очевидно, управление асинхронным двигателем с максимальным моментом ведет к дополнительным потерям и нагреву, т. к. двигатель работает в режиме перегрузки. В связи с этим работа с таким управлением ограничена по времени. Рассчитать потери в асинхронном двигателе приближенно можно по формуле
![]()
где Rd – сопротивление контура намагничивания статора; Rq – электрическое сопротивление обмотки статора.
Рассмотрим управление электромагнитным моментом при ограничении вектора модуля тока на примере электродвигателя со следующими параметрами, заданными в относительных единицах: ![]() Ограничение, наложенное на ток статора со стороны преобразователя
Ограничение, наложенное на ток статора со стороны преобразователя ![]()
При алгоритме с постоянным номинальным током намагничивания максимальный ток нагрузки с учетом ограничения на модуль тока будет равен:
![]()
Момент, соответственно, равен:
![]()
При алгоритмах управления, учитывающих реальную кривую намагничивания магнитопровода для определения максимального электромагнитного момента, как указывалось выше, необходимо решить уравнение
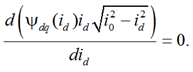
Решить такое уравнение можно только численными методами. В работе для вычислений использовалась система математической алгебры Wolfram Mathematica. Решения с разными аппроксимирующими функциями, рассмотренными выше, представлены в таблице. Полученные результаты приведены в относительных единицах.
Значения переменных асинхронного электродвигателя при использовании
для расчета различных аппроксимирующих функций
The values of an asynchronous electric motor variables when used to calculate various approximating functions
|
Вид аппроксимирующей функции |
Оптимальные значения токов намагничивания и нагрузки |
М*max |
Мmax / Мном |
ΔP* |
|
Аппроксимация с помощью функции, |
1,106 |
1,444 |
0,064 |
|
|
Аппроксимация с помощью функции |
1,083 |
1,423 |
0,063 |
|
|
При |
0,963 |
1,265 |
0,055 |
Согласно вычислениям, учет нелинейности при максимизации электромагнитного момента позволяет существенно повысить точность результата расчета. Следует отметить, что для максимизации электромагнитного момента двигатель необходимо перенасыщать. Потери мощности при насыщении увеличиваются в первую очередь за счет магнитный потерь. Увеличение мощности потерь не является критическим, т. к. при таком управлении предполагается, что двигатель будет работать кратковременно. На рис. 2 представлена механическая характеристика электропривода с учетом полученных вычислений.
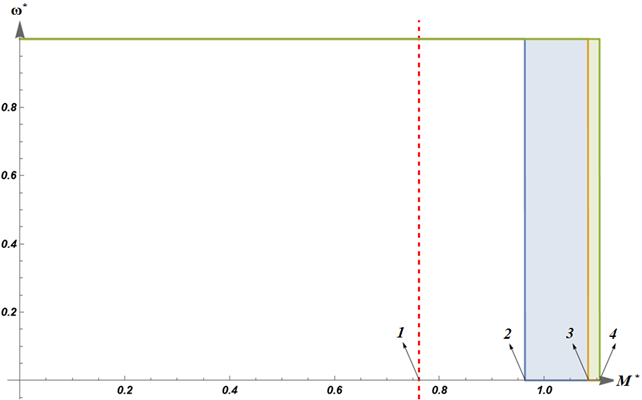
Рис. 2. Механическая характеристика асинхронного двигателя при векторном управлении и максимизации момента:
1 – номинальный электромагнитный момент двигателя; 2 – максимальный электромагнитный момент
при управлении двигателя с постоянным номинальным током намагничивания;
3 – максимальный электромагнитный момент при аппроксимации кривой намагничивания функцией арктангенса;
4 – максимальный электромагнитный момент при аппроксимации кривой намагничивания степенной функцией
Fig. 2. Mechanical characteristics of an asynchronous motor with vector control and torque maximization:
1 – rated electromagnetic torque of the motor; 2 – the maximum electromagnetic torque when driving a motor with
a constant nominal magnetization current; 3 – the maximum electromagnetic moment when approximating
the magnetization curve by the arctangent function; 4 – the maximum electromagnetic moment when approximating
the magnetization curve by a power function
Согласно рис. 2 оптимальный алгоритм управления асинхронным двигателем по критерию максимума электромагнитного момента позволяет расширить его механическую характеристику, тем самым расширив возможности привода и его применения. При этом для реализации предложенного алгоритма не требуется никаких финансовых вложений, достаточно только изменить программу управления приводом.
Выводы
- Максимальный электромагнитный момент асинхронного двигателя достигается при учете нелинейности намагничивания магнитопровода.
- Для учета нелинейности намагничивания магнитопровода целесообразно использовать аппроксимирующие функции. Наиболее распространенными функциями являются тригонометрические функции: арктангенса, гиперболического тангенса, гиперболического синуса и т. д. Авторами статьи рекомендуется использовать выведенную ими степенную функцию.
- Работа двигателя с максимальным электромагнитным моментом возможна в кратковременном режиме, т. к. при таком режиме двигатель работает с перенасыщением магнитной системы, что ведет к его дополнительному перегреву.
- Максимизация электромагнитного момента асинхронного двигателя позволяет расширить его механическую характеристику, а также электропривода в целом. Данный алгоритм управления позволяет получить максимум электромагнитного момента при ограничениях на модуль тока статора со стороны преобразователя энергии.
- Для применения предлагаемого алгоритма максимизации электромагнитного момента асинхронного двигателя не требуется материальных затрат. Для его реализации достаточно изменить программу микроконтроллера, который осуществляет управление электроприводом.
1. Belousov I. V., Gel'ver F. A., Samoseiko V. F., Khomiak V. A. Shirotno-impul'snye preobrazovateli elektricheskoi energii: monografiia [Pulse-width converters of electric energy: monograph]. Saint Petersburg, Izdanie Krylovskogo gosudarstvennogo nauchnogo tsentra, 2019. 231 p.
2. Umiarov D. V., Onishchenko G. B. Kaskadnye preobrazovateli chastoty v sistemakh elektrodvizheniia sudov [Cascade frequency converters in ship electric propulsion systems]. Trudy Krylovskogo gosudarstvennogo nauchnogo tsentra, 2019, no. 4 (390), pp. 163-175.
3. Koptiaev E. N., Evseev R. I., Balashevich V. M. Sistema elektrodvizheniia sudov na baze matrichnogo neposredstvennogo preobrazovatelia chastoty [Ship electric propulsion system based on a matrix direct frequency converter]. Vestnik evraziiskoi nauki, 2015, no. 2 (27), pp. 1-13.
4. Burdasov B. K., Nesterov S. A., Fedotov Iu. B. Preobrazovateli chastoty dlia vysokovol'tnykh elektroprivodov peremennogo toka [Frequency converters for high-voltage AC electric drives]. APRIORI. Seriia: Estestvennye i tekhnicheskie nauki, 2015, no. 4, pp. 1-15.
5. Samoseiko V. F. Teoreticheskie osnovy upravleniia elektroprivodom [Theoretical foundations of electric drive control]. Saint Petersburg, Elmor Publ., 2007. 464 p.
6. Firago B. I., Vasil'ev D. S. K voprosu vektornogo upravleniia asinkhronnymi dvigateliami [On the issue of vector control of asynchronous motors]. Energetika. Izvestiia vysshikh uchebnykh zavedenii i energeticheskikh ob"edinenii SNG, 2015, no. 5, pp. 1-12.
7. Samoseiko V. F., Belousov I. V., Gel'ver F. A., Khomiak V. A. Algoritmy upravleniia elektricheskimi mashinami: monografiia. Vol. 1. Algoritmy upravleniia asinkhronnoi elektricheskoi mashinoi. Saint Petersburg, Izdanie Krylovskogo gosudarstvennogo nauchnogo tsentra, 2020. 116 p.
8. Kulaev N. A., Zubkov P. S., Dubov N. V., Artamonov V. Iu. Uchet namagnichivaniia asinkhronnoi mashiny pri energooptimal'nom upravlenii [Taking into account the magnetization of an asynchronous machine with energy-optimal control]. Inzhenernyi vestnik Dona, 2020, no. 6 (66), p. 12.
9. Belkina E. N., Zhukov A. S. Analiz sposobov approksimatsii krivoi namagnichivaniia elektrotekhnicheskoi stali [Analysis of methods for approximating the magnetization curve of electrical steel]. Innovatsionnaia nauka, 2015, no. 5-2, pp. 22-27.
10. Kas'ianenko M. G., Matiukhov V. F., Vaganov M. A. Approksimatsiia krivykh namagnichivaniia elektrotekhnicheskikh stalei pri proektirovanii elektricheskikh mashi [Approximation of magnetization curves of electrical steels in the design of electrical machines]. Izvestiia SPbGETU «LETI», 2018, no. 9, pp. 69-74.

















