Russian Federation
UDC 520.9
The objective possibility of difficulties in the use of global satellite navigation systems is considered and their negative impact on navigation safety is investigated. An objective increase in the place and role of nautical astronomy in ensuring the navigational safety of navigation in modern conditions is justified. The factors influencing the accuracy of astronomical observations are considered, and an a priori assessment of their accuracy is made, including the currently existing means and methods for calculating the coordinates of the luminaries. The influence of the accuracy of calculating the coordinates of the luminaries on the accuracy of astronomical observations in general is estimated. It is shown that the means and methods of nautical astronomy currently available on ships of the fleet do not allow fulfilling the requirements of IMO Resolution A.1046 to ensure the necessary accuracy of navigation. The need for legislative consolidation of requirements for the accuracy of navigation in the absence of signals from global satellite navigation systems is indicated. It is proposed to use IMO Resolution A.529. The possibility and urgent need for the development and introduction into navigation practice of automated astrogation systems based on new principles of measurement and processing of astrogation parameters are outlined, which will dramatically increase both the accuracy of astronomical observations and the probability of their implementation. It is proposed to use the experience gained in the Russian Navy in the creation and application of such systems. It is proved that the currently available software products for automated calculation of the coordinates of the luminaries can be used in the software of such systems.
means and methods for calculating the coordinates of luminaries, errors in astronomical observation, errors in calculating the coordinates of luminaries, accuracy of navigation when using nautical astronomy, promising direction for the development of nautical astronomy
Введение
Последние десятилетия развитие судовождения связано в первую очередь со спутниковой навигацией. При всех несомненных достоинствах спутниковой навигации это привело к тому, что выведены из эксплуатации или законсервированы большинство наземных радионавигационных систем (РНС), круговых и секторных радиомаяков, на многих судах демонтированы либо вообще не устанавливаются радиопеленгаторы и приемная аппаратура РНС.
Вместе с тем опыт использования глобальных навигационных спутниковых систем (ГНСС), особенно за последнее время, показал резкое возрастание вероятности как отключения такого рода систем над определенной территорией, так и выхода их из строя в целом, особенно в предвоенный или военный период. Совершенно очевидно, что это может привести к очень серьезным последствиям в обеспечении навигационной безопасности судовождения, поскольку других дублирующих средств навигации на борту современных судов практически нет.
В вышеобозначенных условиях резко возрастают место и роль мореходной астрономии как абсолютно автономного средства навигации, пригодного для использования в любом районе Мирового океана. Поэтому совершенствование существующих и разработка новых средств и методов мореходной астрономии являются актуальными научно-техническими задачами.
Новизна работы заключается в априорной оценке существующих средств и методов вычисления координат светил и их влияния на точность астрономической обсервации. Пути решения обозначенных задач обусловлены повышением точности астрономических обсерваций и вероятностью их выполнения в любых условиях плавания.
Целью данной работы является оценка влияния существующих в настоящее время средств и методов вычисления координат светил на точность астрономической обсервации.
Анализ существующих в настоящее время средств и методов вычисления координат светил и их точности
Вычисления экваториальных координат светил, к которым относятся прямое восхождение, гринвичский часовой угол и склонение светил, в настоящее время производятся на судне либо по астронавигационным пособиям, либо с помощью средств вычислительной техники. Для разработки таких астронавигационных пособий или для составления электронных программ необходимо на какую-то начальную дату (астрономическую эпоху) определить наблюдениями с обсерватории координаты светил на небесной сфере, а затем вычислить наперед на какой-то промежуток времени так называемые эфемериды светил [1].
Рассчитанные на определенное время вперед эфемериды светил для целей судовождения публикуются либо в специальных астронавигационных пособиях, либо вводятся в базу данных специальных астронавигационных программ.
К специальным астронавигационным пособиям в отечественном судовождении относятся:
– «Морской астрономический ежегодник» (МАЕ) [2];
– «Морской астрономический альманах» (МАА) [3].
На судах иностранного флота в настоящее время используются следующие астронавигационные пособия:
– британско-американский The Nautical Almanac (NA) [4];
– британский Brown's Nautical Almanac (BNA) [5];
– французский Ephemerides Natiques (EN) [6];
– различные коммерческие копии NA, издаваемые по содержанию NA в различных странах мира.
В целом вышеперечисленные пособия схожи по содержанию. Определенные отличия от всех перечисленных имеет отечественный МАА, издаваемый не ежегодно, а один раз в два года. Применительно к вычислению экваториальных координат светил эти отличия заключаются в том, что:
– значения часовых углов и склонений планет в МАА, в отличие от МАЕ, NA и BNA, даны с шагом в 5 ч, поэтому отличается алгоритм вычисления местного часового угла и склонения планет;
– изменения часовых углов точки Овна и Солнца, звездных дополнений и склонений представлены в МАА в виде медленно меняющейся на двухлетнем интервале целой (градусной) части и быстро меняющейся минутной части;
– в ежедневные таблицы МАА включены видимые места 77 (вместо 63 в МАЕ, 57 в NA и BNA) ярких звезд, что позволяет использовать их без интерполяции.
Развитие вычислительной техники привело к появлению различных электронных программ для решения задач мореходной астрономии. В настоящее время существует достаточно большое количество программ как отечественного, так и зарубежного производства, обеспечивающих в той или иной мере решение задач мореходной астрономии. В качестве примера можно привести отечественные «Электронный альманах МАЕ», «Штурман», PersAY, «Астрономический Альманах» И. Бровина, Astromical Almanac [7], иностранные Skyglobe, Astro.ехе, Scymate PRO и др.
Любая программа, предназначенная для решения задач мореходной астрономии, базируется, прежде всего, на автоматизированном вычислении экваториальных координат светил. Необходимая информация, а именно координаты светил на начальный момент (эпоху), средний наклон эклиптики и другие необходимые данные, представлены в виде электронной базы данных.
Одной из главных проблем при вычислениях эфемерид светил (как при издании астронавигационных пособий, так и при разработке электронных программ) является точность алгоритмов учета явлений прецессии, нутации и годичной аберрации.
Под прецессией в данном случае понимается перемещение полюса мира на сфере вокруг полюса эклиптики и непрерывное наклонение плоскости небесного экватора вследствие влияния сил притяжения Солнца, Луны и планет.
Под нутацией понимается периодическое изменение действующих на Землю сил тяготения Солнца, планет и особенно от Луны, а также их направлений, что вызывает появление более быстрых, как бы колебательных движений полюса мира. Вследствие нутаций координаты всех светил также изменяются.
Под годичной аберрацией понимается смещение луча света от светила в направлении движения Земли вследствие ее годового орбитального движения.
Таким образом, видимые места светил на небесной сфере относительно координатной сетки не остаются постоянными, а подвержены как общим, так и отдельным смещениям.
Общее смещение сетки координат вызывается прецессией и нутацией, движение Земли вызывает аберрацию, а движение Солнечной системы – собственные движения светил.
Собственные движения навигационных звезд ma и md помещены в звездных каталогах и учитываются совместно с прецессией как
∆aпр + ma;
∆dпр + md,
где ∆aпр, ∆dпр – поправки прямого восхождения и склонения за прецессию.
Если прямое восхождение звезды a0 и склонение d0 из каталога (они называются средними) известны на некоторый начальный момент (эпоху), то на любой другой момент ее видимые координаты a, d могут быть рассчитаны по формулам [2]:
a = a0 + (∆aпр + ma)t + ∆aн + ∆aа;
d = d0 + (∆dпр + md)t + ∆dн + ∆dа,
где ∆aн, ∆dн – поправки координат за нутацию; ∆aа, ∆dа – поправки координат за аберрацию; t − промежуток времени от начальной эпохи.
Эти координаты и приводятся в специальных астронавигационных пособиях, предвычисленные на несколько лет вперед.
В настоящее время существуют различные алгоритмы вычисления поправок за прецессию, нутацию и аберрацию [1, 7–9], однако все они не позволяют вычислять эфемериды светил с достаточной для судовождения точностью на достаточно длительный промежуток времени вперед, поскольку требуют периодического уточнения различных астрономических величин. Такое уточнение может быть выполнено только на базе обсерваторных наблюдений, поэтому астронавигационные пособия издаются, как правило, ежегодно, максимум один раз в два года. Такого же периодического обновления, но с более продолжительными интервалами, требуют и большинство электронных программ.
Для вычисления экваториальных координат светил в целях решения задач мореходной астрономии во всех астронавигационных пособиях приведены:
– эфемериды гринвичского часового угла точки Овна на каждый час всемирного координированного времени по Гринвичу в ежедневных таблицах;
– эфемериды звездного дополнения t* и склонения d для 63 в МАЕ, 57 в NA и BNA, 77 в МАА на середину трехсуточного интервала разворота таблиц в разделе «Видимые места звезд» (раздел STARS в NA и BNA) ежедневных таблиц;
– эфемериды звездного дополнения t* и склонения d на первое число каждого месяца для 160 звезд в МАЕ и МАА, для 173 в NA и BNA в отдельной таблице «Видимые места звезд» (таблица STARS в NA и BNA);
– эфемериды гринвичского часового угла и склонения Солнца, Луны и планет на каждый час всемирного координированного времени по Гринвичу (в МАА на каждые 5 ч) в ежедневных таблицах;
– эфемериды прямого восхождения Солнца, Луны и планет на середину трехсуточного интервала разворота таблиц в ежедневных таблицах;
– необходимые поправки для часового угла и склонения точки Овна, Солнца, Луны и планет в «Основных интерполяционных таблицах» (таблицы Increments and corrections в NA и BNA).
Методики вычисления местного часового угла и склонения d [10, 11] при использовании всех вышеперечисленных астронавигационных пособий в целом практически не отличаются друг от друга, за некоторым исключением [11].
Точность вычисления экваториальных координат светил с применением астронавигационных пособий будет зависеть от следующих факторов:
− точности вычисления эфемерид светил, которая в свою очередь будет зависеть от точности обсервационных наблюдений, точности модели звездного каталога, точности алгоритмов вычисления поправок за прецессию, нутацию и годичную аберрацию. В целом влияние этого фактора можно оценить так называемой эфемеридной погрешностью, при этом точность обсервационных наблюдений и точность модели звездного каталога, применяемых при составлении астронавигационных пособий, можно считать приблизительно одинаковыми;
− точности округления вычисленных эфемерид светил. Во всех вышеперечисленных астронавигационных пособиях эфемериды светил приведены с точностью до десятых долей минуты, т. е. погрешность округления в данном случае составит 0,29 единицы последнего знака [12], или 0,029´;
− точности вычисления необходимых поправок для часового угла tгр и склонения d точки Овна, Солнца, Луны и планет;
− точности интерполяции, особенно при вычислениях звездного дополнения t* и склонения d с помощью отдельной таблицы «Видимые места звезд» (таблицы STARS в NA и BNA). Значение погрешности интерполяции можно оценить как 0,23 единицы последнего знака, или 0,023´.
Для навигационных звезд это одна поправка за минуты и секунды при вычислении часового угла. Для Солнца, планет и Луны вследствие неравномерного изменения часового угла и склонения в течение часа добавляются:
– поправка за квазиразность (разницу между фактическим изменением часового угла ближайших к Земле светил за 1 ч среднего времени и наименее возможным его изменением в данном году) при вычислении часового угла;
– поправка за приращение склонения светила за промежуток интерполирования при вычислении склонения.
Значения квазиразностей и приращений склонения приведены в ежедневных таблицах для планет – в последней строке соответствующего столбца, а для Луны на каждый час гринвичского времени (UT).
Методическую погрешность вычисления поправок в данном случае можно принять пренебрежимо малой, а погрешность выборки из таблиц (погрешность округления) составит все те же 0,29 единицы последнего знака, т. е. 0,029´.
Следует отметить, что для Солнца, в отличие от отечественного МАЕ, в NA и BNA значения квазиразностей не приводятся, поэтому при использовании NA или BNA ее значение принимается равным 0. Это снижает точность вычислений часового угла Солнца примерно на 0,1´– 0,2´.
В целом погрешность вычисления экваториальных координат светил с помощью астронавигационных пособий не превышает 0,1´.
Точность вычисления экваториальных координат светил с помощью электронных программ при условии применения одинаковых алгоритмов вычисления поправок за прецессию, нутацию и аберрацию заведомо выше за счет отсутствия погрешностей округления и интерполяции.
Априорное значение погрешности вычисления экваториальных координат светил при использовании электронных программ не превышает 0,05´−0,1´ [7], однако для оценки реальной точности каждой из вышеперечисленных программ требуется отдельное исследование.
Вычисление горизонтных координат светил (счислимых высоты h и азимута А светила) в настоящее время может быть выполнено решением параллактического треугольника следующими способами:
– согласно таблицам логарифмов, приведенным в мореходных таблицах;
– с помощью специальных таблиц;
– посредством вычислительной техники.
Первый способ, ввиду его достаточной трудоемкости, в настоящее время практически не применяется, что подтверждается мнением более чем пятидесяти практикующих судоводителей.
Из достаточно большого количества различных специальных таблиц [10, 11], предназначенных для решения параллактического треугольника, в настоящее время наиболее широкое распространение получили:
– в отечественном флоте: таблицы ТВА-57, приведенные в мореходных таблицах МТ-2000, и таблицы ТВА-52, приведенные непосредственно в МАЕ и МАА;
– в иностранном флоте: таблицы Sight Reduction Tables, приведенные непосредственно в NA.
Точность вычисления счислимых высоты hс и азимута Ас светила с применением таблиц ТВА-57 составляет примерно 0,14´, точность вычисления этих же величин с применением таблиц ТВА-52 несколько хуже (порядка 0,2´–0,3´) за счет дополнительных интерполяций [10].
Точность вычисления счислимой высоты hс светила с применением таблиц Sight Reduction Tables еще хуже (порядка 0,3´–0,5´ в зависимости от диапазона входных аргументов) за счет наличия нескольких интерполяций.
Точность вычисления счислимого азимута Ас светила с применением таблиц Sight Reduction Tables составляет 0,1–0,4° в зависимости от диапазона входных аргументов [11].
Помимо применения рассмотренных выше таблиц, МАЕ, МАА и NA рекомендуют использовать и вычислительную технику, прежде всего микрокалькулятор.
The Nautical Almanac рекомендует использовать для этого традиционные формулы сферической тригонометрии [4]:
sinhс = sinjcsind + cosjccosdcost;
ctgAс = tgdcosjcсоsectм – sinjcctgt,
где t – местный часовой угол светила; d – склонение светила; jc – широта счислимого места судна.
В свою очередь, МАЕ и МАА рекомендуют использовать для этого формулы перехода от параллактического треугольника к двум прямоугольным треугольникам с вычислением дополнительного аргумента х [2, 3]:
tgx = tgδ / cost;
tgAc = tgtcosx / (sin(x ~ φc));
tghc = cosAc / tg(x ~ φc),
где знак ~ (тильда) означает вычисление разности при одноименных φс и х и вычисление суммы при разноименных φс и х.
Точность вычисления счислимых высоты hс и азимута Ас светила с применением вычислительной техники, как правило, не превышает 0,05´.
Оценка влияния погрешностей вычисления координат светил на точность астрономической обсервации
Оценка точности обсервованного места судна радиальной среднеквадратической погрешностью Мо, полученного по небесным светилам способом высотных линий положения при измерениях высот двух светил, может быть произведена с использованием следующих математических зависимостей [13]:
![]()
где mлп1 и mлп2 – среднеквадратические погрешности линий положения; θ – угол пересечения высотных линий положения; r – коэффициент корреляции.
При наличии избыточных измерений судна радиальная среднеквадратическая погрешностью Мо может быть произведена с использованием следующих математических зависимостей [13]:
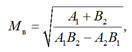
где А1, В1, А2, В2 – коэффициенты при неизвестных системы двух нормальных уравнений метода наименьших квадратов.
Эти коэффициенты, в свою очередь, рассчитываются по следующим формулам:
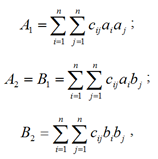
где сi – коэффициент, зависящий от степени корреляции и среднеквадратических погрешностей линий положения mлп1 и mлп2; аi = cosАi, bi = sinАi, аj = cosАj, bj = sinАj – коэффициенты уравнений линий положения.
Поскольку элементами высотной линии положения являются счислимый азимут светила Ас и перенос h-hc, то погрешность собственно высотных линий положения mлп будет определяться погрешностью:
– счислимого азимута светила mА;
– счислимой высоты светила mhc;
– определения истинной высоты светила mh.
Погрешность в вычислении счислимого азимута светила mА, особенно при графической прокладке высотных линий положения, существенного влияния на точность места не оказывает.
Погрешность счислимой высоты светила mhc будет определяться погрешностью рассмотренных выше применяемых для этого средств и погрешностью фиксации момента времени при измерениях высот светил mht.
Среднеквадратическая погрешность вычисления счислимой высоты светила mhc в зависимости от комбинации применяемых средства и методов составляет:
– МАЕ, МАА и таблицы ТВА-57: mhc = 0,18´−0,19´;
– МАЕ, МАА и таблицы ТВА-52: mhc = 0,27´−0,28´;
– МАЕ, МАА и вычислительная техника: mhc = = 0,13´−0,14´;
– NA и таблицы Sight Reduction Tables: mhc = 0,31´;
– NA и вычислительная техника: mhc = 0,13´;
– вычислительная техника (электронная программа): mhc = 0,05´.
Погрешность фиксации момента времени при измерениях высот светил mht (с учетом среднеквадратической погрешности измерения времени mt = 0,5 с):
mht = 0,25´/ сosφsinAmt.
Значение mht в зависимости от широты, азимута и промежутка времени, прошедшего с момента определения поправки рабочих, находится в пределах mht = 0,06´–2,0´.
Погрешность определения истинной высоты светила mh определяется оценкой погрешностей каждой из величин, учитываемой при получении значения h:
h = OCср + (i + s) + ∆hd + ∆hρ + ∆ht + ∆hв + ∆hp ± R,
где OCср – среднее из серии значение измерений отсчета секстана ОС; i – поправка индекса секстана; s – инструментальная поправка секстана; ∆hd – поправка за наклонение видимого горизонта; ∆hρ – поправка за астрономическую рефракцию; ∆ht – поправка за температуру воздуха; ∆hв – поправка за давление воздуха; ∆hp – поправка за параллакс светила; R – поправки за радиус светила.
Поскольку высота светила, как правило, измеряется 3–5 раз, то среднеквадратическая погрешность среднего значения из серии измерений ОС:
![]() ,
,
где mОС – среднеквадратическая погрешность единичного измерения высоты светила; n – количество измерений высоты светила.
Погрешность единичного измерения высоты светила mОС зависит главным образом:
– от умения и искусства судоводителя работать с навигационным секстаном;
– погрешности снятия отсчета со шкалы угломерного микрометрического устройства;
– воздействия качки;
– отклонения секстана от вертикала светила в момент измерения высоты;
– резкости видимого горизонта.
Умение судоводителя работать с навигационным секстаном можно оценить так называемой личной, или субъективной, погрешностью, которую в зависимости от его навыков можно оценить в пределах 0,3´–1,0´.
Погрешность снятия отсчета со шкалы угломерного микрометрического устройства лежит в пределах 0,1´–0,2´.
Погрешность, обусловленная воздействием качки, находится в пределах 0–0,3´.
Погрешность, обусловленная отклонением секстана от вертикала светила в момент измерения высоты, лежит в пределах 0,1´–0,5´.
Погрешность, обусловленная резкостью видимого горизонта, – в пределах 0,2´–0,9´.
Таким образом среднеквадратическая погрешность единичного измерения высоты светила mОС может находиться в достаточно широких пределах – mОС = 0,5´–1,3´ – в зависимости от умений судоводителя и условий наблюдений.
Погрешность определения поправки индекса при условии правильно выполненных выверок навигационного секстана в зависимости от способа определения составляет mi = 0,1´–0,4´.
Инструментальная поправка секстана s определяется в заводских или лабораторных условиях с погрешностью ms = 0,2´–1,5´.
Таким образом, погрешность собственно секстана как измерительного инструмента можно определить как
![]()
Поправки ∆hρ, ∆hp выбираются из таблиц поправок без интерполяции. Поправки приведены с точностью до десятых долей минуты, т. е. погрешность округления в данном случае составит 0,29 единицы последнего знака, т. е. 0,029´. Поправки ∆ht и ∆hв выбираются из таблиц поправок с интерполяцией, следовательно, добавится погрешность интерполяции в 0,23 единицы последнего знака, т. е. 0,023´.
Поправка за наклонение видимого горизонта ∆hd при измерении ее наклономером имеет среднеквадратическую погрешность md = 0,2´, а при выборке ее из таблиц md = 0,4´–2,0´.
Таким образом, априорная среднеквадратическая погрешность высотной линии положения определится путем среднеквадратического сложения составляющих ее элементов:

С учетом рассмотренных погрешностей высотной линии положения априорное значение радиальной среднеквадратической погрешности астрономической обсервации может составить от 0,9 до 6,5 миль в зависимости от количества линий положения, углов их пересечения, условий наблюдения, подготовки судоводителя и используемых для вычисления координат светил средств и методов.
Результаты исследования
1. Погрешность вычисления экваториальных координат светил с применением МАЕ, МАА и NA, а тем более с применением электронных программ, не оказывает существенного влияния на точность астрономической обсервации.
2. Погрешность вычисления горизонтных координат светил зависит от используемого средства вычисления. Наиболее предпочтительным является применение таблиц ТВА-52, ТВА-57 или средств вычислительной техники. Полученная при этом погрешность вычисления также не оказывает существенного влияния на точность астрономической обсервации.
3. Применять для вычисления горизонтных координат светил рекомендуемые NA таблицы Sight Reduction Tables следует только при отсутствии возможностей применения таблиц ТВА-52, ТВА-57 или средств вычислительной техники.
4. Основные погрешности при астрономической обсервации связаны с погрешностями навигационного секстана как измерительного инструмента и погрешностями, обусловленными подготовкой судоводителя и условиями окружающей среды в процессе измерения высот светил.
5. Точность астрономической обсервации, выполненной с применением рассмотренных средств и методов мореходной астрономии, не позволяет выполнить требований к точности судовождения, регламентированных Резолюцией ИМО А.1046 (100 м в открытом море с вероятностью 0,95) [14].
6. Представляется разумным при использовании мореходной астрономии при выходе по каким-то причинам из строя ГНСС вспомнить о требованиях Резолюции ИМО А.529 (4 мили в открытом море с вероятностью 0,95) [15], поскольку они позволяют оценить безопасность судовождения без применения глобальных спутниковых радионавигационных систем.
Заключение
Очевидное усиление роли мореходной астрономии в обеспечении навигационной безопасности судовождения требует принятия необходимых мер по повышению точности и надежности астрономических обсерваций:
− увеличение времени, отводимого на изучение дисциплины «Мореходная астрономия» в морских учебных заведениях с уклоном на практическую отработку измерений астронавигационных параметров;
− ужесточение требований к судоводительскому составу в умении практически производить обсервации по небесным светилам;
− разработка и внедрение в практику судовождения измерительных устройств, позволяющих измерять не только высоту светила, но и другие астронавигационные параметры, такие как азимут светила, разность высот светил, разность азимутов и т. д., в автоматизированном режиме. Следует отметить, что колоссальный опыт разработки и эксплуатации такого рода устройств накоплен в отечественном военно-морском флоте [16];
− разработка и внедрение в практику судовождения астронавигационных систем, позволяющих полностью автоматизировать весь процесс астрономической обсервации от подбора светил для наблюдений до оценки ее точности;
− разработанные к настоящему времени электронные программы вычисления экваториальных и горизонтных координат светил вполне могут быть использованы как часть математического обеспечения таких систем.
1. Abalkin V. K. Osnovy efemeridnoi astronomii [The basics of ephemeris astronomy]. Moscow, Nauka Publ., 2020. 448 p.
2. Morskoi astronomicheskii ezhegodnik – 2020 [Marine Astronomical Yearbook 2020]. Saint Petersburg, Izd-vo IPA RAN, 2019. 336 p.
3. Morskoi astronomicheskii al'manakh (2019–2020) [Marine Astronomical Almanac (2019-2020)]. Saint Petersburg, Izd-vo IPA RAN, 2018. 392 p.
4. The Nautical Almanac 2020. Taunton, The United Kingdom hydrographic office, 2019. 317 p.
5. Brown's Nautical Almanac 2020. Glasgowo, Brown, Son & Ferguson, Ltd., 2019. 1053 p.
6. Ephemerides Natiques 2020. Paris, Bureau des Longitudes, 2019. 496 p.
7. Kozin S. V., Denisova A. A., Altsibeev G. O. Matematicheskaia model' dvizheniia navigatsionnykh svetil na nebesnoi sfere [A mathematical model of the movement of navigational luminaries on the celestial sphere]. Vestnik gosudarstvennogo universiteta morskogo i rechnogo flota imeni S. O. Makarova, 2020, vol. 12, no. 1, pp. 35-45.
8. Krasavtsev B. I. Morekhodnaia astronomiia: uchebnik [Nautical Astronomy: textbook]. Moscow, Transport Publ., 1986. 256 p.
9. Duffett-Smith P. Practical astronomy with your calculator. Cambridge University Press, 1979. 185 p. (Daffet-Smit P. Prakticheskaia astronomiia s kal'kuliatorom / per. s angl. D. A. Ptitsyna, N. E. Piskunova. M.: Mir, 1982. 175 s.).
10. Kirillov N. O. Morekhodnaia astronomiia [Nautical astronomy]. Kaliningrad, Izd-vo BGARF, 2010. 390 p.
11. Kirillov N. O. Reshenie zadach morekhodnoi astronomii s pomoshch'iu inostrannykh astronavigatsionnykh posobii [Solving problems of nautical astronomy with the help of foreign astrogation manuals]. Kaliningrad, Izd-vo BGARF, 2018. 162 p.
12. Kirillov N. O. Opredelenie mesta sudna, otsenka ego tochnosti i navigatsionnoi bezopasnosti plavaniia [Determining the location of the vessel, assessing its accuracy and navigational safety of navigation]. Kaliningrad, Izd-vo BGARF, 2012. 198 p.
13. Morekhodnye tablitsy MT-2000 [Nautical tables MT-2000]. Saint Petersburg, GUNiO MO RF, 2000. 575 p.
14. Resolution A.1046(27). Wordwide radionavigation System. Available at: http//www.info.org/knowledge-Center/IndtfoxoffResolutions/Documents/A%20-%20Assemblv/1046(27)/pdf (accessed: 15.01.2024).
15. Trebovaniia k tochnosti opredeleniia koordinat mesta sudna [Requirements for the accuracy of determining the coordinates of the vessel's location]. Available at: http//seasprint.ru/navigator/navigation/trebovaniya-k-tochnosti-opredeleniya-koordinat-mesta-sudna (accessed: 15.01.2024).
16. Kostin V. N. Istoriia razvitiia otechestvennykh morskikh astronavigatsionnykh sistem [The history of the devel-opment of domestic marine astrogation systems]. Navigatsiia i gidrografiia, 2000, no. 11, pp. 133-137.

















