Russian Federation
Russian Federation
This work is devoted to studying the possibilities of using process analytics methods (Process Mining) to analyze student activity based on digital traces that students leave in learning management systems (LMS). This work examines the specifics of process mining algorithms that can be used to analyze educational processes, namely, heuristic and inductive algorithms are considered as the most effective for building models and suitable for use for the purpose of analyzing educational data. The work involved creating a way to use process analytics algorithms to identify clusters of students with similar behavior patterns. The development of a process analysis algorithm was carried out on the basis of the event log of the distance learning system of Kostroma State University. As a result of the work, models of student behavior were built and visualized, including the identification and clustering of students with similar behavior, the construction of heuristic networks, Petri nets, a direct sequence graph, a BPMN model and a decision tree. An analysis of the resulting models was carried out, which showed that the developed method makes it possible to study the behavioral patterns of students. The proposed method of using intellectual analysis of educational processes can be used to solve issues of increasing the productivity of the educational process, early detection of problems, especially in the context of changing student behavior in the system, as well as the development and optimization of educational programs. In addition, the limitations of this system have been identified, which may hinder its implementation and application in the educational environment of universities.
intellectual analysis, student behavior, educational process, educational program, digital footprint
Введение
Процесс освоения студентом образовательных программ в высшем учебном заведении подразумевает необходимость обеспечения формирования всех обязательных компетенций, предусмотренных Федеральным государственным образовательным стандартом (ФГОС). Обучаясь в вузе, студент должен освоить образовательную программу в полной мере, однако очень часто у студентов навыки формируются непоследовательно и не полностью: например, изучение некоторых дисциплин и модулей может быть сопряжено с серьезными сложностями для студента, препятствующими освоению образовательной программы. В том числе это может быть связано с выбором неподходящего направления подготовки. Кроме того, внедрение дистанционного и смешанного форматов обучения также меняют процесс обучения и усложняют его. В результате мотивация студента падает, что впоследствии приводит к низким результатам и неудовлетворенности студента результатами обучения и качеством образования. Все это обуславливает необходимость перестраивания образовательного процесса.
Данную проблему можно решить через систему сопровождения и поддержки, которая, исходя из выявленных склонностей студента и анализа его работы при получении образовательных результатов, могла бы рекомендовать ему способы организации его образовательного процесса. Создание и внедрение подобной системы сопровождения возможно при наличии в системе управления обучением данных о действиях студентов в процессе обучения, т. е. цифрового следа. Существующие методы анализа данных позволяют изучить характерные черты поведения студентов, учитывать их собственные приоритеты, а также сформировать ожидания о будущей успеваемости студента и осуществить поддержку при организации процесса обучения [1, 2]. Система сопровождения, использующая цифровые следы, может помочь решить задачи выбора наиболее подходящей траектории развития обучающегося в соответствии с выявленными паттернами его поведения в информационной среде [3]. Помимо этого с помощью анализа цифрового следа можно проанализировать накопленные ранее данные о деятельности студента, выявить типовые шаблоны его поведения и сравнить полученные данные с его текущей деятельностью [4]. Данная задача представляет наибольший интерес при анализе деятельности студента, и, как правило, ее решение осуществляется с помощью методов так называемой процессной аналитики (Process Mining). Собирая и анализируя данные образовательного процесса, можно получить информацию о том, как студенты выполняют задания, как часто они обращаются к материалам курса и как они взаимодействуют с преподавателями. Эти данные могут найти применение при оптимизации курсов, адаптации образовательных программ и поддержки процесса обучения.
Методы процессной аналитики
Анализ данных цифровых следов, которые хранятся в системах управления обучением в виде журналов событий, осуществляется при помощи методов процессной аналитики, или интеллектуального анализа процессов (Process Mining) [5]. Интеллектуальный анализ образовательных процессов предназначен для обнаружения актуальной и релевантной информации из образовательных данных [6]. Основная цель интеллектуального анализа образовательных процессов заключается в извлечении знаний из журналов событий, которые записываются при каждом действии пользователя в образовательной системе [7], а также в поиске и сравнении поведенческих паттернов, присущих определенным группам учащихся [8].
Интеллектуальный анализ процессов основан на изучении журналов событий электронных систем управления обучением и других инструментов дистанционного и смешанного обучения [9, 10]. Журнал хранит данные о действиях пользователей, выполненных задачах и временных отметках. В журнале могут содержаться данные о поведении студента на протяжении нескольких семестров; поведение этого студента с течением времени, записанное в системе, называют следом, или трассировкой (trace) [11].
После создания и сбора журналов событий применяются алгоритмы интеллектуального обнаружения и анализа процессов для построения моделей поведения учащихся. Для этого часто используются популярные алгоритмы процессной аналитики – так, в рамках данной работы выбраны эвристический (Heuristic Miner) и индуктивный алгоритмы (Inductive Miner). Эти алгоритмы основаны на модели сетей Петри [12].
Эвристический алгоритм Вейтерса [13] учитывает, насколько часто встречаются события в журнале [13, 14], и применяет фильтрацию для уменьшения шума, удаления неполных данных, низкочастотных событий [15]. Эвристический алгоритм использует граф непосредственного следования, чтобы выявить и отобразить процессы на основе данных из журнала событий. Граф непосредственного следования G(L) журнала событий L – это ориентированный граф, который соединяет действие A с другим действием B тогда и только тогда, когда действие B происходит в хронологическом порядке сразу после действия A для любого данного случая в соответствующем журнале событий L [16]. Граф непосредственного следования является ориентированным графом, в котором узлы представлены событиями из журнала событий L, а ребра – отношениями непосредственного следования событий. Ребро (a, b) присутствует в графе G(L) тогда и только тогда, когда в L существует некоторый след 〈..., a, b, …〉. Граф отражает отношения непосредственного следования, которые характеризуют случаи следования двух действий друг за другом в рамках одного и того же процесса. Если действия a, b входят в трассировку (след) процесса, они могут быть описаны одним из следующих отношений:
– отношение a > b – эти действия выполнялись последовательно, непосредственно друг за другом в рамках одного случая;
– отношение a → b означает прямую причинно-следственную связь: одно действие следовало за другим, но не наоборот;
– отношение a # b описывает пары, которые не следуют друг за другом напрямую. Между ними нет прямых причинно-следственных связей;
– отношение a || b описывает ситуации, когда одно действие выполняется параллельно с другим;
– отношение a >> b описывает такие действия, которые выполняются последовательно, при этом первая задача выполняется также непосредственно после второй (отношение a >> b предполагает наличие в трассировке последовательности задач вида aba);
– отношение a >>> b также описывает действия, выполняющиеся последовательно, однако не обязательно следующие подряд друг за другом, а между ними могут выполняться другие задачи.
Индуктивный алгоритм также используется для обнаружения моделей процессов из журналов событий и является наиболее современным алгоритмом процессной аналитики [16]. Достоинство данного алгоритма заключается в его гибкости и масштабируемости. Его основным преимуществом перед другими алгоритмами является очень высокий показатель корректности (соответствия журналу) получаемых моделей, чего другие алгоритмы не могут гарантированно обеспечить. Кроме того, этот алгоритм также может работать с неполными и зашумленными журналами событий.
Данный алгоритм основан на разделении журнала событий на фрагменты, называемые сокращениями или разделениями, и на последующем обнаружении сокращений на графе непосредственного следования G(L). Выделяют четыре основных типа сокращений:
– сокращение «исключающее ИЛИ». Такое сокращение группирует события таким образом, что между событиями в отдельных группах нет связей;
– сокращение последовательности группирует события так, что действия между ними имеют прямую связь от предыдущей группы к следующей группе, но не наоборот;
– параллельное сокращение. Данное сокращение группирует действия таким образом, что у каждой группы есть начальное и конечное действия, а действия между группами связаны между собой отношением прямого следования;
– сокращение цикла повторения. Данное сокращение создает две группы: выполнение действия и повторное выполнение действия. Действия в журнале событий из повторного выполнения могут начинаться и заканчиваться только с действиями из части выполнения.
Результаты исследования
В данной работе предлагается способ анализа образовательных данных, основанный на применении методов интеллектуального анализа процессов. Для реализации этих методов необходимо извлечь и подготовить данные цифровых следов, которые будут использованы для дальнейшего анализа. В качестве входных данных был использован журнал событий дистанционного факультативного курса «Кадры для цифровой экономики» для учащихся по программам магистратуры. Курс разработан в системе дистанционного обучения Костромского государственного университета. Журнал событий представляет собой таблицу, которая включает в себя 14 567 строк (записей), каждая из которых содержит информацию о действиях студентов в системе за 2021 и 2022 гг. Данная таблица включает 23 поля (столбца), из которых выделены 5 основных полей, где хранятся данные, которые можно использовать для анализа:
– userid – идентификатор пользователя в системе;
– contextinstanceid – идентификатор объекта, над которым выполнено действие (курс, задание, форма);
– action – тип действия, которое выполнил пользователь с тем или иным объектом (загрузил или обновил ответ на задание, просмотрел блок и т. д.). Принимает значения “assessed”, “created”, “deleted”, “duplicated”, “submitted”, “updated”, “uploaded”, “viewed”;
– target – реакция системы или преподавателя на активность студента (поставлена оценка, оставлен комментарий к работе и т. д.). Может принимать значения “assessable”, “badge_listing”, “comment”, “course”, “course_module”, “course_module_completion”, “course_user_report”, “discussion”, “feedback”, “grade_report”, “submission”;
– timecreated – время действия в UNIX-формате.
Рассмотрим процесс анализа данных.
1. На основе подготовленных данных строится матрица переходов (transition matrix). Матрица переходов используется эвристическим алгоритмом при построении эвристических правил, применяемых для построения модели. Она представляет собой таблицу, содержащую количество переходов между уникальными событиями в системе. Веса переходов позволяют определить, какие переходы являются наиболее значимыми и какие шаги часто сопровождают друг друга в процессе обучения, – иными словами, с помощью матрицы перехода можно выявить причинно-следственные связи между событиями и определить отношения порядка (следования) между ними. На рис. 1 приведен фрагмент полученной матрицы переходов на основе имеющегося журнала событий.
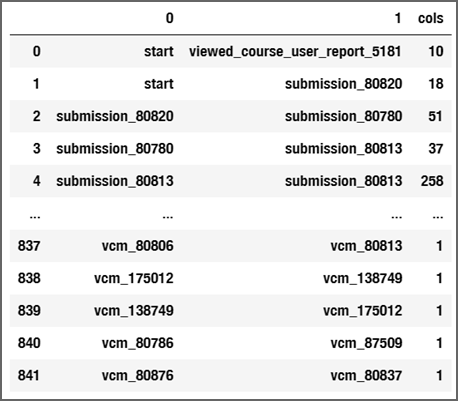
Рис. 1. Матрица переходов
Fig. 1. Transition matrix
2. На следующем этапе строится граф событий. Граф представляет собой сеть событий, где точкой входа является наиболее часто встречающееся событие, относительно которого формируются остальные цепочки событий. Вершинами графа являются действия студентов, которым присваиваются идентификаторы вида «Название действия_Номер действия».
3. Для изучения активности студентов используется построение диаграммы рассеяния (scatter plot). Диаграмма имеет два измерения: по оси x отмечены временные характеристики событий, по оси y – идентификаторы событий. Строки соответствуют конкретному событию в системе. Каждая точка скаттера представляет собой структуру, хранящую данные идентификатора пользователя и его активности.
Диаграмма строится по двум параметрам: относительно даты начала курса (в данном случае, это 1 сентября) и относительно первого входа студента в систему. Для этого по данным из журнала событий вычисляется время (в днях), прошедшее с момента начала курса и с момента первого посещения курса в системе до того или иного события.
4. Диаграмма рассеяния позволяет выявить основные поведенческие паттерны студентов, однако не дает понимания того, есть ли среди студентов группы со схожим поведением, и не позволяет выявить их поведенческие паттерны. Чтобы это выяснить, необходимо выполнить кластеризацию действий студентов и построить процессные модели для выявленных кластеров. Для кластеризации используется модель байесово-гауссовой смеси (Bayesian Gaussian Mixture). Здесь выделяется оптимальное количество кластеров, которые затем отображаются на построенной ранее диаграмме рассеяния.
5. На следующем этапе создается функция, формирующая матрицу, в которой строками являются идентификаторы студентов, а столбцами – вершины графа событий. Значения в таблице состоят из двух параметров: флаг, обозначающий, входит ли данная вершина в граф студента (т. е. выполнял ли он это действие), и принимающий значение 0 и 1, а также количество дней от начала курса до последнего входа в данную вершину. Полученная матрица нормализуется с помощью инструмента MinMaxScaler, используемого для масштабирования признаков в заданном диапазоне. Затем она преобразуется в матрицу косинусных расстояний между действиями студентов путем вычисления парных метрик
с помощью метода pairwise_distances. Для вычисления матрицы выбрана косинусная мера расстояния. В результате получена матрица попарных расстояний, где каждый элемент (i, j) представляет собой расстояние между i-м и j-м объектами.
Далее матрица сжимается в двумерное пространство с помощью двух методов снижения размерности данных – t-SNE и MDS – для формирования кластеров. Эти методы позволяют представить многомерные данные в пространстве меньшей размерности с сохранением их структуры, что упрощает визуальное понимание структуры данных, выявление кластеров, паттернов или выбросов.
6. На последнем этапе выполняется кластеризация полученной матрицы с помощью байесово-гауссовой смеси (Bayesian Gaussian Mixture). Для каждого выделенного кластера применяются следующие модели процессной аналитики для выявления и визуализации поведенческих моделей студентов из каждого кластера:
– эвристический алгоритм (процесс визуализируется в виде эвристической сети и сети Петри);
– граф непосредственного следования;
– индуктивный алгоритм (процесс визуализируется в виде модели BPMN (Business Process Model and Notation) и дерева решений).
В результате применения приведенного алгоритма получен ряд моделей, позволяющих проанализировать поведенческие траектории студентов. Первым полученным визуализатором была диаграмма рассеяния от даты начала курса (в данном случае – от 1 сентября). На рис. 2 представлена полученная диаграмма рассеяния.
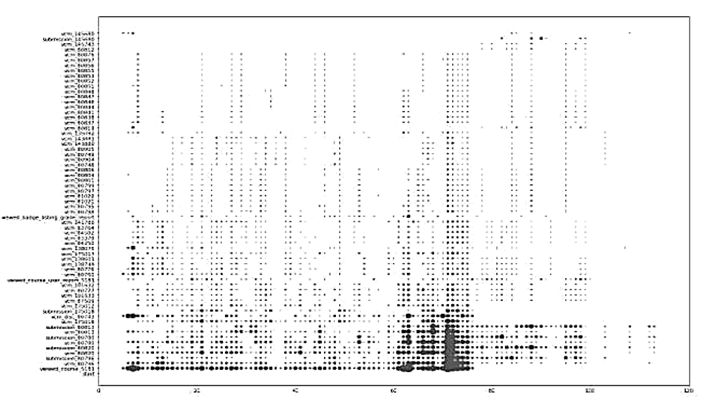
Рис. 2. Диаграмма рассеяния, показывающая распределение активности студентов от 1 сентября
Fig. 2. A scatter chart showing the distribution of student activity from September 1
В диаграмме по оси x отмечено время событий, по оси y – идентификаторы событий. Строки соответствуют конкретному событию в системе. Каждая точка графика представляет собой структуру, хранящую данные идентификатора пользователя и его активности. Данные диаграммы позволяют оценить активность студентов на курсе. Можно заметить, что точки уплотняются, начиная примерно с 70 дня; учитывая, что график построен от 1 сентября, это означает, что всплеск активности наблюдался в ноябре, т. е. ближе к концу семестра. Можно предположить, что это связано с активностью перед сессией, когда большая часть студентов пытается сдать недостающие лабораторные работы и другие задания. От 80 до 120 дня (конец ноября – конец января) наблюдается резкое снижение активности, что может быть связано с окончанием работы в семестре, и активность, наблюдаемая
в этот период, исходит от студентов, которые не смогли закончить работу в течение семестра и закрывали задолженности в период сессии.
На следующем шаге производится масштабирование данных, и после сжатия и повторной кластеризации получено меньшее количество более крупных кластеров студентов со схожими поведенческими паттернами, объединяющими события по их типу и временной метке. Сжатие производилось двумя методами: t-SNE и MDS. На рис. 3 изображены полученные сжатые кластеры активностей от 1 сентября.

Рис. 3. Кластеры активности от 1 сентября после сжатия t-SNE
Fig. 3. Clusters of activity from September 1 after t-SNE compression
Сжатие t-SNE выделило кластеры более четко, поэтому дальнейший анализ будет производиться именно с этими кластерами. Однако на данном этапе нельзя точно оценить поведение студентов, попавших в данные кластеры, поэтому на основании полученных кластеров строятся процессные модели для выявления поведенческих особенностей.
Рассмотрим рис. 3 и для примера возьмем левый кластер. Для выявления особенностей поведения алгоритм строит ряд моделей. В первую очередь строится эвристическая сеть, сеть Петри и DFG-граф. По данным моделям можно определить последовательность выполнения действий. На рис. 4 представлен пример эвристической сети.
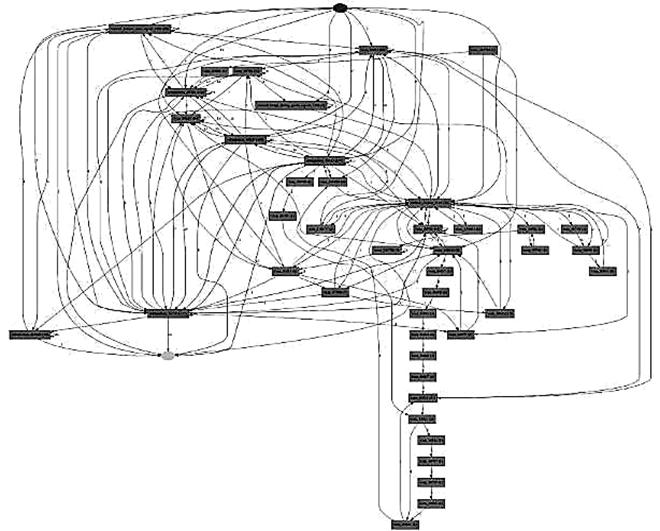
Рис. 4. Пример эвристической сети
Fig. 4. Example of a heuristic network
На данной схеме можно видеть последовательность выполнения действий и активность студентов в системе.
Для более подробного понимания процесса используется индуктивный алгоритм, который визуализирует процесс в нотации модели BPMN. На рис. 5 приведен фрагмент полученного графика.
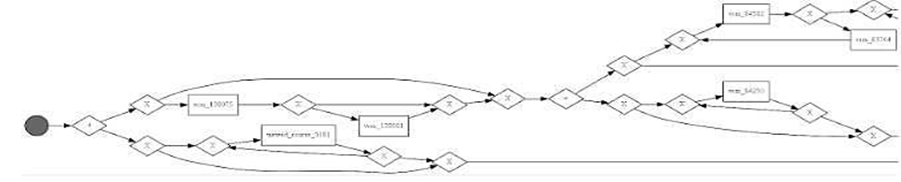
Рис. 5. Фрагмент схемы BPMN
Fig. 5. BPMN diagram fragment
Можно заметить, что студенты, действия которых попали в данный кластер, в первую очередь изучали теоретические онлайн-материалы – это могут быть онлайн-ресурсы, видеолекции, статьи и т. д. Можно также заметить, что в редких случаях встречаются циклы, которые указывают на те случаи, когда студент возвращается к тому или иному элементу курса. Анализ визуализаторов показал, что действия, попавшие в данный кластер, характеризуют линейное изучение курса с последовательным освоением материалов, при этом изучение теоретического материала часто встречается раньше, чем выполнение практических заданий. Это позволяет предположить успешное усвоение курса данными студентами.
На рис. 6 представлен еще один фрагмент данной схемы BPMN, на котором наглядно видна последовательность выполнения действий.

Рис. 6. Фрагмент схемы BPMN с последовательными действиями
Fig. 6. Fragment of BPMN diagram with sequential actions
Далее рассмотрим правый верхний кластер (см. рис. 3). Построение тех же моделей, что и для предыдущего кластера (эвристическая сеть, сеть Петри и граф непосредственного следования), показывает, что модель становится намного сложнее и менее последовательной по сравнению с предыдущим кластером. Активности, связанные с выполнением практических и лабораторных заданий, часто идут до изучения теоретического материала. Схема BPMN данного кластера (рис. 7) наглядно подтверждает гипотезу о том, что данная группа студентов
в первую очередь предпочитает сдавать задания и только в случае неудачи приступает к изучению теоретического материала.
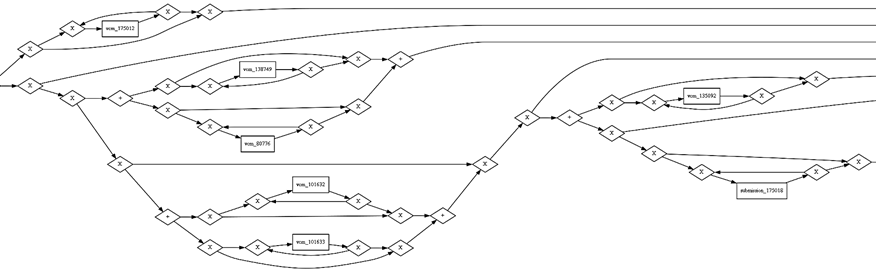
Рис. 7. Фрагмент диаграммы BPMN для второго кластера
Fig. 7. Fragment of BPMN diagram for the second cluster
Кроме того, на данной диаграмме видно множество непоследовательных действий и циклов, когда студент возвращается к предыдущим элементам, предположительно с целью исправления заданий или повторного изучения материала.
Обсуждение
Построенные модели поведения студентов помогают сделать вывод о том, что разработанный алгоритм позволяет изучать шаблоны поведения студентов, выявлять группы студентов, которые испытывают трудности при освоении каких-либо дисциплин, тем или блоков. Данный способ применения интеллектуального анализа образовательных процессов можно использовать для решения следующих вопросов:
– увеличение продуктивности образовательного процесса. Процессная аналитика способна выявить группы студентов, имеющих разную успеваемость и мотивацию, и адаптировать и персонализировать освоение образовательных программ. Приемы процессной аналитики могут выявить оптимальные методики для разных групп обучающихся;
– раннее обнаружение проблем. С помощью процессной аналитики можно выявить привычные паттерны и индивидуальные поведенческие шаблоны студента, а также, что более важно, отследить негативные изменения в этих паттернах. Предложенный инструмент может представлять интерес в контексте отслеживания изменений в поведении студента: резкие перемены могут стать сигналом к будущим проблемам с освоением образовательной программы. Так, если модели поведения того или иного студента показывали успешное освоение курса в определенный период времени, а затем показатели резко снижаются (снижается частота посещения курса, проявляется непоследовательное поведение и т. д.), это может говорить о возникающих сложностях, при этом появляется возможность вовремя отследить эти изменения и принять решение на их основе;
– развитие и оптимизация образовательных программ. Алгоритм даст возможность преподавателям и руководителям образовательных программ оценить и при необходимости пересмотреть образовательные материалы и подходы к изучению тех дисциплин и тем, которые вызывают трудности у студентов (можно изменить количество часов, отредактировать фонд оценочных средств и т. п.).
Заключение
Предложенный метод выявления и оценки поведения различных групп студентов по цифровым следам, оставленным в системах управления обучением, позволил проанализировать поведенческие шаблоны и показал, что разработанный алгоритм может использоваться для принятия решений по управлению поведением студентов. Кроме того, данный инструмент может также показать дисциплины и элементы курса, которые даются студентам сложнее всего и требуют доработки.
Следует, однако, отметить ряд вопросов и проблем, которые могут возникнуть при внедрении подобных методов. Здесь актуальны вопросы автоматизированной обработки разрозненных данных и выбора критериев оценки этих данных. Необходимость анализа больших объемов неоднородных следов в наборах образовательных данных может быть серьезным препятствием, поскольку журналы событий могут содержать огромное количество событий. Кроме того, даже процесс уменьшения сложности обработки данных достаточно сложен
и не всегда автоматизируется. При этом, как показали исследования [17], эффективность подобных систем не превышает 65 %, и анализ поведения студента нельзя осуществить исключительно по данным цифровых следов и онлайн-информации.
Получаемые процессные модели поведения студентов сложны для восприятия: анализ полученных моделей требует от исследователя определенных навыков, которых может не быть у преподавателей. Обучение персонала может стать решением этой проблемы, однако здесь возникают затруднения мотивационного характера: персонал может быть не готов к изучению работы предложенных моделей.
Также существуют специфические особенности обеспечения конфиденциальности исследования. Студенты должны знать, какие данные об их действиях фиксируются и подвергаются анализу. Использование обезличенных данных для аналитики частично решает эту проблему, однако изучение поведения отдельного студента невозможно без его согласия.
Однако даже в том случае, когда система анализа цифрового следа работает достаточно эффективно, она не заменяет преподавателя. Ее роль носит консультативный характер, когда окончательное решение и взаимодействие со студентом остается за преподавателем.
По этим причинам перспективы дальнейшей работы состоят в увеличении точности создаваемых моделей и одновременном упрощении их восприятия, а также в разработке методов улучшения пользовательского опыта для облегчения построения подобных моделей и реализации возможности внедрения данных методов в образовательный процесс.
1. Hachicha W., Ghorbel L., Champagnat R., Zayani C. A., Amous I. Using Process Mining for Learning Resource Rec-ommendation: A Moodle Case Study. Procedia Computer Science, 2021, vol. 192, pp. 853-862. DOI:https://doi.org/10.1016/j.procs.2021.08.088.
2. Wang S., Christensen C., Xu Y., Cui W., Tong R., Shear L. Measuring Chinese Middle School Students’ Motivation Using the Reduced Instructional Materials Motivation Survey (RIMMS): A Validation Study in the Adaptive Learning Setting. Frontiers in Psychology: Menlo Park. Redwood City, Shanghai, 2020. Vol. 11. 8 p. DOI:https://doi.org/10.3389/fpsyg.2020.01803.
3. Popov M. D., Loginova A. A., Denisov A. R. Instrument vyiavleniia patternov povedeniia studentov KGU na osnove algoritmov PROCESS MINING [A tool for identifying patterns of behavior of KSU students based on PROCESS MINING algorithms]. Tekhnologii i kachestvo, 2022, no. 3 (57), pp. 34-38. DOI:https://doi.org/10.34216/2587-6147-2022-3-57-34-38.
4. Vinogradova D. A., Krasavina M. S. Prototipirovanie informatsionnoi sistemy avtomaticheskogo monitoringa motivatsii studentov [Prototyping of an information system for automatic monitoring of student motivation]. Tekhnologii i kachestvo, 2020, no. 3 (49), pp. 25-29. DOI:https://doi.org/10.34216/2587-6147-2020-3-49-25-29.
5. van der Aalst W. M. P. Process mining: Data science in action. Springer, 2016. Pp. 1-477.
6. Şimşek H. Process Mining in Education: Use cases, Pros & Cons in 2024. Available at: https://research.aimultiple.com/process-mining-education/ (accessed: 04.02.2022).
7. Bogarín A., Cerezo R., Romero C. Discovering learning processes using Inductive Miner: A case study with Learning Management Systems (LMSs). Psicothema, 2018, vol. 30, no. 3, pp. 322-329. DOI:https://doi.org/10.7334/psicothema2018.116.
8. Deeva G., Weerdt J. Understanding automated feed-back in learning processes by mining local patterns. Business Process Management Workshops, 2018, pp. 56-68. DOI:https://doi.org/10.1007/978-3-030-11641-5_5.
9. Arpasat P., Premchaiswadi N., Porouhan P., Prem-chaiswadi W. Applying Process Mining to Analyze the Behavior of Learners in Online Courses. International Journal of Information and Education Technology, 2021, vol. 11, no. 10, pp. 436-443. DOI:https://doi.org/10.18178/ijiet.2021.11.10.1547.
10. van der Aalst W. M. P., Guo S., Gorissen P. Com-parative Process Mining in Education: An Approach Based on Process Cubes. IFIP International Federation for Infor-mation Processing, 2015, pp. 110-134. DOI:https://doi.org/10.1007/978-3-662-46436-6_6.
11. Douzali E., Darabi H. A Case Study for the Application of Data and Process Mining in Intervention Program Assessment and Improvement. American Society for Engineering Education, 2016, pp. 1-15.
12. van der Aalst W. M. P., Weijters A. J. M. M., Maruster L. Workflow Mining: Discovering Process Models from Event Logs. IEEE Transactions on Knowledge and Data Engineering, 2004, pp. 1128-1142. DOI:https://doi.org/10.1109/TKDE.2004.47.
13. Weijters A. J. M. M., van der Aalst W. M. P., Alves de Medeiros A. K. Process Mining with the Heuristics Min-er-algorithm. Cirp Annals-manufacturing Technology, 2006, pp. 1-35.
14. Mitsiuk A. A., Shugurov I. S. Sintez modelei protsessov po zhurnalam sobytii s shumom [Synthesis of process models based on event logs with noise]. Modelirovanie i analiz informatsionnykh sistem, 2014, vol. 21, no. 4, pp. 181-198. DOI:https://doi.org/10.18255/1818-1015-2014-4-181-198.
15. Process Mining with Python tutorial: A healthcare application – Part 3. 2020. Available at: https://medium.com/@c3_62722/process-mining-with- python-tutorial-a-healthcare-application-part-3-cc9af986c122 (accessed: 06.04.2021).
16. Leemans S. J. J., Fahland D., van der Aalst W. M. P. Discovering Block-Structured Process Models from Event Logs – A Constructive Approach. Conference: Application and Theory of Petri Nets and Concurrency – 34th International Conference, PETRI NETS 2013 (Milan, Italy, June 24-28, 2013), Proceedings. 2013. Pp. 311-329. DOI:https://doi.org/10.1007/978-3-642-38697-8_17.
17. Romero C., Espejo P. G., Zafra A., Romero J. R., Ventura S. Web Usage Mining for Predicting Final Marks of Students That Use Moodle Courses. Comput. Appl. Eng. Educ., 2013, vol. 21, pp. 135-146. DOI:https://doi.org/10.1002/cae.20456.















