Russian Federation
from 01.01.2023 until now
Russian Federation
The problem of the theory of schedules with an additional condition – the need to choose an alternative chain of operations in the technical processes of products is considered. A two-stage planning algorithm is proposed, the first stage of which is the selection of chains of operations suitable for a certain criterion from the given alterna-tives, after which the task is reduced to the classic JSSP (Job-Shop Scheduling Problem) problem. At the second stage, the selected production operations are arranged on the machines, taking into account the order of the technological process and other restrictions. Minimization of changeover time in production was chosen as an optimization criterion. The description of the algorithm and its implementation is given on the example of the cable industry (production of wiring harnesses). Both stages of planning are implemented on the basis of greedy algorithms, the results of test measurements on various amounts of data (up to tens of thousands of operations) are presented. The implementation is made in C# 10 using a free platform .NET 6. The vector of further research is the implementation of more complex algorithms (in particular, based on evolutionary methods) in order to obtain more optimal plans.
scheduling problems, minimization of setup times, scheduling theory, greedy algorithms
Введение
Эффективное производственное планирование является одним из важнейших факторов успешной деятельности предприятия. Как правило, выделяют три уровня планирования – стратегическое, долгосрочное и оперативное. Каждый из уровней решает свои задачи, при этом план более высокого уровня является преемственным для следующих уровней планирования. Самым детальным этапом планирования является оперативно-календарное планирование, выходом которого являются производственные расписания и сменные задания, которые выдаются конкретным исполнителям. Производственное расписание описывает, в какое время и на каком оборудовании нужно выполнить заданную производственную операцию. Построение производственного расписания является задачей дискретной оптимизации, относящейся к теории расписаний. Большинство задач теории расписаний являются NP-труд-
ными (Nondeterministic Polynomial Time). Существует ряд систем производственного планирования (системы класса APS – Advanced Planning and Scheduling – и MES – Manufacturing Execution System), позволяющих получать эффективные с точки зрения производства планы за приемлемое время.
Задача построения производственного расписания значительно усложняется при наличии ветвлений в технологическом процессе. Классическая постановка задачи производственного планирования не предусматривает наличие каких-либо альтернативных работ и необходимость выбора между ними. Как правило, эта задача решается при планировании на более высоком уровне – долгосрочном. Однако в реальности этап долгосрочного планирования часто игнорируется, например, на производстве отсутствует подходящая система планирования, а стоимость ее внедрения является очень высокой, либо специфика производства достаточно узконаправленная, и имеющиеся системы не подходят для решения такой задачи. В некоторых случаях наличие ветвлений в техпроцессах на этапе оперативного планирования оправдано – в частности, при минимизации производственных переналадок. Данная проблема актуальна в первую очередь для предприятий серийного производства. Для единичного производства проблема менее актуальна, т. к. для изделий обычно сразу определен технологический процесс без ветвлений. Кроме того, альтернативные работы, как правило, определены в рамках конкретных заготовок изделия, наличие которых является характерной чертой дискретного производства, для непрерывного производства технологические процессы имеют меньшую сложность.
На данный момент большинство систем производственного планирования не позволяют планировать альтернативные цепочки операций в техпроцессах [1]. Подходящие системы являются зарубежным программным обеспечением и имеют высокую стоимость внедрения. Таким образом, возникает потребность в импортозамещении зарубежных программных продуктов. Также проблемой является отсутствие актуальных исследований, описывающих методы построения производственных расписаний с учетом альтернативности в техпроцессах.
Основной целью работы является повышение эффективности предприятий за счет внедрения разработанного алгоритма планирования. Для достижения этой цели необходимо выполнить следующие задачи:
– изучить специфику техпроцессов с альтернативными цепочками операций;
– рассмотреть ряд методов, которые можно использовать для построения производственных расписаний;
– разработать алгоритм планирования на основе одного из выбранных методов и произвести его апробацию.
Примеры альтернативности в техпроцессах
Одним из примеров производства, для которого характерно наличие альтернативных цепочек операций, является кабельная промышленность, а именно производство жгутов проводов. Жгут провода состоит из отдельных проводов, которые могут обрабатываться в определенном порядке. Схематичное изображение жгута представлено на рис. 1: пунктирные линии – отдельные провода, на которые ставится контакт (заштрихованный прямоугольник), нарезка и установка контакта каждого провода может происходить параллельно до момента их объединения.
Рис. 1. Схематичное изображение жгута проводов
Fig. 1. Schematic representation of the wiring harness
Каждый провод может обрабатываться параллельно с другими до момента их соединения (армирование или сварка нескольких проводов). Один из видов альтернативных цепочек операций – выполнение различных этапов на разных группах рабочих центров. Например, провод может быть нарезан и заармирован на линии (и это будет считаться одной неделимой работой) или нарезан на одном станке и заармирован на другом (или вручную). Пример подобной вариативности представлен на рис. 2: один и тот же перечень работ (резка и армирование провода) описывается в виде двух последовательностей работ, объединяющихся на этапе сборки.
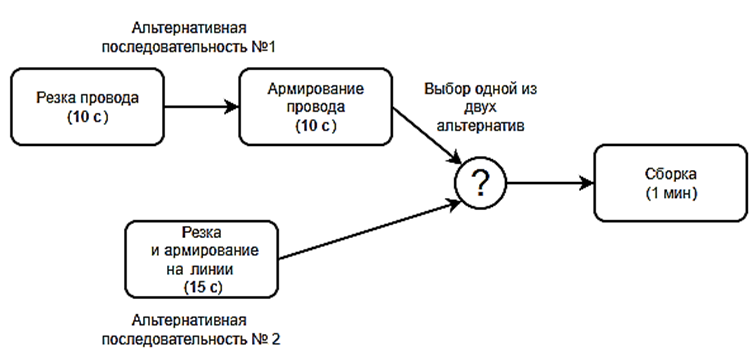
Рис. 2. Пример ветвления в технологическом процессе
Fig. 2. An example of branching in a technological process
Один из способов планирования подобных цепочек – их перенос в отдельные технологические карты. Выбор подходящего варианта изготовления происходит на этапе долгосрочного планирования. Однако этот подход имеет существенный недостаток: необходимо разработать и поддерживать в актуальном состоянии множество технологических карт по каждой из возможных заготовок (в рамках жгута проводов – у каждого провода может быть различное сечение, устанавливаемые контакты и т. д.).
Классификация задачи
Рассматриваемая задача основана на подклассе задач теории расписаний – JSSP (Job-Shop Scheduling Problem) [2]. В рамках этой задачи задано множество работ J = {j1, j2, ..., jN} и машин M = {m1, m2, ..., mM}. Для каждой из работ указано множество операций Oj = {Oj1, Oj2, ..., Ojk}, которые выполняются последовательно. В некоторых случаях для работ указаны связи предшествования Pj, описывающие последовательность выполнения работ.
Возможные критерии оптимальности расписания обычно разделяют на две группы:
– повышение прибыли (например, количество просроченных или выполненных в срок заказов);
– снижение издержек (уменьшение времени простоя оборудования, количества используемых машин, уменьшение суммарной длительности переналадок).
Существует множество различных методов решения задач класса JSSP, которые обычно разделяют на несколько групп:
1. Точные методы (полный перебор, метод ветвей и границ, динамическое программирование). Существуют различные исследования о поиске оптимального расписания для заданного множества машин и работ с использованием переборных алгоритмов [3]. Основной недостаток – их практически невозможно применить в планировании производства из-за очень большого количества производственных операций, которые нужно запланировать за короткое время, т. к. на практике очень часто приходится пересчитывать расписание несколько раз за смену с учетом изменившейся производственной ситуации, а также при сценарном планировании «что будет, если».
2. Метаэвристические методы. К ним относятся в первую очередь различные эволюционные алгоритмы (генетические, муравьиные и т. д.). Они позволяют получить приближенное решение за оптимальное время. Один из недостатков – возможность попадания в локальный оптимум.
3. Правила диспетчеризации и прочие эвристики планирования (как правило, на основе жадных алгоритмов). Основной недостаток заключается в том, что хороший эвристический алгоритм сложно реализовать без знаний предметной области, и зачастую он становится привязан к специфике конкретного производства.
4. Гиперэвристические (hyper-heuristics) методы, в частности генетическое программирование, основная суть которого заключается в генерации эвристических правил без привязки к предметной области [4]. Например, условие выбора следующей операции или наиболее подходящей машины для планирования представляется в виде некоторого выражения или дерева принятия решений, которое кодируется в виде хромосомы и отдается на вход генетического алгоритма.
5. В некоторых случаях при решении задач планирования также применяют методы машинного обучения и искусственные нейронные сети (например, BINN [5] и сети Кохонена [6]). Как правило, их используют при решении некоторых подзадач (например, при распределении операций на машины).
Формальное описание задачи
Задан набор кортежей Orders из n элементов, описывающий параметры каждого производственного заказа Orders = {processi, si, di}. Параметр si описывает директивную дату начала i-го заказа, в то время как di представляет дату его окончания. Элемент processi = {Oi1, ..., Oij} описывает технологический процесс заказа – набор производственных операций. Каждая j-я операция i-го заказа представлена в виде кортежа Oij = {pij, MCij, Altij}, где pij – нормативная длительность операции в секундах (считаем, что длительность операции одинакова при выполнении на различных машинах); MCij описывает набор k альтернативных комбинаций машин, необходимых для выполнения операции, 
, т. е. операция может выполняться на нескольких машинах одновременно (например, основное оборудование и дополнительная оснастка); для описания последовательности альтернативных операций техпроцесса для каждой операции указан набор зависимостей Altij. При этом каждый l-й элемент 
. Для операции «Сборка» из рис. 2
Это означает, что перед выполнением операции «Сборка» нужно принять одно решение – выбрать и запланировать одну из двух заданных операций.
Как и в классической постановке задачи JSSP, задается набор машин M = {m1, m2, ..., mM}. Каждая машина может обрабатывать только одну операцию в момент времени t. Для каждой 
задана функция доступности
описывающая доступность машины согласно графику доступности. Также задана функция расчета переналадок 
, возвращающая длительность переналадки (в секундах) для операции onext на заданной машине m и предыдущей операции oprev, 
, где 
.
Пусть χ – множество возможных расписаний для заданного набора заказов и машин. Критерий оптимизации представлен в виде функции 
– общая длительность переналадки на машине 
для расписания 
. Согласно [7], рассматриваемая задача относится к задачам планирования переналадок с учетом последовательности операций (sequence-dependent setup times). Для расчета длительности переналадок в APS/MES-системах используют матрицы переналадок [8] либо применяют более сложные вычисления, описывающие определенные производственные процессы, такие как остывание или нагрев материала.
Предлагаемое решение
Задачу планирования с альтернативными цепочками операций можно свести к классической задаче планирования, введя этап поиска подходящей альтернативы при каждом выборе операции. Полученный таким способом набор операций 
далее будет называться маршрутом. При изучении специфики техпроцессов предприятий кабельной промышленности была замечена следующая закономерность: альтернативные цепочки операций характерны для первых этапов технологического процесса, при этом именно на этих этапах происходит большее количество переналадок оборудования из-за разнообразия материалов с различными характеристиками (резка проводов разной длины и сечения, установка различных контактов).
Процесс планирования разделяется на 2 этапа – формирование маршрута операций и их планирование на ресурсы с минимизацией производственных переналадок. На первом этапе происходит укрупненное планирование без учета производственных переналадок и формируется маршрут операций. На втором этапе выбранные к планированию операции распределяются на конкретные ресурсы с учетом переналадок и других ограничений.
После сравнительного анализа различных методов планирования в качестве основы для алгоритма планирования были выбраны жадные алгоритмы,
т. к. они позволяют получить приближенное решение за минимальное время, что наиболее актуально при необходимости частого перепланирования.
Блок-схема алгоритма выбора маршрута приведена на рис. 3.
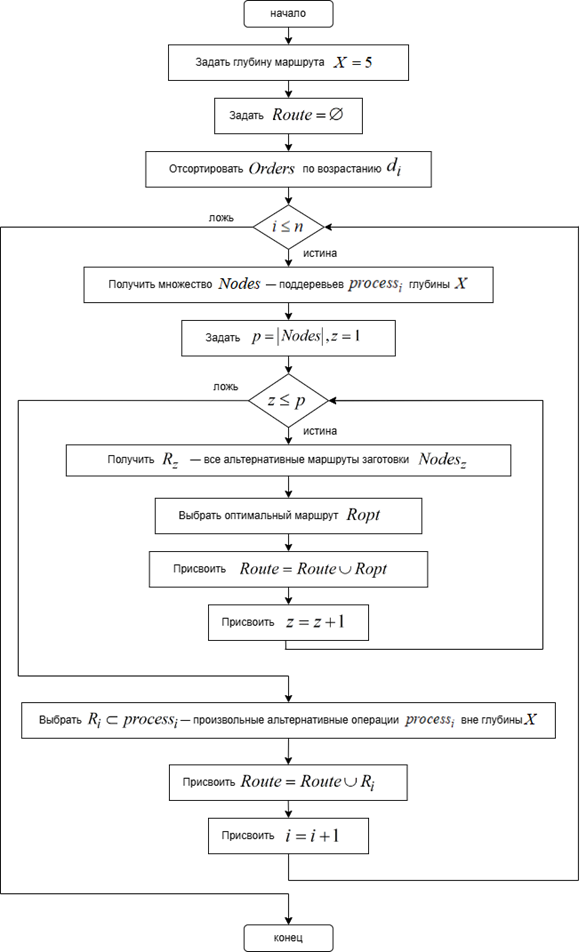
Рис. 3. Блок-схема алгоритма выбора маршрута
Fig. 3. Block diagram of the route selection algorithm
Маршрут Ropt считается оптимальным в том случае, если время окончания последней операции маршрута является минимальным. Операция Oij считается доступной к планированию в том случае, если 
, где 
– количество запланированных операций альтернативы alt, (на втором этапе планирования 
). При выборе операции к планированию из очереди операций удаляются ее возможные альтернативы.
Блок-схема жадного алгоритма с минимизацией переналадок приведена на рис. 4.
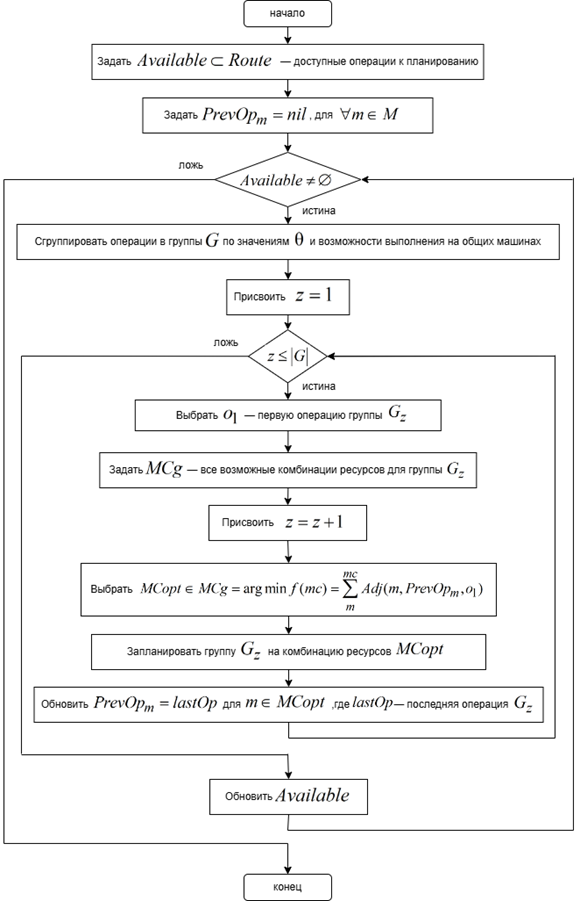
Рис. 4. Блок-схема жадного алгоритма планирования с группировкой операций
Fig. 4. Block diagram of a greedy scheduling algorithm with grouping of operations
Для каждой операции 
задан θo, набор значений свойств операции. Его размер должен быть одинаковым для каждой операции. Свойства операции описывают некоторые ее характеристики, влияющие на производственные переналадки – как правило, это характеристики обрабатываемых полуфабрикатов. Размерность вектора задается в зависимости от количества таких свойств на производстве. Если векторы одинаковы для двух операций, то предполагается, что переналадка между ними будет отсутствовать. Группировка однотипных операций является зачастую единственным способом минимизации переналадок.
Расстановка на ресурсы происходит с учетом ограничений заказа на минимальную дату старта si, времени установки предыдущей операции 
, а также времени доступности 
, операции при этом являются непрерывными.
Описание полученных результатов
С целью проверки результатов был реализован описанный в работе жадный алгоритм планирования. Исходный код написан на языке программирования C# 10 с использованием свободной платформы .NET 6.0. Было произведено несколько запусков алгоритма с различными наборами входных данных. Глубина маршрута X = 5, количество параметров θ = 9, количество машин m = 250.
Результаты тестовых запусков приведены в таблице.
Результаты тестовых запусков алгоритма
Results of test runs of the algorithm
|
№ теста |
Количество операций |
Количество |
Общее количество |
Количество операций |
Длительность |
Суммарное время |
Суммарное время |
|
1 |
2 323 |
3 569 |
881 |
5 688 |
10 |
57,08 |
183,18 |
|
2 |
9 217 |
13 050 |
3 345 |
22 280 |
102 |
178,12 |
701,69 |
|
3 |
1 786 |
2 483 |
591 |
4 116 |
5 |
46,4 |
406,62 |
|
4 |
6 069 |
7 565 |
1 970 |
13 374 |
37 |
122,1 |
858,83 |
Для апробации алгоритма были привлечены специалисты по планированию одного из российских предприятий кабельной промышленности, а также специалисты в области разработки систем планирования для других производств. По итогам тестовой эксплуатации алгоритма были получены следующие результаты:
– общий процент времени производственных переналадок составляет не более 25 % от всего времени работы машин (при ручном планировании этот показатель был выше – до 40 %);
– увеличилась скорость расчета – ручное построение расписания на сутки занимало не менее часа, разработанный алгоритм строит графики за несколько минут.
По результатам апробации разработанный алгоритм был признан эффективным для решения задач производственного планирования с минимизацией переналадок.
Заключение
Разработан и описан алгоритм оперативного планирования, учитывающий альтернативные цепочки выполнения операций в технологических процессах, экспертным путем была доказана его эффективность. Дальнейшие улучшения алгоритма – это использование более сложных и эффективных методов для расчета маршрута и его дальнейшего планирования, в частности использование эволюционных алгоритмов, а также применение генетического программирования для создания эвристик планирования без привязки к конкретной предметной области. Кроме того, необходимо исследовать
возможность объединения этапа поиска маршрута с его детальным планированием.
1. Obukhov K. O. Sravnitel'nyi analiz sistem proizvod-stvennogo planirovaniia v razreze raboty s al'ternativnymi tsepochkami proizvodstvennykh operatsii [Comparative analysis of production planning systems in the context of work with alternative chains of production operations]. Molodoi uchenyi, 2022, no. 20 (415), pp. 143-147. Available at: https://moluch.ru/archive/415/91773/ (accessed: 22.01.2024).
2. Lazarev A. A., Gafarov E. R. Teoriia raspisanii. Zadachi i algoritmy [The theory of schedules. Tasks and algorithms]. Moscow, 2011. 222 p.
3. Applegate D., Cook W. J. A Computational Study of the Job-Shop Scheduling Problem. Available at: https:// www.researchgate.net/publication/220668856_A_Computational_Study_of_the_Job-Shop_Scheduling_Problem (accessed: 22.01.2024).
4. Fangfang Zhang, Yi Mei, Su Nguyen, Mengjie Zhang. Survey on Genetic Programming and Machine Learning Techniques for Heuristic Design in Job Shop Scheduling. Available at: https://www.researchgate.net/publication/369157477_Survey_on_Genetic_Programming_and_Machine_Learning_Techniques_for_Heuristic_Design_in_Job_Shop_Scheduling (accessed: 22.01.2024).
5. Barakat L. A., Kviatkovskaia I. Iu. Planirovanie be-zopasnykh marshrutov bezekipazhnykh sudov na osnove metodov iskusstvennogo intellekta [Planning safe routes for un-manned vessels based on artificial intelligence methods]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta. Seriia: Upravlenie, vychislitel'naia tekhnika i informatika, 2023, no. 3, pp. 46-54.
6. Luk'ianov L. A., Spivak S. I., Khristoliubov V. L. Neironnaia set' korrektor dlia raspredeleniia rabot v zadache vnutritsekhovogo planirovaniia [Neural network corrector for the distribution of work in the tasks of in-house planning]. Vestnik Bashkirskogo universiteta, 2016, no. 4. Available at: https://cyberleninka.ru/article/n/neyronnaya-set-korrektor-dlya-raspredeleniya-rabot-v-zadache-vnutritsehovogo-planirovaniya (accessed: 16.02.2024).
7. Pankaj Sharma, Ajai Jain. A review on job shop scheduling with setup times. Available at: https://www.researchgate.net/publication/275317984_A_review_on_job_shop_scheduling_with_setup_times (accessed: 22.01.2024).
8. Planirovanie i optimizatsiia protsessov perenaladki [Planning and optimization of changeover processes]. Available at: https://habr.com/ru/companies/ds/articles/533788/ (accessed: 22.01.2024).
