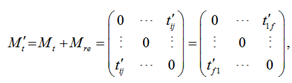Введение

Классическая теория транспортных процессов включает понятный математический аппарат, описывающий движение транспортных средств, наблюдаемые и вычисляемые параметры транспортной системы. Наблюдаемые параметры – это количество судов и их транспортных переходов, вычисляемые параметры – это скорость движения, время перехода и их различные производные. Такой подход является недостаточным для подробного изучения водно-транспортных систем организации перевозок, поскольку не учитывает внутренние связи и взаимодействие судов. Расширенное описание включает набор матриц расстояний, скоростей и времени [1–3], т. е. используется более сложный матричный аппарат, который позволяет детерминировать внутренние процессы взаимодействия судна как с водным путем, так и с другими судами. Это делает возможным за счет использования изменяемых величин (например, скорость, время стоянки) численно моделировать выполнение рейса в целом и плавание по отдельным участкам внутренних водных путей.

В стандартной практике размеры эксплуатируемого судна определяются по наименьшим габаритным значениям водного пути, т. е. по его радиусу (длине) и ширине на маршруте [4]. В то же время соотношение длины и ширины на лимитирующих участках может существенно различаться, создавая потенциальные варианты, при которых судно не проходит участок только по одному из линейных параметров и имеет запас для прохождения участка пути по второму параметру (например, проходит по ширине, но не проходит по длине) [5]. В данной работе на основе проведенных исследований [6] предлагается отказаться от линеарного подхода, заложенного в работу барже-буксирных составов (ББС) и заключающегося в прохождении составом маршрута в одной установленной конфигурации. Достичь более полного соответствия габаритов судна характеристикам внутренних водных путей и, соответственно, увеличения объема перевозок возможно за счет использования конструктивных особенностей ББС (состоят из отдельных барж) и обеспечения их перегруппировки в процессе осуществления рейса непосредственно перед стесненным участком пути для его прохождения. Подробнее технология перегруппировки составов судов на маршруте рассмотрена в [6, 7].

Изменение конфигурации состава судов для прохождения ограничивающих участков водного пути в процессе совершения рейса позволяет увеличить объем перевозимого за один рейс груза, однако при этом возрастает время рейса, создавая неопределенность касательно целесообразности ее выполнения. Решение должно приниматься, в том числе, на основе анализа скоростных и временных характеристик движения ББС с учетом перегруппировки и без нее.

Перегруппировка ББС на маршруте следования не учитывается в классическом подходе при моделировании и оценке эффективности организации перевозок грузов и требует проработки вопроса ее встраивания в общую систему расчетов численных значений параметров движения выполняемого рейса с применением матричных методов. Это определяет задачу адаптации математического аппарата транспортной системы внутренних водных путей к подходу, при котором обеспечивается более гибкая связь локальных характеристик внутренних водных путей и габаритов судов. В предыдущих исследованиях [8] для определения влияния поворотных участков водного пути на изменение времени рейса и скорости движения переменного по конфигурации ББС по маршруту следования предложена система матриц, где в качестве интегрального результата выступают уточненная матрица времени и уточненная матрица скоростей. В рамках данной работы они раскрываются более подробно.

Основной целью статьи является создание метода оценки вариантов организации перевозок грузов (сравнение и выбор наиболее эффективного). Его реализация представлена в двух частных задачах: детерминированное применение матричных методов для описания движения ББС с перегруппировкой на маршруте следования и составление расчетной модели определения эффективности и сравнения вариантов перевозок грузов ББС. Связанное решение обеих задач позволяет сформировать указанный метод и, соответственно, достичь поставленной цели исследования.

Методы и материалы исследования

В статье рассматриваются уточненная матрица времени и уточненная матрица скоростей как результирующие инструменты для оценки влияния перегруппировки состава на маршруте следования, необходимость которой возникает для прохождения стесненных участков водного пути с сохранением общего числа буксиров и барж, на среднюю скорость движения состава и общее время рейса. Основу построения матриц составляют поворотные точки водного пути, под которыми понимаются места осуществления ББС маневровых операций, и трехуровневая модель, характеризующая их типы в зависимости от степени влияния на скорость и конфигурацию ББС. Другим определяющим понятием является матрица перегруппировки, предложенная в предыдущих исследованиях [8], которая учитывает время, необходимое на изменение конфигурации состава судов на маршруте следования. Она характеризует время перестановки барж и буксиров в составе по линиям и рядам, выполняемой на определенных участках внутренних водных путей для их прохождения. Структурированный вид матрицы позволяет наглядно показать число и взаимное расположение мест переформирования состава судов.

Предлагается интегрировать матрицу перегруппировки в классическую матрицу времени путем ее пересчета, а далее произвести пересчет матрицы скоростей. Тогда интегральные матрицы строятся на основе базовой матрицы расстояний, расчетной матрицы времени (базовая матрица скоростей используется для построения расчетной матрицы времени) и матрицы перегруппировки, формирующейся с учетом анализа маршрута и грузовой базы, параметров буксиров и барж, характеристик используемых сцепных устройств.

Уточненная матрица времени (M_tʹ) представляет собой матрицу времени, откорректированную с учетом дополнительного времени, требующегося на перегруппировку ББС, тогда она выглядит следующим образом:

где M_t – расчетная матрица времени; M_re – матрица перегруппировки; tʹ_ij  – элементы уточненной матрицы времени (время, необходимое составу на прохождение участка водного пути между двумя поворотными точками, учитывающее перегруппировку состава); i, j – порядковый номер строки и столбца матрицы, которые представляются в виде порядкового номера поворотной точки на маршруте следования (f).

Уточненная матрица скоростей (M_vʹ) формируется путем деления матрицы расстояний на уточненную матрицу времени. Она показывает влияние остановок, необходимых для переформирования состава, на среднюю скорость его движения по маршруту:

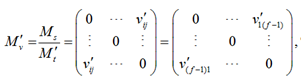
где M_s – базовая матрица расстояний; vʹ_ij – элементы уточненной матрицы скоростей (расчетная скорость на прямолинейных участках водного пути с учетом перегруппировки состава).

Уточненную матрицу скоростей можно также представить в виде матрицы-столбца, что удобно при сопоставлении с базовой матрицей скоростей:

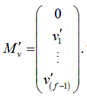
В качестве примера построения интегральных матриц выполнен расчет параметров движения ББС на участке маршрута от Нижне-Свирского шлюза до Ладожского озера. Формирование последовательности поворотных точек произведено с использованием метода аппроксимации. Из совокупности координат, полученных посредством данных автоматической идентификационной системы (АИС), выбраны точки, подпадающие под условия: ROT (скорость поворота) ≠ [–3; +3] или COG (курс относительно грунта) – Heading (гирокомпасный курс) ≠ [–5; +5]. Фрагмент аппроксимации координатных точек маршрута приведен на рис. 1. Всего было отобрано 228 поворотных точек.

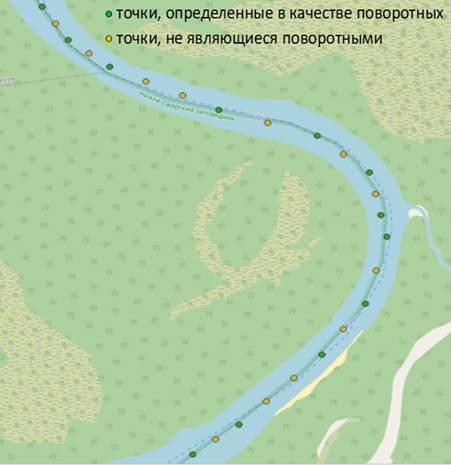
Рис. 1. Пример аппроксимации координатных точек участка водного пути
от Нижне-Свирского шлюза до Ладожского озера

Fig. 1. An example of approximation of the coordinate points of the route
from the Nizhne-Svirsky shipping lock to Lake Ladoga

Далее поворотные точки были разделены на уровни в соответствии с ранее предложенной трехуровневой моделью. Так, участок, где осуществляется маневрирование, относится к 1 уровню, если при движении по нему состав изменяет свою скорость. Поворотные участки, для прохождения по которым требуется изменение расположения барж в составе, определяются ко 2 уровню. Если дополнительно необходимо изменение положения буксиров, назначается 3 уровень. Участки, не предполагающие изменения скорости и конфигурации состава, представляют собой метауровень. Пример дискретизации участка внутреннего водного пути приведен на рис. 2. Для дифференциации поворотных точек по описанным уровням использовались данные о скорости судов-аналогов по АИС и соотношения из [6, 7].

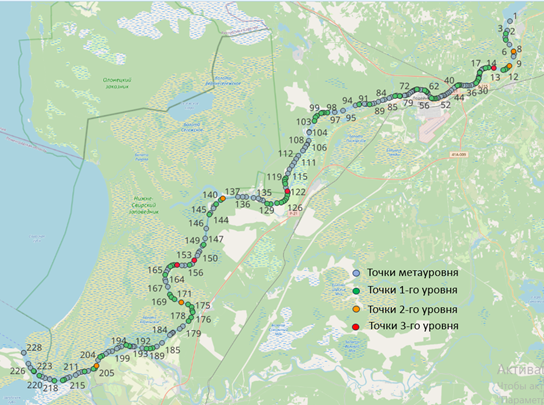
Рис. 2. Пример дискретизации участка внутреннего водного пути согласно трехуровневой модели

Fig. 2. An example of discretization of an inland waterway section according to a three-level model

Исходя из поставленной задачи, необходимо более подробно раскрыть инструмент определения эффективности рейса, на основе которого будет производиться сравнение работы ББС с перегруппировкой на маршруте следования и без нее. Таким инструментом выступает целевая функция, параметры которой – это удельный объем перевезенного груза (Q_n) и общее время рейса судна / состава судов (T_n). Выбор соответствующих параметров объясняется их основополагающим значением для организации перевозок и грузоотправителей. Это также исходит из противоречия, что при осуществлении перегруппировки составом за счет сохранения исходного числа барж перевозится больший объем груза за один рейс, чем в случае уменьшения числа барж и, соответственно, вместимости состава, однако при изменении конфигурации в пути следования увеличивается время рейса. Целевая функция представляется следующим образом:

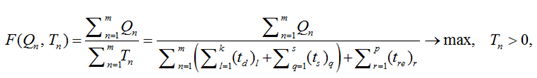                                                  (1)

где m – число выполненных рейсов; k – число участков водного пути; s – число остановок на маршруте следования, не связанных с перегруппировкой состава судов; p – число остановок на перегруппировку состава на маршруте следования; (t_d)_l – время движения судна / состава судов на каждом из участков водного пути; (t_s)_q – время остановок на маршруте следования, не связанных с перегруппировкой состава судов; (t_re)_r – время, затраченное на перегруппировку состава на маршруте следования.

Кроме того, должны выполняться ограничения, выраженные следующими условиями:

Q_n ≤ Gl_n,

где Gl_n – грузоподъемность судна / состава судов;

Q_n ≤ Gc_n,

где Gc_n – грузовместимость судна / состава судов;

ƩQ_n ≤ Gl_nN,

где N – число рейсов, выполненных для перевозки заданного объема груза;

ƩQ_n ≤ Gc_nN;

D_n > d_n(Q_n),

где D_n – глубина участка водного пути; d_n – осадка судна / состава судов.

Для варианта прохождения составом маршрута с перегруппировкой в качестве параметра «общее время рейса судна / состава судов» при расчете численного показателя целевой функции берется значение элемента уточненной матрицы времени, характеризующее время, необходимое составу на прохождение участка водного пути между двумя точками маршрута – начальной и конечной, учитывающее перегруппировку состава в пути следования.

Ниже представлена запись расчета значения целевой функции раздельно для варианта с перегруппировкой ББС и без нее. Состав параметров функций характеризует различия в способах организации перевозок.

В соответствии с формулой (1) представим время, которое затрачивается на рейс при классической организации его работы, и время рейса с переформированием на маршруте следования так, как записано в формулах:

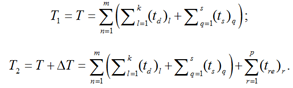
Тогда целевую функцию можно выразить следующим образом.

В классическом варианте (без перегруппировки судна / состава судов):

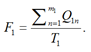
В варианте с перегруппировкой ББС:

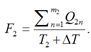
Далее сравним результат перевозки груза в двух вариантах:

– классический с неизменяемой конфигурацией ББС;

– с перегруппировкой ББС.

Результат их сравнения будет показывать, какой из методов перемещения груза эффективнее. При этом обязательным условием является сопоставление объема груза, времени перевозки (сравниваемый период) или количества рейсов, т. е. их уравнивание для сравнения (таблица). 

Параметры уравнивания целевой функции определения эффективности перевозки грузов

Parameters of equalization of the target function for determining the efficiency of cargo transportation

Параметр	Условие уравнивания	Пояснение
Объем		Спектр применения определяется необходимостью перевозки заранее известного ограниченного объема груза
Время	T1 = T2 + ΔT	Может использоваться при организации регулярных перевозок с неограниченным объемом груза в течение обозначенного периода
Число рейсов	m1 = m2	Рассматривается в случае отправки определенного числа рейсов, где и объем перевезенного груза, и время перевозки не являются регулирующими параметрами

Выбор наиболее эффективного варианта перевозок может производиться на основе применения комбинированного подхода, где в процессе моделирования работы судов учитываются или последовательно задаются несколько параметров.

Результаты исследования

Матрицы, представленные в работе, позволяют комплексно выполнить расчет временных и скоростных характеристик движения ББС по маршруту с переформированием в пути следования и решают задачу визуального представления расположения и влияния путевых точек и трехуровневой модели на время и скорость прохождения составом маршрута в целом и его отдельных участков. Интегральным результатом выступают сформированные уточненные матрицы времени и скоростей, откорректированные с учетом перегруппировки состава. Они характеризуют время и динамику прохождения составом маршрута при условии изменения его конфигурации в процессе выполнения рейса. Так, показать влияние изменения скорости судна (состава судов) и остановок в пути следования, в том числе вследствие изгибов водного пути, на время движения можно с помощью уточненной матрицы времени. Она дает возможность определить время, за которое судно проходит отдельный поворотный участок водного пути и маршрут в целом.

Уточненная матрица скоростей выступает дополнительной, характеризуя динамику прохождения маршрута, что позволяет выполнить оценку влияния на время рейса остановок, связанных с изменением конфигурации состава.

Уточненная матрица времени строится на основе расчетной матрицы времени, которая получена из базовых матриц расстояний и скоростей, и матрицы перегруппировки. Отдельно обозначаются точки, соответствующие трехуровневой модели, а также участки, на время прохождения которых оказало влияние выполнение переформирования состава на маршруте следования. При построении использовались программные средства Microsoft Excel, фрагмент приведен на рис. 3. Данная матрица становится базой для анализа эффективности рейса по времени, позволяя в сравнении делать предварительные выводы о целесообразности выполнения перегруппировки состава на маршруте следования. Так, может быть задано ограничение рейса по времени, при превышении которого вариант осуществления рейса с перегруппировкой состава на маршруте далее не рассматривается.

Уточненная матрица скоростей представляет собой базовую матрицу скоростей, откорректированную с учетом выполнения перегруппировки состава на маршруте. Скорость в процессе изменения конфигурации состава принимается равной нулю и учитывается при определении скорости прохождения участка, следующего за переформированием. Фрагмент уточненной матрицы скоростей приведен на рис. 4. При построении матрицы подробно обозначаются участки пути, где происходит изменение скорости состава: как вследствие особенностей, связанных с обеспечением безопасности движения, так и по причине переформирования состава. Детальное рассмотрение уточненной матрицы скорости позволяет провести анализ степени влияния изменения конфигурации (количества раз, продолжительности) на среднюю скорость прохождения составом маршрута.

В рамках статьи не приводится построения базовых матриц расстояний, скоростей, расчетной матрицы времени и матрицы перегруппировки, однако они вместе с уточненными матрицами времени и скоростей составляют единый комплекс, который дает возможность численно моделировать параметры движения состава с изменением конфигурации во время выполнения рейса. Таким образом, классический матричный аппарат дополняется инструментами для учета выполнения перегруппировки на маршруте.

Уточненные матрицы времени и скоростей включаются в общую систему определения эффективности потенциальных рейсов. Сравнение эффективности вариантов организации работы самоходных судов и ББС с перегруппировкой на маршруте или без нее в заданных условиях выполняется на основе сопоставления отношений перевезенного груза ко времени перевозки, которое выражено в максимизации целевой функции.

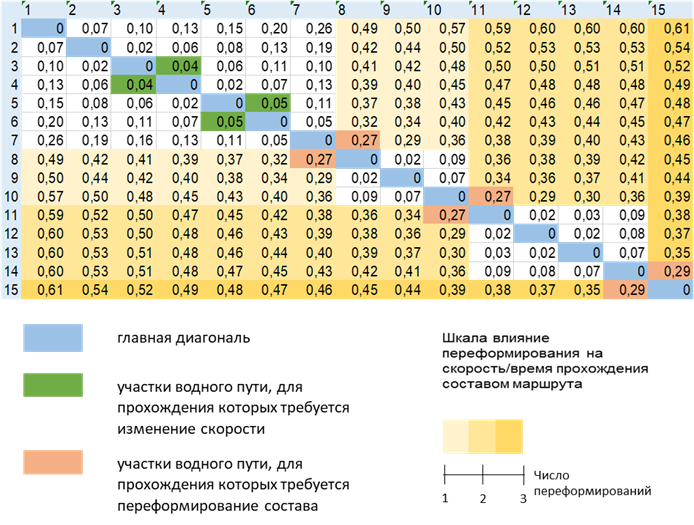
Рис. 3. Пример фрагмента уточненной матрицы времени, ч

Fig. 3. An example of a fragment of a refined time matrix, h

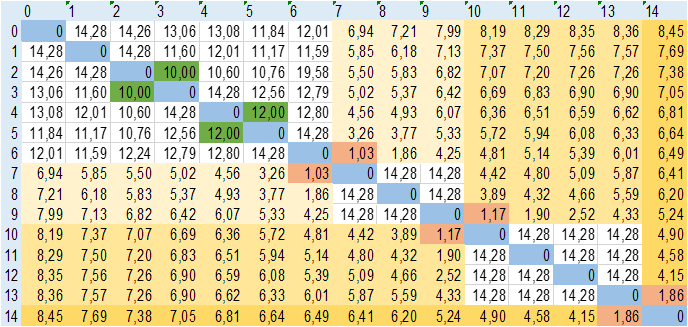
Рис. 4. Пример фрагмента уточненной матрицы скорости, км/ч

Fig. 4. An example of a fragment of the refined speed matrix, km/h

Выбор наиболее эффективного способа организации перевозок предложено осуществлять путем построения и расчета значения целевой функции. При этом параметр времени рейса соотносится с матрицей времени или уточненной матрицей времени в зависимости от потребности учета изменения конфигурации. Так, с помощью интегральных матриц процесс перегруппировки встраивается в систему расчетов показателей эффективности перемещения груза на маршруте. Параметр объема перевозок дискретно задается по каждому отдельному рейсу, при рассмотрении группы рейсов – записывается с накоплением.

На рис. 5, 6 приведена динамика изменения объемных и временных показателей в процессе выполнения рейсов. Представлены ситуации, характеризующие различные базовые данные по объему перевозимого груза. В первом случае объем груза ограничен определенным значением, при этом он должен быть полностью доставлен из одного пункта в другой. Во втором случае объем груза не ограничивается, отгрузка происходит регулярно и непрерывно в максимально возможном количестве.

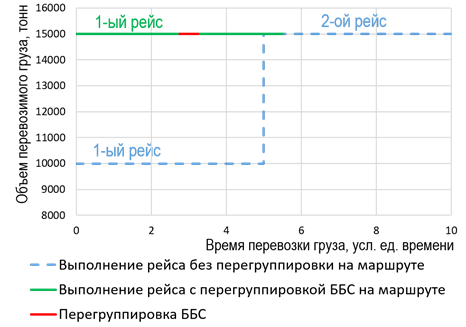
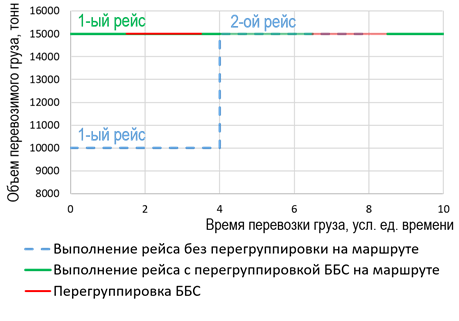
                                   а                                                                                                         б

Рис. 5. Возможные схемы перевозки при ограниченном объеме груза:
а – вариант, при котором выполнение перегруппировки на маршруте эффективней, чем выполнение рейса
без перегруппировки; б – вариант, при котором перевозка груза без перегруппировки эффективней,
чем с перегруппировкой

Fig. 5. Possible transportation schemes with a limited volume of cargo:
a – an option in which performing regrouping on the route is more effective than completing a flight without regrouping;
б – an option in which transporting cargo without regrouping is more effective than with regrouping

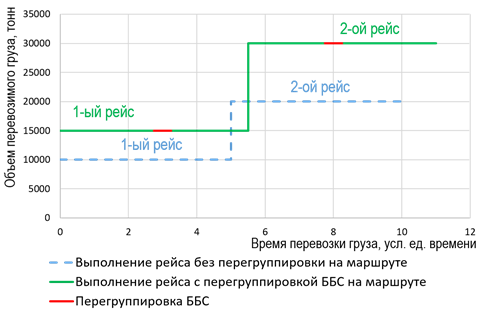
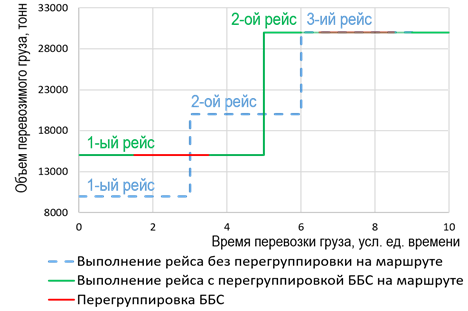
                                   а                                                                                                         б

Рис. 6. Возможные схемы перевозки без ограничений по грузу:
а – вариант, при котором выполнение перегруппировки на маршруте эффективней, чем выполнение рейса
без перегруппировки; б – вариант, при котором перевозка груза без перегруппировки эффективней,
чем с перегруппировкой

Fig. 6. Possible schemes of transportation without restrictions on cargo:
a – an option in which performing an overload on the route is more effective than performing a flight without regrouping;
б – an option in which transporting cargo without regrouping is more effective than with regrouping

Перегруппировка позволяет отказаться от дополнительных рейсов. Однако в случае наличия большого числа мест переформирования или необходимости длительных остановок, связанных с изменением конфигурации состава, преимущество по времени нивелируется. Тем не менее определение более оптимального варианта может быть неочевидным, а также зависеть от среза по значениям времени или объема. Рассматривать эффективность организации перевозок на маршруте по соотношению – объем перевозок ко времени рейса – возможно более чем для двух вариантов работы судов / составов судов. В процессе анализа уточненных матриц времени и скоростей может быть произведен отказ от переформирования на ряде участков с последующим снижением грузоподъемности состава в пользу уменьшения времени рейса. Время на изменение конфигурации может быть откорректировано за счет изменения вида сцепного устройства или сокращения числа мест переформирования на маршруте, что формирует варианты способов организации рейсов. Провести сравнительный расчет эффективности позволяет предложенная целевая функция, показывающая, какое соотношение перевезенного объема ко времени рейса будет лучше. На рис. 7–9 приведены принципиальные схемы графика целевых функций рейсов с перегруппировкой и без перегруппировки по различным параметрам. Целевая функция представляет собой рациональную функцию, расположение в положительной области построения обусловлено областью допустимых значений (все параметры функции должны быть положительны). По оси абсцисс отражается время в пути следования, по оси ординат – расчетное значение целевой функции, значение объема является известной величиной, дискретно увеличивающейся после завершения каждого отдельного рейса.

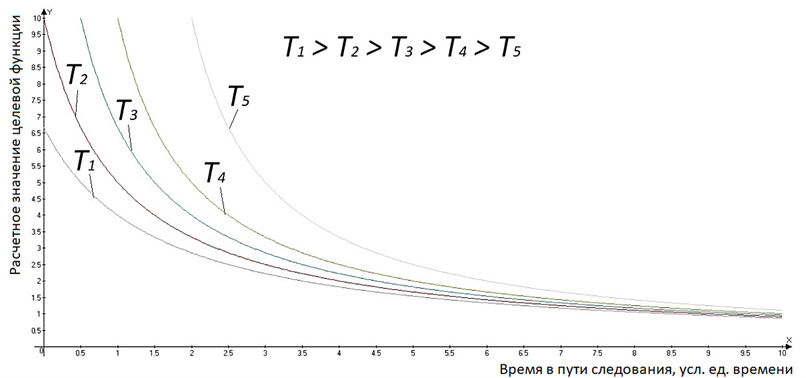
Рис. 7. Принципиальная схема построения графика целевых функций
с уравниванием по параметру объема (Q₁ = Q₂ = Q₃ = Q₄ = Q₅)

Fig. 7. Schematic diagram of the graph of objective functions with volume parameter
equalization (Q₁ = Q₂ = Q₃ = Q₄ = Q₅)

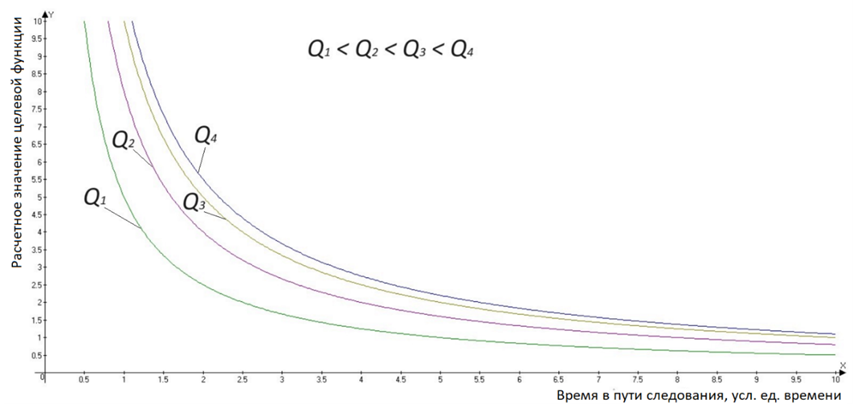
Рис. 8. Принципиальная схема построения графика целевых функций
с уравниванием по параметру времени (T₁ = T₂ = T₃ = T₄)

Fig. 8. Schematic diagram of the graph of objective functions with time parameter equalization (T₁ = T₂ = T₃ = T₄)

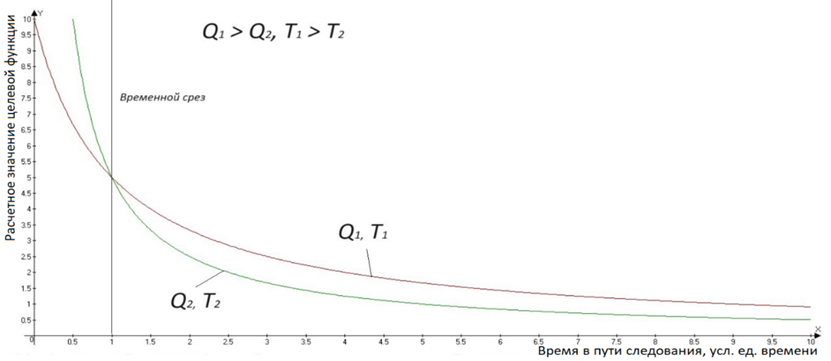
Рис. 9. Принципиальная схема построения графика целевых функций
с уравниванием по параметру количества рейсов (m₁ = m₂)

Fig. 9. Schematic diagram of the construction of a graph of objective functions with equalization
by the parameter of the number of flights (m₁ = m₂)

Построенные графики представляют собой семейство кривых. При этом расположение правее оси ординат определяет большее значение функции и более высокую эффективность реализации соответствующего способа организации перевозок по сравнению с сопоставляемыми. На рис. 9 наглядно представлена ситуация, при которой сравнительная эффективность двух вариантов изменяется по времени рейса, а точка пересечения характеризует момент, когда значение одной целевой функции превысило значение другой (сначала преимущество имеет второй вариант организации перевозок, после пересечения – первый вариант).

Вычисление значения целевой функции позволяет количественно сравнить эффективность организации перевозки по соотношению объема перевезенного груза и времени рейса / группы рейсов. На рис. 10 приведен пример вариантного сравнения эффективности возможной работы судов на маршруте при условии заданного объема перевозки. В кружках на рисунке обозначены значения целевой функции. В данном случае более эффективным является 1-й вариант рейса с перегруппировкой.

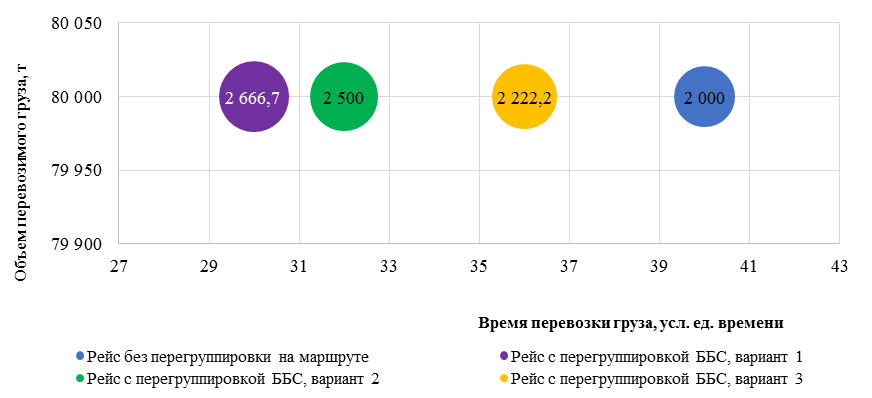
Рис. 10. Соотношение эффективности способов организации перевозки груза
по расчетному значению показателя целевой функции

Fig. 10. The ratio of the effectiveness of the methods of organizing cargo transportation according
to the calculated value of the indicator of the target function

Таким образом, метод определения эффективности организации перевозок грузов ББС, в том числе с перегруппировкой на маршруте следования, можно представить комплексом инструментов и действий, которые заключаются в расчете параметров движения в матричном виде, построении графиков целевой функции, вычислении ее расчетных значений и их сравнении между собой, анализе и подборе значений, наиболее удовлетворяющих критерию максимизации целевой функции.

Обсуждение

Использование матричных методов для моделирования работы транспортной сети имеет положительный опыт для автомобильного, железнодорожного и морского транспорта [9–11]. Подобные исследования на внутреннем водном транспорте менее распространены, но в последнее время получили новое развитие. Так, в статьях [12, 13] с применением матричного аппарата рассматриваются перевозки грузов на реке Янцзы, в работе [14] матрицы используются при изучении вопроса задержек шлюзования в верховьях реки Миссисипи. В рамках данного исследования система матриц приводится в качестве основы для анализа различных вариантов организации рейсов, в том числе с перегруппировкой ББС на маршруте, и базы для сравнения их эффективности.

Решающими факторами при выборе варианта грузоперевозки являются ее время и стоимость. В отношении внутреннего водного транспорта в качестве преимущества обозначается низкая себестоимость перевозок [15, 16]. По времени выполнения рейсов (скорости доставки грузов) перевозки по воде уступают наземным видам транспорта, что по совокупности рейсов может быть компенсировано большим объемом перевозок за одно отправление. Подробней рассмотреть эффективность организации работы судов на маршруте позволяют приведенные в статье расчетные уточненные матрицы и целевая функция. Система расчетных матриц позволяет подробно проанализировать временные и скоростные параметры движения судов на маршруте и принять возможные меры по их оптимизации. Целевая функция показывает эффективность выполнения рейса с позиции перемещения определенного объема груза за обозначенное время. Сравнение полученных значений целевой функции на основе критерия максимизации результата приводит к выбору наиболее эффективного варианта организации перевозок (при этом экономический эффект требует дополнительного детального уточнения). Расчет может производиться с установленными ограничениями по количеству перевозимого груза, рейсов или времени перевозки. Параметр времени особенно важен. Он может иметь определяющее значение для ряда грузовладельцев и для отдельных видов груза. Для случая превышения расчетного времени рейса по установленному ограничению такой вариант исключается из рассмотрения. В рамках данной статьи не рассматривались промежутки ожиданий между рейсами, влияние гидрометеоусловий на скорость движения ББС, эти факторы будут проанализированы и учтены в дальнейших исследованиях.

Заключение

Приведенные интегральные матрицы времени и скоростей позволяют учесть и отдельно выделить процесс изменения конфигурации состава судов при выполнении рейса. Визуальное представление параметров движения по участкам водного пути становится базой для варьирования составляющими работы ББС за счет включения и исключения его отдельных перегруппировок на маршруте следования. Сравнение эффективности различных возможных способов организации перевозок предлагается производить на основе расчета значения целевой функции, построения ее графиков, а также графиков соотношений объемов перевозимого груза ко времени рейса / группы рейсов. Совокупность предлагаемых инструментов и последовательность их применения позволила сформировать метод определения эффективности вариантов организации перевозок ББС с перегруппировкой и без перегруппировки составов барж на маршруте следования. Таким образом, в процессе достижения цели и поставленных задач исследования получены следующие научные результаты:

1. Сформированы математические основы учета перегруппировки состава на маршруте следования – представляют собой интегральные матрицы времени и скоростей, которые становятся частью классических матриц движения судов.
2. Разработана целевая функция, на основе которой определяется эффективность выполнения перевозок грузов, в том числе сравнение вариантов организации перевозок с перегруппировкой на маршруте следования и без нее. Предложен общий вид целевой функции и отдельно по основным способам организации рейсов.
3. Определены параметры уравнивания и ограничения целевой функции.
4. Приведены графики, построение которых демонстрирует различия между способами организации рейсов.

1. Li H., Liu J., Liu R. W., Xiong N., Wu K., Kim T. A dimensionality reduction-based multi-step clustering method for robust vessel trajectory analysis. Sensors, 2017, vol. 17, no. 8, p. 1792.

2. Butsanets A., Ol'khovik E., Karetnikov V., Senchenko V. Issues of building an intelligent water transport management system. E3S Web of Conferences. EDP Sciences, 2021. Vol. 326. P. 00029.

3. Sakharov V. V., Chertkov A. A., Ochina L. B. Marshrutizatsiia setei s otritsatel'nymi vesami zven'ev v pakete optimizatsii MATLAB [Routing of networks with negative link weights in the MATLAB optimization package]. Vestnik Gosudarstvennogo universiteta morskogo i rechnogo flota imeni admirala S. O. Makarova, 2019, vol. 11, no. 2, pp. 230-242.

4. Egorov G. V. Vybor osnovnykh parametrov korpusov sudov smeshannogo plavaniia dlia «severnogo zavoza» [Selection of the main parameters of the hulls of mixed navigation vessels for the “northern delivery”]. Trudy Tsentral'nogo nauchno-issledovatel'skogo instituta imeni akademika A. N. Krylova, 2010, no. 55, pp. 47-56.

5. Zhidkova A. M., Ol'khovik E. O. Sravnitel'nyi analiz sootnoshenii kharakteristik vnutrennikh vodnykh putei i gabaritnykh parametrov barzhe-buksirnykh sostavov [Comparative analysis of the ratios of the characteristics of inland waterways and the overall parameters of barge-tow trains]. Transportnoe delo Rossii, 2023, no. 5, pp. 232-237.

6. Zhidkova A. M. Optimizatsiia konfiguratsii barzhe-buksirnykh sostavov v zavisimosti ot gabaritnykh i navigatsionnykh kharakteristik vnutrennikh vodnykh putei [Optimization of the configuration of barge-tow trains depending on the overall and navigational characteristics of inland waterways]. Vestnik Gosudarstvennogo universiteta morskogo i rechnogo flota imeni admirala S. O. Makarova, 2022, vol. 14, no. 5, pp. 722-735. DOI:https://doi.org/10.21821/2309-5180-2022-14-5-722-735.

7. Zhidkova A. M., Ol'khovik E. O. Sposob formirovaniia sudovogo sostava [The method of formation of the ship's composition]. Patent RF, no. 2022121005; 19.12.2022.

8. Zhidkova A. M. Modelirovanie raboty barzhe-buksirnykh sostavov metodom mat-richnoi marshrutizatsii [Modeling the operation of barge-tow trains using the matrix routing method]. Vestnik gosudarstvennogo universiteta morskogo i rechnogo flota imeni admirala S. O. Makarova, 2023, vol. 15, no. 6, pp. 1015-1029. https://doi.org/10.21821/2309-5180-2023-15-6-1015-1029.

9. Domke E. R., Zhestkova S. A., Barsukova A. I. Optimizatsiia sistemy dostavki massovogo stroitel'nogo gruza avtomobil'nym transportom [Optimization of the system of delivery of mass construction cargo by road]. Regional'naia arkhitektura i stroitel'stvo, 2020, no. 3, pp. 152-160.

10. Kuznetsov V. G., Kozlov V. G., Kozlov M. G. Raschet ob"emov transportnogo potoka po napravleniiam zheleznodorozhnoi seti [Calculation of the volume of traffic flow in the directions of the railway network]. Vestnik Belorusskogo gosudarstvennogo universiteta: nauka i transport, 2011, no. 1, pp. 68-71.

11. Shramko A. P., Andreev S. V. Razrabotka prognoznykh modelei razvitiia regional'noi transportnoi sistemy [Development of forecast models for the development of the regional transport system]. Ekspluatatsiia morskogo transporta, 2017, no. 2, pp. 20-26.

12. An F., Hu H., Xie C. Service network design in inland waterway liner transportation with empty container repositioning. European Transport Research Review, 2015, vol. 7, no. 2, pp. 1-11.

13. Deng G., Zhong M., Lei M., Hunt J. D., Wang W., Zhou Y. Freight distribution analysis and modelling of in-land waterway transport using big data. Proceedings of the Institution of Civil Engineers-Transport. Thomas Telford Ltd, 2022. Pp. 1-19.

14. Yu T. E., Sharma B. P., English B. C. Investigating lock delay on the upper Mississippi river: a spatial panel analysis. Networks and Spatial Economics, 2019, vol. 19, pp. 275-291.

15. Pantina T. A., Borodulina S. A. Kriterii i faktory rosta konkurentosposobnosti vnutrennego vodnogo transporta [Criteria and factors for the growth of competitiveness of inland waterway transport]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta. Seriia: Ekonomika, 2018, no. 3, pp. 68-77.

16. Bekker R. V. Preimushchestva gruzovykh perevozok vnutrennim vodnym transportom. Menedzhment [Advantages of freight transportation by inland waterway. Management]. Materialy 54-i Mezhdunarodnoi nauchnoi studencheskoi konferentsii MNSK-2016 (Novosibirsk, 16–20 aprelia 2016 g.). Novosibirsk, Izd-vo NGU, 2016. P. 15.