Russian Federation
Russian Federation
Russian Federation
Russian Federation
Russian Federation
Optimization of the parameters of the product manufacturing process is one of the key tasks of technological preparation of production. The technological process of mechanical processing has a complex hierarchical struc-ture. The effectiveness of optimizing the manufacturing process of a product directly depends on the level of its detail and the optimal choice of targets and control parameters. In this case, the technological process of mechanical processing, as an object of control, can be described in the form of a hierarchical model. Thus, the task of optimizing the technological process of mechanical processing is to determine the optimal values of control parameters for each structural element (intermediate state of the control object) of the hierarchical control model. The aim of the work is to develop a hierarchical model for optimizing the parameters of a complex of working transitions for machining operations. The structure of the hierarchical model of the product manufacturing process on metal-cutting machines is described. Within the framework of the developed model, five control levels are identified, control parameters for individual structural elements of the model are defined, as well as the relationship between them. For the intermediate states of the control object (structural elements), a description of single and vector optimization criteria is presented. The practical implementation of the developed control model is presented using the example of optimizing the technological parameters for the “Bushing” part. The application of the developed control model will increase the efficiency of the technological process of manufacturing products on metal-cutting machines by optimizing technological parameters based on a multi-criteria analysis at the stage of technological preparation of production.
technological process, vector optimization criterion, particular optimization criterion, hierarchical model, structural elements, mechanical processing, technological transition, technological operation
Введение
Быстрые темпы развития производства и высокая конкуренция способствуют все более широкому внедрению цифровых технологий в производственный процесс. В современных экономических условиях цифровизация производственных процессов является одним из основных направлений развития промышленных предприятий [1]. Цифровые технологии позволяют значительно повысить эффективность хозяйственной деятельности предприятия за счет создания многоуровневой системы, позволяющей оптимизировать параметры производственных потоков на основе многокритериального анализа [2].
Проблеме оптимизации производственных процессов и внедрения цифровых технологий посвящено большое количество научных работ [3–12]. Современные цифровые технологии, такие как Интернет вещей, облачные вычисления, аналитика больших данных и искусственный интеллект, позволяют значительно повысить эффективность производственного процесса [13].
В основе оптимизации производственных процессов лежит аналитика большого объема данных, включающая сбор данных, их обработку и анализ на основе разработанных методов и алгоритмов [14–16].
В настоящее время для решения задач оптимизации широко применяются графы знаний [17, 18]. Граф знаний представляет собой семантическую сеть, в которой содержится информация о структурных элементах объекта исследования и связях между ними. Применение графов знаний для решения практических производственных задач рассмотрено в работах [19–21].
Также широкое распространение для решения задач оптимизации получили методы, базирующиеся на генетических алгоритмах, основанных на естественном процессе отбора, имитирующем биологическую эволюцию [18]. Примеры решения задач оптимизации, в основе которых лежит генетический алгоритм, представлены в работах [22–24].
В научной литературе также представлены примеры решения задач оптимизации, основанные на методе прямого поиска [25–28]. Данная группа методов относится к методам нулевого порядка, которые предполагают использование только значения функции и неиспользование ее производной.
Одним из ключевых показателей эффективности работы предприятия является качество выпускаемой продукции. Для оптимизации данного целевого показателя применяется метод Тагути [29–31], который позволяет оценить показатели качества производимой продукции и потери, возникающие по мере отклонения значений технического параметра изделия от номинального, в том числе и в пределах допуска.
Целью исследования является разработка модели оптимизации технологических параметров процесса механической обработки для повышения ее эффективности.
Задачами исследования являются анализ факторов, влияющих на эффективность механической обработки; разработка иерархической модели процесса обработки изделий на металлорежущих станках; формирование векторных критериев оптимизации для структурных элементов модели.
Объектом управления является процесс обработки изделия на металлорежущих станках.
Изделие как объект управления
Переход объекта управления из состояния заготовки в состояние готового изделия происходит на основе реализации технологического процесса, содержащего четкую последовательность действий, направленных на изменение структуры и свойств исходной заготовки, в результате выполнения которых получается изделие с заданными техническими параметрами, с применением специализированной оснастки и технологического оборудования. В рамках данной работы будет рассмотрен процесс изготовления изделия на металлорежущих станках.
Объект управления представляет собой описание четкой последовательности промежуточных состояний изделия в процессе его изготовления и средств, необходимых для перехода объекта управления из
(i – 1)-го состояния в (i)-е состояние.
Процесс изменения структуры и свойств изделия в процессе его изготовления можно представить в виде 5-уровневой иерархической модели, содержащей следующие уровни управления:
– уровень № 1 – технологический процесс;
– уровень № 2 – этап обработки;
– уровень № 3 – технологическая операция;
– уровень № 4 – технологический переход;
– уровень № 5 – рабочий ход.
На первом уровне объект управления имеет два состояния: Sзаг – состояние изделия до начала процесса обработки, Sизд – состояние изделия после завершения выполнения всех технологических операций (рис. 1).
Рис. 1. Граф первого уровня управления объектом «Изделие»:
Езаг–изд – условия перехода объекта управления из состояния Sзаг в состояние Sизд
Fig. 1. Graph of the first level of control of the “Product” object:
Езаг–изд – conditions of control object transition from Sзаг to Sизд state
Задачами данного уровня управления являются:
– оптимизация количества этапов обработки в рамках технологического процесса;
– оптимизация типов обработки в рамках каждого этапа.
Частными критериями оптимизации для данного уровня управления будут являться: 
– трудоемкость изготовления изделия в рамках технологического процесса, ч; 
– величина оперативных затрат в рамках технологического процесса, руб.; 
– индекс точности достижения заданных технических параметров в рамках технологического процесса; 
– величина капитальных затрат, необходимых для изготовления изделия, руб.
Таким образом, векторный критерий оптимизации будет иметь вид
,
где U – вектор параметров управления.
Параметрами управления в рамках данного уров-ня управления будут являться: Ntr – количество этапов обработки, шт.; Typetr – тип обработки в рамках этапа обработки.
На втором уровне переход объекта управления из состояния 
в состояние 
производится в рамках этапа обработки (рис. 2).
Рис. 2. Граф второго уровня управления объектом «Изделие»:
S21, S22, S2(k–1), S2k – 1–k-е промежуточные состояния объекта на втором уровне управления;
Езаг–21, Е21–22, Е2(k–1)–2k, Е2k–изд – условия изменения промежуточных состояний объекта управления Sзаг Þ S21,
S21 Þ S22, S2(k–1) Þ S2k, S2k Þ Sизд; k – количество промежуточных состояний объекта на втором уровне управления
Fig. 2. Graph of the second level of control of the “Product” object:
S21, S22, S2(k-1), S2k – 1-k-th intermediate states of the object at the second control level;
Езаг–21, Е21–22, Е2(k–1)–2k, Е2k–изд – conditions of control object transition Sзаг Þ S21,
S21 Þ S22, S2(k–1) Þ S2k, S2k Þ Sизд; k – number of intermediate object states in the second control level
Задачами второго уровня управления являются:
– оптимизация технологического маршрута в рамках этапа обработки;
– оптимизация количества технологических операций в рамках этапа обработки.
Частными критериями оптимизации для второго уровня управления будут являться: 
– трудоемкость изготовления изделия в рамках k-го этапа обработки, ч; 
– величина оперативных затрат в рамках k-го этапа обработки, руб.; 
– индекс точности достижения заданных технических параметров в рамках k-го этапа обработки; 
– величина капитальных затрат, необходимых для реализации k-го этапа обработки, руб.
Таким образом, векторный критерий оптимизации для k-го этапа обработки будет иметь вид
.
Параметрами управления в рамках данного этапа будут являться: Nop – количество технологических операций в рамках этапа обработки, шт.; Typeeq – тип применяемого оборудования в рамках этапа обработки.
На третьем уровне объект управления имеет следующие промежуточные состояния:
где k – количество этапов обработки в рамках технологического процесса, шт.; n – количество промежуточных состояний объекта управления в рамках этапа обработки, шт.
Переход объекта управления из состояния 
в состояние 
производится в рамках выполнения технологической операции (рис. 3).
Рис. 3. Граф третьего уровня управления объектом «Изделие»
Fig. 3. Graph of the third level of control of the “Product” object
Задачами третьего уровня управления являются:
– оптимизация структуры технологических операций;
– оптимизация номенклатуры технологического оборудования и установочно-зажимных приспособлений для каждой технологической операции;
– оптимизация используемых методов формообразования в рамках технологической операции.
Частными критериями оптимизации для третьего уровня управления являются: 
– трудоемкость выполнения работ в рамках n-й технологической операции, ч; 
– величина оперативных затрат в рамках n-й технологической операции, руб.; 
– индекс точности достижения заданных технических параметров в рамках n-й технологической операции.
Таким образом, векторный критерий оптимизации для n-й технологической операции будет иметь вид
.
Параметрами управления в рамках третьего этапа будут являться: Ntt – количество технологических переходов в рамках технологической операции, шт.; Typeeq-u – модель технологического оборудования, применяемого в рамках технологической операции; Typeif – модель установочно-зажимного приспособления, применяемого в рамках технологической операции; 
– методы формообразования, применяемые в рамках технологических переходов 1, ..., k.
Четвертый уровень управления в рамках технологической операции имеет следующие промежуточные состояния:
, где v – количество промежуточных состояний объекта управления в рамках технологической операции, шт.
Переход объекта управления из состояния 
в состояние 
производится в рамках выполнения технологического перехода (рис. 4).
Задачами четвертого уровня управления являются:
– оптимизация номенклатуры режущего инструмента, используемого в рамках технологического перехода;
– оптимизация схем обработки (траектории движения режущего инструмента) в рамках технологического перехода.
Частными критериями оптимизации для четвертого уровня управления являются: 
– трудоемкость выполнения работ в рамках v-го технологического перехода, ч; 
– величина оперативных затрат в рамках v-го технологического перехода, руб.; 
– индекс точности достижения заданных технических параметров в рамках v-го технологического перехода.
Таким образом, векторный критерий оптимизации для v-го технологического перехода будет иметь вид
Параметрами управления в рамках четвертого этапа будут являться: 
– модель режущего инструмента, применяемого в рамках технологического перехода; 
– схема траектории движения режущего инструмента.
На пятом уровне изменение промежуточного состояния объекта управления производится в результате выполнения рабочего хода. В рамках отдельного технологического перехода объект управления имеет следующие промежуточные состояния:
где r – количество промежуточных состояний объекта управления в рамках технологического перехода, шт. (рис. 5).
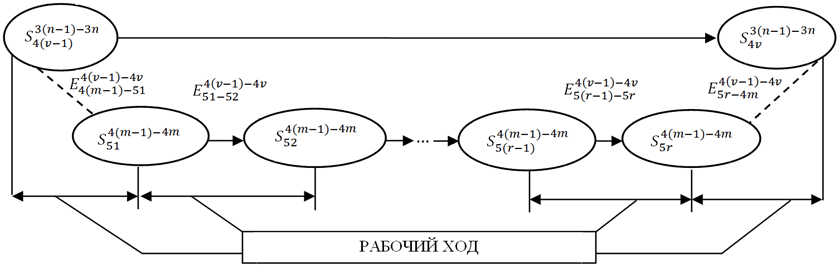
На пятом уровне управления решается задача оптимизации значений параметров резания в рамках рабочего хода.
Частными критериями оптимизации для данного уровня управления являются: 
– трудоемкость выполнения работ в рамках r-го рабочего хода, ч; 
– величина оперативных затрат в рам-
ках r-го рабочего хода, руб.; 
– индекс точности достижения заданных технических параметров в рамках r-го рабочего хода.
Таким образом, векторный критерий оптимизации для r-го рабочего хода будет иметь вид
Параметрами управления в рамках пятого уровня будут являться параметры резания, в частности S – величина подачи; V – величина скорости резания, м/мин; t – величина глубины резания, мм.
Оптимизация параметров технологического процесса изготовления детали «Втулка»
В рамках этапа технологической подготовки производства поставлена задача оптимизации параметров технологического процесса изготовления
детали «Втулка» (рис. 6).
Рис. 6. Твердотельная модель детали «Втулка»
Fig. 6. Solid-state model of the Bushing part
На рис. 7 представлена последовательность изменения состояний изделия «Втулка» в рамках первого и третьего уровней управления.
Рис. 7. Последовательность изменения состояний изделия «Втулка» в рамках первого и третьего уровней управления:
S31, S32, S33, S34 – промежуточные состояния объекта на третьем уровне управления;
Eзаг-21, E21-22, E22-23, E23-24, E24-изд – условия изменения промежуточных состояний объекта управления Sзаг Þ S31,
S31 Þ S32, S32 Þ S33, S33 Þ S34, S34 Þ Sизд
Fig. 7. The sequence of changing the states of the “Bushing” product within the first and third control levels:
S31, S32, S33, S34 – intermediate states of the object at the third management level;
Eзаг-21, E21-22, E22-23, E23-24, E24-изд – conditions of control object transition Sзаг Þ S31,
S31 Þ S32, S32 Þ S33, S33 Þ S34, S34 Þ Sизд
Изготовление изделия производится в рамках одного этапа обработки, поэтому граф измерения состояния объекта в рамках второго уровня управления идентичен графу первого уровня управления
На рис. 8 представлена последовательность промежуточных состояний изделия для четвертого и пятого уровней управления для технологической операции, в рамках которой производится переход изделия из состояния Sзаг в состояние S31.
Целями оптимизации являются:
– состояние объекта управления 
: снижение значения целевого показателя 
не менее чем на 15 %, при этом увеличение значения целевого показателя 
не должно превышать 7 %;
– состояние объекта управления
: снижение значения целевого показателя 
не менее чем на 5,5 %, при этом увеличение целевого показателя 
не должно превышать 10 %.
В рамках исходного технологического процесса (до процесса оптимизации) параметры технологического процесса имели следующие значения:
Промежуточное состояние 
59,693 с; 
.
Промежуточное состояние 
15,271 с; 
.
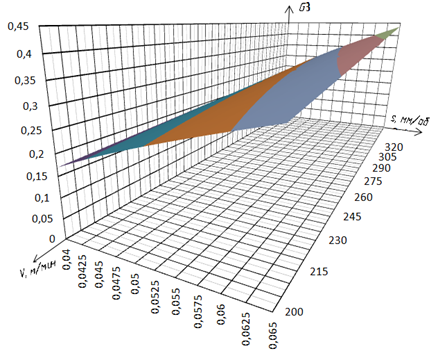
Графики зависимости значений частных критериев оптимизации от параметров управления для промежуточных состояний объекта управления 
(при фиксированной глубине резания t1 = 1,0 мм)
и 
(при фиксированной глубине резания t1 = 0,6 мм) представлены на рис. 9, 10.
а б
в
Рис. 9. Графики зависимости значений частых критериев оптимизации для промежуточного состояния объекта управления от подачи и скорости резания при глубине резания t = 1,0 мм:
а – зависимость трудоемкости выполнения рабочего хода;
б – зависимость величины затрат на выполнение рабочего хода; в – зависимость значения индекса точности
Fig. 9. Graphs of the dependence of the values of particular optimization criteria for the intermediate state of the control object on the feed and cutting speed at cutting depth t = 1.0 mm:
a – dependence of the labor intensity of the stroke;
б – dependence of the cost of the stroke; в – dependence of the accuracy index value
а б
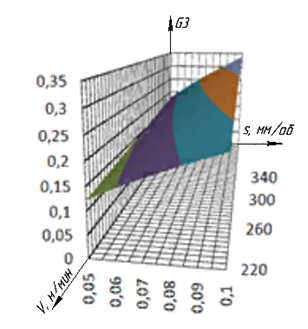
в
Рис. 10. Графики зависимости значений частых критериев оптимизации для промежуточного состояния объекта управления от подачи и скорости резания при глубине резания t = 0,6 мм:
а – зависимость трудоемкости выполнения рабочего хода;
б – зависимость величины затрат на выполнение рабочего хода; в – зависимость значения индекса точности
Fig. 10. Graphs of the dependence of the values of frequent optimization criteria for the intermediate state of the control object on the feed and cutting speed at the cutting depth t = 0.6 mm:
a – dependence of the labor intensity of the stroke;
б – dependence of the cost of the stroke; в – dependence of the accuracy index value
Параметры перехода объекта управления из состояния Sзаг в состояние 
, а также из состояния 
представлены в таблице.
Значения параметров резания
в процессе изменения состояний объекта управления 
Values of cutting parameters
in the process of changing the states of the control object 
|
Изменение состояния |
Значения параметров управления |
|||||
|
До оптимизации |
После оптимизации |
|||||
|
t |
s |
v |
t |
s |
v |
|
|
|
1,0 |
0,045 |
190 |
1,0 |
0,0525 |
220 |
|
|
0,6 |
0,075 |
310 |
0,6 |
0,07 |
305 |
В результате проведенной оптимизации промежуточные состояния имеют следующие значения целевых показателей:
Промежуточное состояние
45,316 с; 
. Снижение значения целевого показателя 
составляет 24,8 %, при этом увеличение значения целевого показателя 
– 6,44 %.
Промежуточное состояние 
= 16,649 с; 
. Снижение значения целевого показателя 
составляет 6,45 %, при этом увеличение целевого показателя 
– 9,02 %.
Заключение
Оптимизация целевых показателей технологического процесса является ключевым фактором повышения эффективности процесса изготовления изделия. Эффективность процесса оптимизации напрямую зависит от степени детализации объекта управления. Представленная в работе иерархическая модель технологического процесса механической обработки представляет собой структурную декомпозицию целей, которые должны быть достигнуты в рамках выделенных уровней управления. Данная иерархия целей позволяет повысить эффективность технологического процесса за счет детального анализа и оптимизации целевых показателей отдельных структурных элементов модели
1. Abe Zeid, Sarvesh Sundaram, Mohsen Moghaddam, Sagar Kamarthi, Tucker Marion. Interoperability in Smart Manufacturing: Research Challenges. Machines, 2019, vol. 7 (2), p. 21. https://doi.org/10.3390/machines7020021.
2. Khrustaleva I. N., Larionova T. A., Lyubomudrov S. A., Chernykh L. G., Stepanov S. N. Automating production engineering for custom and small-batch production on the basis of simulation modeling. Journal of Physics: Conference Series, 2021, vol. 1753, p. 012047.
3. Kostenko D., Shkodyrev V., Onufriev V. Solving Multicriteria Optimization Problem for an Oil Refinery Plant. Proceedings of International Scientific Conference on Telecommunications, Computing and Control, 2021, pp. 131-140.
4. Kostenko D., Arseniev D., Shkodyrev V., Onufriev V. Pareto optimization in oil refinery. Data Mining and Big Data. Communications in Computer and Information Sci-ence, 2020, pp. 26-33.
5. Kudryavtsev E. Automation of optimization of dis-crete technological processes. 27th Russian-Polish-Slovak Seminar, Theoretical Foundation of Civil Engineering (27RSP), TFOCE 2018 (Rostov-on-Don, 17–21 September 2018), MATEC Web of Conferences. 2018. Vol. 196. P. 04067. DOI:https://doi.org/10.1051/matecconf/201819604067.
6. Efimov A., Gorkavyy M., Egorova V., Gorkavyy A. Optimization of Technological Parameters of Robotized Mechanical Processing Processes of Aviation Products. Current Problems And Ways Of Industry Development: Equipment And Technologies (Warsaw, 01 January – 31 December 2021). Warsaw, Springer, 2021. Vol. 200. Pp. 204-215. DOI:https://doi.org/10.1007/978-3-030-69421-0_22.
7. Yong Xu, Ling Yuan, Khalfaoui R., Radulescu M., Mallek S., Xin Zhao. Making technological innovation greener: Does firm digital transformation work? Technological Forecasting and Social Change, 2023, vol. 197, p. 122928. https://doi.org/10.1016/j.techfore.2023.122928.
8. Martyn Ye., Liaskovska S., Gregus M., Izonin I., Velyka O. Optimization of Technological’s Processes Industry 4.0 Parameters for Details Manufacturing via Stamping: Rules of Queuing Systems. Procedia Computer Science, 2021, vol. 191, pp. 290-295. https://doi.org/10.1016/j.procs.2021.07.036.
9. Levchenko E. Machine learning as a tool for optimization of technological processes. World of petroleum products, 2021, vol. 02, pp. 44-47. DOI:https://doi.org/10.32758/2782-3040-2021-1-1-44-47.
10. El Maraghy H., Schuh G., El Maraghy W., Piller F., Schönsleben P., Tseng M., Bernard A. Product variety management. CIRP Annals, 2013, vol. 62, iss. 2, pp. 629-652. https://doi.org/10.1016/j.cirp.2013.05.007.
11. Tkach E., Semenov V., Shumilina Yu. Optimization of the composition and technological processes of dispersed cement systems with high performance properties. IOP Conference Series: Materials Science and Engineering, 2021, vol. 1030, p. 012024. DOI:https://doi.org/10.1088/1757-899X/1030/1/012024.
12. Shanin I. Methodology for the implementation of a technological solution, taking into account the optimization of production business processes based on simulation. IOP Conference Series: Materials Science and Engineering, 2021, vol. 1064 (1), p. 012037. DOI:https://doi.org/10.1088/1757-899X/1064/1/012037.
13. Tao Fei, Qi Qinglin, Wang Lihui, Nee Andrew. Digital Twins and Cyber–Physical Systems toward Smart Manufacturing and Industry 4.0: Correlation and Comparison. Engineering, 2019, vol. 5, pp. 653-661. DOI:https://doi.org/10.1016/j.eng.2019.01.014.
14. Kai Kang, Ray Y. Zhong. A methodology for pro-duction analysis based on the RFID-collected manufacturing big data. Journal of Manufacturing Systems, 2023, vol. 68 (1), pp. 628-634. https://doi.org/10.1016/j.jmsy.2023.05.014.
15. Shuaiyin Ma, Yingfeng Zhang, Jingxiang Lv, Yun-tian Ge, Haidong Yang, Lin Li. Big data driven predictive production planning for energy-intensive manufacturing industries. Energy, 2020, vol. 211, p. 118320. https://doi.org/10.1016/j.energy.2020.118320.
16. Yongheng Zhang, Rui Zhang, Yizhong Wang, Hongfei Guo, Ray Y. Zhong, Ting Qu, Zhiwu Li. Big data driven decision-making for batch-based production systems. Procedia CIRP, 2019, vol. 83, pp. 814-818. https://doi.org/10.1016/j.procir.2019.05.023.
17. Pan J., Vetere G., Manuel Gomez-Perez J., Wu H. Exploiting Linked Data and Knowledge Graphs in Large Organisations. Springer Cham, 2017. 266 p. https://doi.org/10.1007/978-3-319-45654-6.
18. Mst. Mim Akter, Md-Mizanur Rahoman. A Systematic Review on Knowledge Graphs Classification and Their Various Usages // Artificial Intelligence Evolution. 2023. P. 187–215. DOI:https://doi.org/10.37256/aie.4220233605.
19. Fensel D., Şimşek U., Angele K., Huaman E., Kärle E., Panasiuk O., Toma I., Umbrich J., Wahler A. How to Use a Knowledge Graph // Knowledge Graphs. Springer, Cham, 2020. P. 69–93. https://doi.org/10.1007/978-3-030-37439-6_3.
20. Jawad M. S., Chitra Dhawale, Azizul Azhar Bin Ramli, Hairulnizam Mahdin. Adoption of knowledge-graph best development practices for scalable and optimized manufacturing processes. MethodsX, 2023, vol. 10, p. 102124. https://doi.org/10.1016/j.mex.2023.102124.
21. Xin-She Yang. Chapter 6 - Genetic Algorithms. Nature-Inspired Optimization Algorithms. Academic Press, 2021. Pp. 91-100. https://doi.org/10.1016/B978-0-12-821986-7.00013-5.
22. Shahram Ghadami, Hassan Biglarian, Hossein Beyrami, Mohsen Salimi. Optimization of multilateral well trajectories using pattern search and genetic algorithms. Results in Engineering, 2022, vol. 16, p. 100722. https://doi.org/10.1016/j.rineng.2022.100722.
23. Ricardo Fitas, Gonçalo das Neves Carneiro, Carlos Conceição António. Swarm intelligence hybridized with genetic search in multi-objective design optimization under constrained-Pareto dominance. Composite Structures, 2023, vol. 319, p. 117155. https://doi.org/10.1016/j.compstruct.2023.117155.
24. Suresh P. V. S., Venkateswara Rao P., Deshmukh S. G. A genetic algorithmic approach for optimization of surface roughness prediction model. International Journal of Machine Tools and Manufacture, 2002, vol. 42, iss. 6, pp. 675-680. https://doi.org/10.1016/S0890-6955(02)00005-6.
25. Kuo-Hao Chang. Stochastic Nelder–Mead simplex method – A new globally convergent direct search method for simulation optimization. European Journal of Opera-tional Research, 2012, vol. 220, iss. 3, pp. 684-694. https://doi.org/10.1016/j.ejor.2012.02.028.
26. Kuo-Hao Chang. A direct search method for unconstrained quantile-based simulation optimization. European Journal of Operational Research, 2015, vol. 246, iss. 2, pp. 487-495. https://doi.org/10.1016/j.ejor.2015.05.010.
27. Abdel-Rahman Hedar, Masao Fukushima. Tabu Search directed by direct search methods for nonlinear global optimization. European Journal of Operational Research, 2006, vol. 170, iss. 2, pp. 329-349. https://doi.org/10.1016/j.ejor.2004.05.033.
28. Paresh Kumar Panigrahi, Sukanta Nayak. Numerical approach to solve imprecisely defined systems using Inner Outer Direct Search optimization technique. Mathematics and Computers in Simulation, 2024, vol. 215, pp. 578-606. https://doi.org/10.1016/j.matcom.2023.08.025.
29. Umesh Khandey, Vedpal Arya. Optimization of multiple surface roughness characteristics of mild steel turned product using weighted principal component and Taguchi method. Materials Today: Proceedings, 2023. https://doi.org/10.1016/j.matpr.2023.04.298.
30. Sidharthan S., Raajavignesh G., Nandeeshwaran R., Radhika N., Jojith R., Jeyaprakash N. Mechanical property analysis and tribological response optimization of SiC and MoS2 reinforced hybrid aluminum functionally graded composite through Taguchi's DOE. Journal of Manufacturing Processes, 2023, vol. 102, pp. 965-984. https://doi.org/10.1016/j.jmapro.2023.08.013.
31. Paramjit Singh Bilga, Sehijpal Singh, Raman Kumar. Optimization of energy consumption response parameters for turning operation using Taguchi method. Journal of Cleaner Production, 2016, vol. 137, pp. 1406-1417. https://doi.org/10.1016/j.jclepro.2016.07.220.
