from 01.01.2013 to 01.01.2024
Sevastop, Russian Federation
The problem of uncertainty of catamaran behavior during a storm is considered. The main danger of uncertainty lies in the magnitude of the roll by which the catamaran will deviate, since this can lead to adverse consequences with the cargo or the hull of the vessel. The study of this uncertainty is considered from two positions: the study of control actions in the implementation of the worst-case scenarios of unrest at the stage of selecting a control system and online forecasting of roll thresholds. A complex model of catamaran and external disturbances is used. External perturbations are obtained using a formative filter and linear approximation of the Pearson-Moskowitz spectrum, forces and moments. The study of the quality of management is carried out by calculating the most likely trajectories to the specified threshold states and then comparing them with each other. This calculation is performed by solving an optimization problem of the Lagrange-Pontryagin type with an action functional as a criterion and a complex catamaran model and external disturbances as a coupling equation. Using the methods of the theory of large deviations, estimates of the probabilities of movement to threshold values along the most likely trajectories are obtained. Using these estimates and comparing them with the current state of the catamaran made it possible to realize the forecast of risky situations. Examples of trajectories leading to threshold states are given for several cases of wind and heading angles of the vessel obtained with different control circuits. At the same time, it can be seen that depending on the control, fluctuations arise, which must be paid attention to when designing the control. An example of estimating the probability of movement to the threshold state during the rolling of the catamaran is given. The use of threshold state profiles allows not only to obtain useful information in the design of control systems, but also to improve the safety of navigation.
catamaran, pitching, external disturbances, prediction of risky situations, profile of threshold states, theory of large deviations
Введение
Все морские суда, морские технические сооружения, находящиеся в открытом море, подвергаются таким внешним возмущениям, как ветер, волны
и течения. Одним из важнейших факторов, влияющих на безопасную эксплуатацию судна, является возможность управлять им [1, 2]. Выбор управляющих контуров, исследование их предельных возможностей и запасов устойчивости – важные этапы проектирования систем управления судами.
Среди всех классов судов катамаран выделяется наличием двух одинаковых корпусов, что придает как положительные, так и отрицательные качества судну [3]. Например, катамаран, не имеющий достаточного удлинения, может совершать переворот через нос, но катамаран имеет большую площадь палубного пространства. Изучение восприимчивости судна к бортовой качке является важным этапом проектирования, потому что она влияет на сохранность груза и людей. Следует отметить, что через бортовую качку реализуются и другие нежелательные события, например параметрическая качка, возникающая в продольном к волнению движении [4, 5].
Основные подходы к уменьшению бортовой качки связаны с изучением разного типа управления [6–8]: ПИД, линейно-квадратичный, робастный и т. д., где исполнительным механизмом является руль и движительная установка. Изменением скорости движения судна или угла перекладки руля можно влиять на амплитуду качки. Не реже используют и специальные выдвижные успокоители качки и водометы [9, 10]. Но некоторая неопределенность и риск остаются.
Рисковая ситуация связана с неопределенностью будущего состояния катамарана. При ветро-волновых воздействиях есть вероятность исходов с такими негативными последствиями, как переворачивание судна, изломы и деформации, повреждение груза и т. п. [11]. Очевидно, что какие бы хорошие управляющие системы ни были, они могут уменьшить амплитуду воздействий, но не исключить их полностью. При этом вероятность возникновения рисковых ситуаций уменьшается, но не исчезает.
Реализация таких рисковых ситуаций ожидаема при наступлении штормовых условий. Поэтому в статье будет рассматриваться состояние моря 5, 6 баллов по шкале Бофорта и симулироваться комплексная модель катамарана и ветро-волновых воздействий. В параметры воздействий входят скорость ветра и курсовой угол судна на генеральное направление волны.
В данной статье будет рассмотрена методика прогноза рисковых ситуаций, основанная на знании наиболее вероятных реализаций опасных ситуаций, рассчитанных с использованием математической модели катамарана и внешних возмущений. Расчет наиболее вероятных траекторий выполняется с применением методов теории больших уклонений, симулирование качки – с помощью метода Рунге – Кутта 4 порядка.
Катамаран, управление и внешние возмущения
Катамаран представляет собой судно с двумя одинаковыми корпусами, которые соединены друг с другом палубой (рис. 1).
Рис. 1. Общий вид катамарана
Fig. 1. General view of the catamaran
В статье используется известная модель катамарана из [6, 9]. Этот катамаран соответствует судну, предназначенному для перевозки пассажиров, легковых и грузовых автомобилей. Размеры катамарана указаны в таблице
Размеры катамарана
Catamaran dimensions
|
Параметр |
Значение |
|
Длина, м |
90 |
|
Ширина, м |
25,96 |
|
Осадка, м |
2,6 |
|
Водоизмещение, т |
734,54 |
Катамаран, помимо главной движительной установки, обеспечен подводными крыльями для снижения амплитуды качки и закрылками для балансирования во время движения и выполнения перемещений при швартовке.
На рис. 2 приведена структурная схема [6, 9], на которой показано взаимодействие элементов катамарана (динамика объекта, контур управления по состоянию катамарана, исполнительные механизмы) и возмущений.
Рис. 2. Схема влияния управляющих сигналов от управления по состоянию xCat и возмущения xDistb на катамаран
Fig. 2. The scheme of the influence of control signals from xCat and disturbances xDistb on the catamaran
Считаем, что возмущения от ветровой волны воздействуют на судно посредством силы и момента, зависят от курсового угла. Дифференциальное уравнение, соответствующее такой схеме, описывается как
ẋ = Ax + B ξ(t), с н. у. x(0) = O(6×1), (1)
где 
– блочная матрица, включающая динамику катамарана с управлением и формирующий фильтр внешних возмущений; 
О6×1 – матрица из нулей размером в 6 строк и 1 столбец; ξ(t) – белый шум; 
– вектор состояния, xCat – вектор состояния катамарана, xDistb – вектор состояния формирующего фильтра возмущения.
Раскроем величины и способы получения каждого элемента уравнения и схемы.
Модель катамарана
Катамаран с системой уменьшения качки [6, 9] описывается в виде модели пространства состояния
(2)
где 
– вектор состояния, включающий, соответственно, скорость вертикальной качки, м/с, скорость дифферента, °/с, вертикальную качку, м, угол дифферента, °, скорость крена, °/с, угол крена, °;
– матрица системы катамарана с обратной связью, ACat – матрица объекта, BCat – матрица управления, K – матрица обратной связи; 
– вектор возмущений, включающий силу, Н, и момент, Н⋅м, действующие на корпус судна; yCat – вектор выхода; CCat – матрица выхода. Числовые значения матриц системы, управления, выхода получены с использованием гидродинамической теории сечений (англ. strip theory) [1, 2]:
CCat = I6×6, где In×m – единичная (n × m) матрица; матрица
обратной связи получена путем синтеза линейно-квадратичного регулятора с критерием
где Q – постоянная положительно-определенная матрица такого же размера, как и матрица A; u – управляющий сигнал; R – положительно-определенная симметричная матрица.
Такой регулятор позволяет уменьшить амплитуду качки путем создания сил (FWing и FClap) и моментов (MWing и MClap) с помощью подводных крыльев и подруливающих клапанов.
Модель внешних возмущений
Качка катамарана возникает в результате воздействия внешних сил и моментов, создаваемых морскими волнами. Имитация этих сил и моментов выполнена с помощью метода формирующего фильтра [12] (рис. 3).
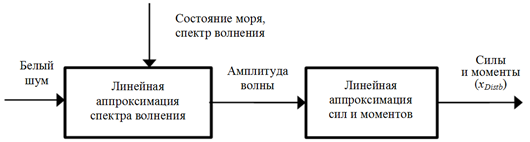
Рис. 3. Формирование возмущающих сил и моментов
Fig. 3. Formation of disturbing forces and moments
На вход фильтра подается белый шум, а на выходе получается вектор xDistb сил и моментов внешнего возмущения.
Формирующий фильтр состоит из двух частей. Первая – это линейная аппроксимация спектра Пирсона – Московица
где – частота. На рис. 4 показано сравнение спектра Пирсона – Московица с его линейной аппроксимацией.
Рис. 4. Спектр Пирсона – Московица в сравнении с его линейной аппроксимацией
Fig. 4. The Pearson – Moskowitz spectrum in comparison with its linear approximation
Вторая часть – это линейная аппроксимация сил и моментов с помощью коэффициента KFM. Все вместе можно представить в виде двух передаточных функций одинакового вида: с одинаковым входом, но выходами как сила и момент соответственно
где KFM = {KWaveForce, KWaveMoment} – параметр, характеризующий линейную аппроксимацию преобразования высоты волны в силу или в момент соответственно; Kω = 2λω0σ, λ – демпфирующий коэффициент, ω0 – доминирующая частота волнения,
– константа интенсивности волнения. Расчет коэффициентов λ, σ, ω0 возможен аналитически или численно, а выбор коэффициентов KWaveForce и KWaveMoment определяется путем многократного моделирования. Выбранные величины параметров соответствуют 5-му состоянию моря (по шкале Бофорта) со значительной высотой волн 2,14 м и средней скоростью ветра 10 м/с. Полученная в результате симуляции статистика качки соответствует таковой для соразмерных судов в этих погодных условиях и тому, что было показано авторами модели катамарана в статьях [6, 9], что говорит о том, что выбранные значения коэффициентов подходят.
Используя две эти передаточные функции, формируем модель в виде пространства состояний с матрицами
и вектором состояния
, где Mw – момент, Н⋅м; Fw – сила, Н; и получаем матрицу передачи возмущений в катамаран
.
Методика прогнозирования рисковых ситуаций
Получение наиболее вероятных траекторий может быть проведено с помощью метода Монте-Карло и его модификаций, но в данной статье воспользуемся теорией больших уклонений [13–15] и построим наиболее вероятную траекторию (НВТ) аналитически. Для этого в уравнение системы (1)
вводится малый параметр ε:
ẋ = Ax + εBξ(t), x(0) = x0, (3)
и решается задача минимизации для случая бесконечного слева времени
, (4)
где 
– квазипотенциал, который характеризует движение системы на большом интервале времени, на котором превышение порога xп точно произойдет; x* – это наиболее вероятная траектория движения из аттрактора
O к xп при воздействии малых случайных возмущений; 
– функционал действия, T – оператор транспонирования,
σ = B. Задача (4) имеет смысл, потому что для системы (3) известна из [13] оценка вероятности P пересечения траекторией φ области D xп:
В результате решения задачи (4) с уравнением связи (3) получаем НВТ x*, реализацию возмущения v* и квазипотенциал V* с вероятностью 
вдоль НВТ, которые объединяем в кортеж 
– профиль порогового состояния xп.
На практике профиль порогового состояния используется при проектировании и выборе управляющего воздействия, что будет показано в следующем разделе. Другой вариант использования этого результата состоит в реализации супервизора управлений. Соотнося текущее состояние системы xс с НВТ x* можно утверждать, что оценки вероятности и времени того, что система под воздействием случайных возмущений пересечет xп, будут близки к соответствующим величинам профиля:
; (5)
. (6)
Принимать решение о переключении управлений или сигнализации можно на основе текущей оценки времени или вероятности:
,
где 
– пороговые значения вероятности и времени. Уровень порога устанавливается эмпирически. Смысл этой оценки вероятности заключается в понимании вероятности наихудшего сценария развития событий: НВТ – это наихудший вариант для системы, потому что нежелательное событие реализуется наискорейшим образом. Малый параметр ε можно воспринимать как склонность к риску при принятии управляющих решений.
Профили пороговых состояний при синтезе управлений
При проектировании судна чаще всего исходят из свойств самого корпуса судна, а уже потом думают о системе управления, которая будет поддерживать это судно в заданном режиме. В этом разделе мы покажем, как ведет себя катамаран при реализации наихудших сценариев штормовых условий при разных управляющих контурах.
Для системы (1) была решена задача (3), (4) несколько раз для разных скоростей ветра и курсовом угле на ветер, в результате чего получены профили пороговых состояний крена в 8, 10 и 12º (рис. 5).
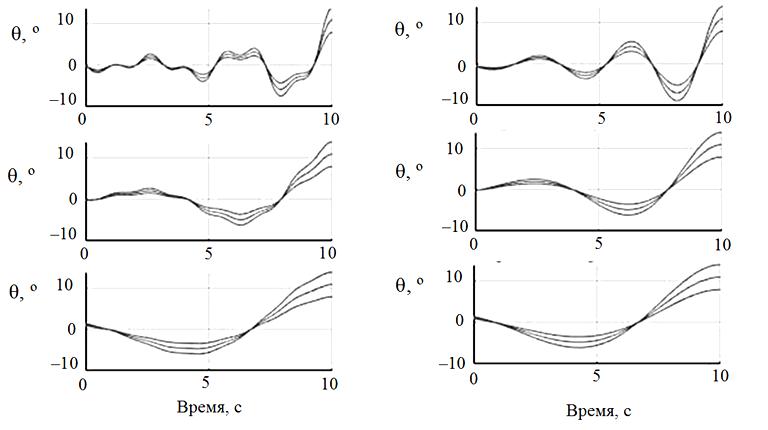
а б
Рис. 5. Траектории экстремальных значений крена для управления K: а – курсовой угол 45°; б – 0°;
верхний ряд – ветер – 5 м/с, средний – 10 м/с, нижний – 15 м/с
Fig. 5. Trajectories of extreme roll values for K control: a – heading angle 45°; б – 0°;
upper row – wind – 5 m/s, middle – 10 m/s, lower – 15 m/s
При разных значениях ветра и курса траектории имеют разную форму. Из-за симметричности корпуса эффект для левого и правого борта судна идентичен. Когда курсовой угол равен нулю, влияние соотношений крена, тангажа и дифферента значительно: формы траекторий искажены и «скачкообразны» (рис. 5, а). Когда курсовой угол равен 45º, влияние крена, тангажа и крена несущественно и траектории достаточно гладкие (рис. 5, б).
Первое наблюдение соответствует известной практике: во время шторма следует уменьшать курсовой угол. Другое наблюдение говорит о том, что слабый ветер требует много энергии для реализации большого крена, поэтому видна «раскачка» судна. Таким образом, необходимо следить, чтобы частота колебаний судна не совпала с собственной частотой колебаний судна.
Для сравнения на рис. 6 показаны те же самые величины для другой матрицы в управлении системой (2), равной
.
а б
Рис. 6. Траектории экстремальных значений крена для управления K2: а – курсовой угол 45°; б – 0°; верхний ряд – ветер – 5 м/с, средний – 10 м/с, нижний – 15 м/с
Fig. 6. Trajectories of extreme roll values for K2 control: a – heading angle 45°; б – 0°; upper row – wind – 5 m/s, middle – 10 m/s, lower – 15 m/s
Видно, что в этом случае движение к пороговым значениям происходит плавнее, что говорит об улучшении уровня комфорта.
Прогноз рисковых ситуаций
Рассмотрим результаты прогноза рисковых ситуаций с помощью профилей пороговых состояний, основанных на оценках времени , функционирования катамарана в штормовых условиях. Рассматриваемая рисковая ситуация будет состоять в достижении крена более чем 5º (основной порог), что будет означать неблагоприятные последствия.
Для системы (1) были получены профили пороговых состояний для крена от 1 до 11º. Применение нескольких профилей обусловлено тем, что движение к большим порогам происходит через пересечение маленьких, а наличие порогов выше основного порога позволит также выделить и основной порог.
С помощью метода Рунге – Кутта 4 порядка просимулировали систему (1), т. е. получили решение задачи Коши на интервале времени [0, TS] в дискретные моменты времени t0 = 0 ˂ t1 ˂ ... ˂ tend = TS,
с фиксированным шагом 
, где TS – длительность симуляции. В каждый момент времени tj инкремент шума 
. В результате получили реализацию качки катамарана, гистограммы которой показаны на рис. 7, а пример реализации на рис. 8.
Рис. 7. Гистограммы качки катамарана
Fig. 7. Histograms of catamaran pitching
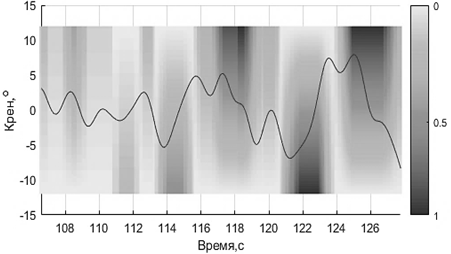
Рис. 8. Оценки вероятности наступления рисковых ситуаций с использованием нескольких профилей пороговых состояний
Fig. 8. Estimates of the probability of occurrence of risky situations using several profiles of threshold states
Затем для каждого момента времени по формулам (5) и (6) осуществили оценки времени и вероятности .
На рис. 8 показан участок траектории и оценки вероятности движения к заданному порогу: чем темнее, тем выше вероятность пересечь порог этого уровня. Так, например, прогноз вполне удачен в смысле предугадывания будущего пересечения основного порога для интервалов времени 114–117 с и 120–125 с и менее удачен для 118–120 с.
Обнаружение возможного пересечения порога действительно происходит заранее (на 1–1,5 с). Но сделать это еще раньше пока что затруднительно. Подтверждением этому может служить накопленная статистика качки. Рис. 9 показывает плотность траекторий крена (по оси абсцисс указан угол крена, °, по оси ординат – время, с, до пересечения порога в 4°): в большинстве случаев выход крена из области допустимых колебаний (около 3°) и пересечение порога происходит за менее чем 1 с. Эта статистика также служит и подтверждением результатов, изображенных на рис. 6.
Рис. 9. Плотность траекторий при движении к порогу в 4º крена
Fig. 9. The density of trajectories when moving to the threshold of 4º roll
Из рис. 6 и рис. 9 следует вывод о том, что при последующем решении задачи управления необходимо не только быстрое прогнозирование, но и столь же быстрое управление.
Заключение
Для комплексной модели качки катамарана и ветро-волновых возмущений были построены профили пороговых состояний, показывающие возможные наихудшие реализации большого крена. Профили пороговых состояний могут быть применены на этапе проектирования системы управления для оценки качества управляющего контура путем визуальной оценки качества переходных процессов и числовых значений величин возмущающих воздействий и критерия оптимизации. В результате симулирования комплексной модели качки катамарана и ветро-волновых возмущений было показано, что профили пороговых состояний могут быть использованы во время функционирования катамарана в штормовых условиях для оценки риска возникновения большого крена. Дальнейшее развитие этой методики прогнозирования связано с накоплением опыта применения на других моделях и увеличением окна прогноза.
1. Semenov-Tian-Shanskii V. V. Statika i dinamika korablia [Ship statics and dynamics]. Leningrad, Su-dostroenie Publ., 1973. 608 p.
2. Faltinsen O. M. Hydrodynamics of High-Speed Ma-rine Vehicles. Cambridge University Press, 2005. 454 p.
3. Manuel S. G. de la J., Joaquín A., María G.-S. J., Francisco V. Improving the comfort of a fast ferry. IEEE Control Systems Magazine, 2004, vol. 24 (2), pp. 47-60.
4. Vagushchenko L. L, Vagushchenko A. L., Zaichko S. I. Bortovye avtomatizirovannye sistemy kontrolia morekhodnosti [On-board automated seaworthiness control systems]. Odessa, Feniks Publ., 2005. 272 p.
5. Antonenko S. V., Kitaev M. V. Bortovaia kachka i dinamicheskaia ostoichivost' sudna [On-board pitching and dynamic stability of the vessel]. Vologdinskie chteniia. Vladivostok, Izd-vo Dal'nevostoch. feder. un-ta, 2004. No. 40. Pp. 54-60.
6. Liang L., Yuan J., Zhang S. Application of model predictive control technique for wave piercing catamarans ride control system. 2016 IEEE International Conference on Mechatronics and Automation. Harbin, 2016. Pp. 726-731.
7. Wang Y., Bai L., Liu S. Nonlinear control of hydro-foil catamaran course in three DOF. 2014 IEEE Conference and Expo Transportation Electrification Asia-Pacific (ITEC Asia-Pacific). Beijing, 2014. Pp. 1-6.
8. Kapitanyuk Y., Proskurnikov A., Cao M. Optimal controllers for rudder roll damping with an autopilot in the loop. IFAC-Papers Online, 2016, vol. 49, no. 23, pp. 562-567.
9. Zhang S., Li S., Liang L., Sun M. Ride control meth-od of wave-piercing catamaran with T-foil and flaps. IEEE International Conference on Mechatronics and Automation. Tianjin, 2014. Pp. 509-514.
10. Lukomskii Iu. A., Le Tkhan' Tung, Shpektorov A. G. Ispol'zovanie neirosetevykh tekhnologii pri postroenii sistem upravleniia dvizheniem skorostnykh sudov [The use of neural network technologies in the construction of high-speed vessel traffic control systems]. Izvestiia SPbGETU «LETI». Seriia: Avtomatizatsiia i upravlenie, 2006, iss. 1, pp. 14-18.
11. Vaganov A. B., Tan N. N. Dinamika sudna pri slozhnom vnezapnom vozdeistvii vneshnikh sil [Ship dynamics under complex sudden impact of external forces]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta. Seriia: Morskaia tekhnika i tekhnologiia, 2014, no. 4, pp. 13-20.
12. Fossen T. I. Handbook of marine craft hydrodynamics and motion control. Jhon Wiley & Sons, 2011. 600 p.
13. Venttsel' A. D., Freidlin M. I. Fluktuatsii v dinamicheskikh sistemakh pod deistviem malykh sluchainykh vozmushchenii [Fluctuations in dynamical systems under the action of small random disturbances]. Moscow, Nauka Publ., 1979. 424 p.
14. Dubovik S. A., Kabanov A. A. Funktsional'no ustoichivye sistemy upravleniia: asimptoticheskie metody sinteza [Functionally stable control systems: asymptotic synthesis methods]. Moscow, Infra-M Publ., 2019. 249 p.
15. Dubovik S. A., Kabanov A. A. Quasipotentials in synthesis of control system based on knowledge. International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM). Saint Petersburg, 2017. Pp. 1-4.
