Russian Federation
Russian Federation
Russian Federation
Russian Federation
In recent years, artificial intelligence technologies have demonstrated significant success in solving the problem of traffic analysis and forecasting in various telecommunication systems. Forecasting allows the telecom operator to know about the future behavior of the network, take timely necessary measures to improve the quality of customer service, and decide on the need to install or upgrade equipment. Using data collected from IoT mobile devices as an example, this article provides an overview and analysis of various time series forecasting models describing the traffic behavior of telecommunication systems. Forecasting models such as the exponential smoothing method, linear regression, the autoregressive integrated moving average (ARIMA) method, the support vector machine regression method, the N-BEATS method, which uses fully connected layers of a neural network for forecasting a one-dimensional time series, are discussed; the features of some of them are briefly outlined. For a specific data array, data preparation operations are described: removing unused columns, replacing missing data on transaction durations with their median values, and describing the main statistical characteristics of the data array. A preliminary data analysis is presented, which consists of using smoothing methods: moving average and exponential smoothing. The process of training models and a comparative analysis of the quality of their training are described. For this data set, it was concluded that for the UDP protocol the ARIMA model has the best learning quality, for the TCP protocol - linear regression and the Theta model, for the HTTPS protocol – linear regression, ARIMA and N-BEATS.
telecommunication systems, information traffic analysis, forecasting models, QoS, artificial intelligence, linear regression, ARIMA, Theta, N-BEATS
Введение
Постоянно растущий трафик в телекоммуникационных сетях подтверждает, что общество движется к миру, управляемому данными, это является естественным стимулом для развития сетей связи. Рыночный спрос выливается во множество технических требований, которым должны удовлетворять сети связи, что обязывает операторов, поставщиков технологий и услуг постоянно внедрять элементы инноваций в сетевую инфраструктуру и терминалы. Поэтапный отказ от старых сетей (например, 2G, 3G) постепенно приведет к переходу на новые технологии радиодоступа (особенно на растущих рынках) с последующим увеличением потребления трафика данных. Индустрия мобильной связи также должна перейти от традиционных стратегий к некоторым новым, таким как работа в совместно используемых диапазонах спектра [1], совместное использование спектра между операторами, сети малых сот внутри помещений, большое количество местных сетевых операторов и аренда сегмента сети по требованию. Ожидается, что трафик, потребляемый во всем мире, будет обслуживаться не только сотовыми сетями и эволюцией 5G. Wi-Fi-соединения постоянно улучшают свою надежность и производительность, особенно в помещениях, в то время как большая часть потребления сетевого трафика по-прежнему связана с вариантами использования внутри помещений и сценариями с ограниченной мобильностью (например, дома, в офисе, в торговом центре и т. д.). Чтобы удовлетворить эту потребность, стандарты уже поддерживают конвергенцию 5G/Wi-Fi на различных уровнях, даже если фактическая проработанность технических решений и связанная с ними терминальная поддержка еще не достигли уровня массового внедрения.
Прогнозирование – это статистический метод, используемый для извлечения более релевантной информации из большого объема данных и прогнозирования будущих результатов путем сбора и анализа текущих и прошлых событий. С увеличением числа операторов мобильной связи и доступа в Интернет трафик данных создает большие проблемы, поскольку нагрузка на сеть постоянно увеличивается. С увеличением объема больших сотовых данных прогнозирование трафика становится сложной задачей из-за временной и пространственной динамики, определяемой различным поведением пользователей. Точное прогнозирование трафика сотовой сети на базовой станции позволяет обеспечить хорошее качество услуг и играет важную роль в оптимизации, проектировании и моделировании управления телекоммуникационными сетями. В настоящее время исследование прогнозирования трафика 5G и долгосрочного развития 4G (LTE) играет важную роль в повышении качества обслуживания при передаче мультимедиа. Точное прогнозирование трафика мобильных данных полезно для прогнозирования регионального трафика, планирования городских районов и выбора места расположения базовой станции. Таким образом, анализ и прогнозирование сетевого трафика являются важной частью сотовых сетей для минимизации нагрузки, поскольку они используются для контроля и управления сетью. Структура сотового трафика на самом деле очень сложна из-за различных факторов, например мобильности пользователей, схемы прибытия и различных требований пользователей.
В последние годы прогнозирование трафика сотовой сети выполняется с использованием концепции глубокого обучения и статистического обучения [2, 3]. Прогнозирование трафика сотовой сети можно разделить на два класса прогнозов: краткосрочный и долгосрочный. Краткосрочные прогнозы позволяют осуществлять оперативное управление сетью связи, обеспечивая требуемое качество оказания услуг абонентам. Долговременное прогнозирование позволяет проводить стратегическое планирование по развитию сетей связи, внедрению новых технологий, обеспечению надежности сети.
Перспективным направлением решения описанных выше задач является адаптация технологий искусственного интеллекта (ИИ) для анализа и прогнозирования трафика сетей 5G, на основе сетевых данных. Технологии ИИ не только сократят ручное вмешательство в управление сетевым трафиком, но и позволят обеспечить более высокую производительность сети, более высокую надежность и более адаптивные системы за счет извлечения новой информации из сетей и прогнозирования условий сетевого трафика и поведения пользователей, что позволит принимать более разумные решения при минимальном участии человека.
Целью данного исследования является анализ эффективности различных моделей прогнозирования параметров трафика, а именно длительности транзакции, основывающихся на методах машинного обучения и нейросетевых методах. В частности, для анализа были выбраны модели экспоненциального сглаживания, линейная регрессия, метод авторегрессионного интегрированного скользящего среднего (ARIMA) и метод N-BEATS. Анализ эффективности моделей производился на датасете трафика устройств IoT, установленных на общественном транспорте. В качестве основного критерия эффективности обучения выступали средняя абсолютная процентная ошибка (англ. Mean Absolute Percentage Error, MAPE) и симметричная MAPE (англ. Simmetric MAPE, SMAPE).
Обзор моделей прогнозирования трафика
Анализ и прогнозирование трафика являются важными составляющими управления современными телекоммуникационными системами и сетями. На основе подобных прогнозов своевременно выделяются и резервируются ресурсы оборудования, необходимые для поддержания надлежащего качества оказания услуг. Проблемам точного прогнозирования трафика в проводных широкополосных сетях и сотовых сетях посвящено по крайней мере два направления исследований. Одно из них основано на подгонке моделей (например, on-off модель, модель ARIMA [4], модель FARIMA [5], модель мобильности [6], модель сетевого трафика [7] и альфа-стабильная модель [8]) для изучения характеристик трафика, таких как пространственная и временная релевантность или самоподобие [9], и получения будущего трафика с помощью соответствующих методов прогнозирования. Другое направление исследований основано на современных методах обработки сигналов (например, методе анализа основных компонентов, методе фильтрации Калмана [10] или методе сжатия [11]) для регистрации эволюции трафика.
В последнее время была проделана большая работа по исследованию динамических характеристик беспроводного трафика, в том числе с учетом их нестационарности и сезонности, для увеличения точности прогнозов [12–19]. Прогнозирование сотового трафика в этих работах можно рассматривать как задачу анализа временных рядов, производительность которой зависит от ее линейных статистических моделей, таких как авторегрессионная интегрированная скользящая средняя (ARIMA) и альфа-стабильная модель.
Метод экспоненциального сглаживания (Exponential Smoothing Method) был предложен Q. T. Tran и др. [12] для прогнозирования трафика сотовой сети; N. Sapankevych and R. Sankar [13] применили линейную регрессию (Linear Regression LR), а J. Wang с соавторами в работе [14] использовали регрессию машины опорных векторов (Support Vector Machine Regression – SVMR) для прогнозирования трафика сотовой сети.
В работе [15] обсуждаются способы повышения производительности системы QoS. Авторы используют модель ARIMA для периодических прогнозов трафика мобильной широкополосной связи (eMBB), а система QoS заранее резервирует каналы для прогнозируемых потоков eMBB, чтобы максимизировать общий объем трафика. Этим обеспечивается оптимальная скорость передачи данных от источников до пунктов назначения.
В исследовании [16], основанном на данных о трафике IP-сети из тридцати одной провинции Китая, прогнозирование производилось с использованием комбинации модели ARIMA и модели N-BEATS. Эффективность прогнозирования оценивалась по трем показателям: MAPE, среднеквадратическая ошибка (англ. Root Mean Squared Error, RMSE) и средняя абсолютная ошибка (англ. Mean Absolute Error, MAE). Результаты исследования показали, что комбинирование N-BEATS и ARIMA дает хорошие результаты при прогнозировании показателей трафика IP-сети.
Работа [17] также рассматривает прогнозирование трафика мобильных сетей на основе анализа реальных данных, собранных China Mobile Communications Corporation (CMCC). В данной статье предлагается использовать сезонные модели ARIMA для прогнозирования трафика мобильной связи. Эксперименты и результаты испытаний показали довольно высокую эффективность такого подхода.
В статье [18] рассматривается модель дискретного вейвлет-преобразования (DWT), ARIMA и метод на основе рекуррентной нейронной сети (RNN) для прогнозирования трафика компьютерной сети. Трафик компьютерной сети отбирался на сетевом устройстве, подключенном к Интернету. Дискретное вейвлет-преобразование используется для разложения данных трафика на нелинейные и линейные компоненты. После этого компоненты реконструируются с использованием обратного преобразования, а прогнозы делаются с использованием ARIMA. Такое прогнозирование очень полезно для многочисленных приложений, таких как контроль перегрузки, обнаружение аномалий и распределение полосы пропускания. Такой метод может применяться в центрах обработки данных, улучшая качество обслуживания (QoS) и снижая затраты.
Исследование [19] направлено на сравнение модели временных рядов ARIMA и K-средних применительно к прогнозированию нагрузки облачной инфраструктуры. В работе отмечается, что хотя для обработки модели временных рядов ARIMA требуется больше времени, чем для K-средних, ее целесообразно использовать, когда необходимы более детальная характеристика и изучение рабочей нагрузки кластера.
Подготовка данных
Данные были собраны с мобильных устройств, установленных в кооперативной интеллектуальной транспортной системе (C-ITS) Швеции. Датасет был сформирован из данных, пересылаемых автобусами на точки сбора данных IoT, и включает в себя 44 844 строк записи с 40 столбцами категорий. Среди 40 категорий, многие из которых не значимы для данного исследования, следует выделить такие важные категории, как:
– Index – уникальный номер транзакции;
– Timestamp – временная метка начала транзакции (дата и время);
– TransactionTime – время транзакции (в секундах);
– protocol – используемый протокол (UDP, TCP или HTTPS).
Для быстрой визуальной оценки отсутствующих данных построена диаграмма (рис. 1), на ней белым цветом отмечены отсутствующие данные.

Рис. 1. Диаграмма, иллюстрирующая отсутствующие данные (отображаются белым цветом)
Fig. 1. Chart illustrating missing data (shown in white)
Для интересующих нас столбцов процент отсутствующих данных составляет: Index – 0 %, Timestamp – 0 %, TransactionTime – 3 %, protocol – 0 %.
Недостающие данные TransactionTime были дополнены медианным значением (равным 0.305502 с), рассчитанным по столбцу TransactionTime.
При анализе данных важно определить данные, которые сильно отличаются от большинства (outliers – «выбросы»). В данном случае наиболее интересны данные о времени транзакции: существуют ли «выбросы», и являются ли эти данные аномальными. Построим столбчатую диаграмму, иллюстрирующую данные о времени транзакций TransactionTime (рис. 2).
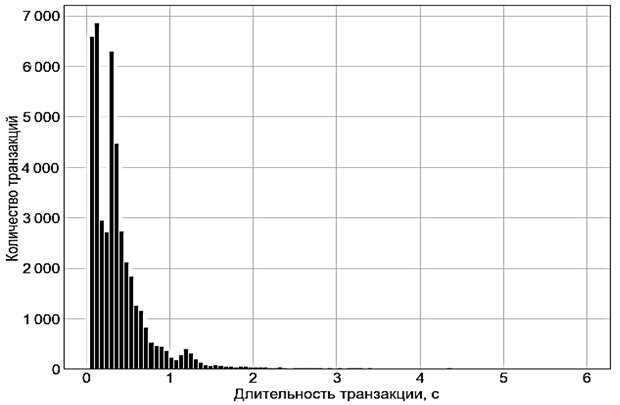
Рис. 2. «Выбросы» данных времени транзакций (хвост диаграммы)
Fig. 2. “Outliers” of transaction duration data (tail of the diagram)
Более наглядно аномальные данные представлены на диаграмме box plot (рис. 3).
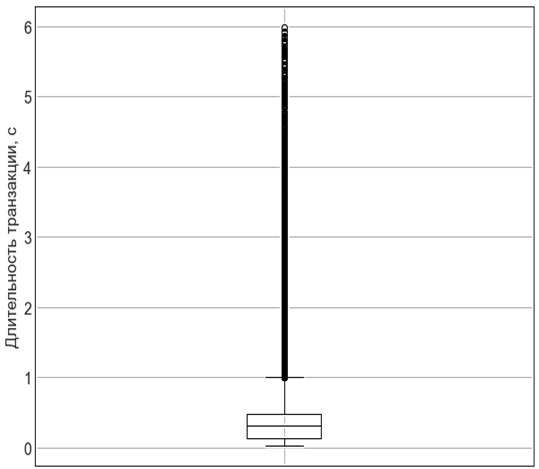
Рис. 3. Диаграмма box plot
Fig. 3. Box plot diagram
Диаграмма «ящик с усами» (box plot) является графическим методом визуализации распределения данных. В данном случае эта диаграмма наглядно иллюстрирует, что большее число транзакций имеет длительность от десятых долей секунды до примерно полсекунды, а транзакции, имеющие длительность примерно больше 1 с, уже являются относительно редкими в этом датасете. Box plot (см. рис. 3) состоит из «коробки», «усиков» и точек. Коробка показывает интерквартильный размах распределения, т. е., соответственно, 25 % (Q1) и 75 % (Q3) перцентили. Черта внутри коробки обозначает медиану распределения. Усы отображают весь разброс точек, кроме выбросов, т. е. минимальные и максимальные значения, которые попадают в промежуток (Q1 – 1,5 × IQR, Q3 + 1,5 × IQR), где IQR = Q3 – Q1 – интерквартильный размах, а × – знак умножения. Точками на графике обозначаются выбросы – те значения, которые не вписываются в промежуток значений, заданный усами графика (на рис. 3 это заметно для транзакций с длительностью от 1 до 6 с). Проанализируем описательную статистику по представленным данным (табл. 1).
Таблица 1
Table 1
Описательная статистика датасета
для признака TransactionTime
Descriptive statistics of the dataset
for the TransactionTime characteristic
|
Показатель |
Значение |
|
Среднее значение |
0,413150 |
|
Стандартное отклонение |
0,509285 |
|
Минимальное значение |
0,033924 |
|
Квартиль 25 % |
0,129970 |
|
Квартиль 50 % |
0,305502 |
|
Квартиль 75 % |
0,480927 |
|
Максимальное значение |
5,982710 |
Так, например, для признака TransactionTime 5,98 – максимальное значение, в то время как 75 % квартиль равен только 0,48. Однако значение транзакции в 5,98 с не является выбросом – это вполне реалистичное время для некоторых транзакций. Тем не менее возможно, что при обучении модели эти данные целесообразно отбросить.
Хотя сбор данных и производился три месяца, он производился нерегулярно, и поэтому дальнейший анализ возможен лишь для отдельных серий данных, соответствующих дням сбора информации. Например, на 13 декабря динамика изменения длительности транзакций в течение дня с учетом использовавшегося протокола выглядит следующим образом (рис. 4).
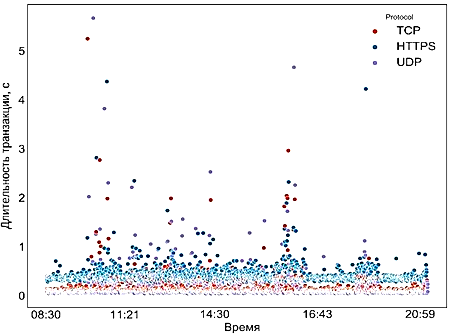
Рис. 4. Динамика изменения длительности транзакций
в течение дня с учетом использовавшегося протокола
Fig. 4. Dynamics of changes in the duration of transactions during the day, taking into account the protocol used
На графике, изображенном на рис. 4, прослеживаются тенденции, связывающие используемый протокол с временем транзакции – плотные скопления точек. Заметны и выбросы – отдельные точки, расположенные далеко от скоплений.
Предварительный анализ данных
Для анализа и краткосрочного прогнозирования ограничимся одним часом трафика, собранного в один из дней, при этом будем считать, что протокол передачи неважен.
Особенность данных трафика состоит в том, что полученные данные нерегулярны – в одни временные промежутки собирается большое количество данных, в другие транзакции отсутствуют и записей нет. Таким образом, из потока этих данных образуется нерегулярный временной ряд. Для работы с такими рядами они должны быть приведены
к регулярным рядам путем агрегации данных на временных участках, взятых с определенной частотой. В данном случае была выбрана частота временного ряда в 10 с, а в качестве агрегатора – среднее время транзакции за это время. В случае если за это время не было ни одной транзакции, среднее время было равно нулю (при прогнозировании будущих значений ряда иногда целесообразно считать его очень малым, но не нулевым, или интерполировать его по соседним значениям). Анализировать будем средние значения времени транзакции по десятисекундный промежуток времени. Для сглаживания данных применяется множество методов. Одним из популярных методов является сглаживание с помощью скользящего среднего. На рис. 5 и 6 представлены графики сглаживания для окон в 30 и 60 с (шкала времени представлена в формате «часы : минуты»).
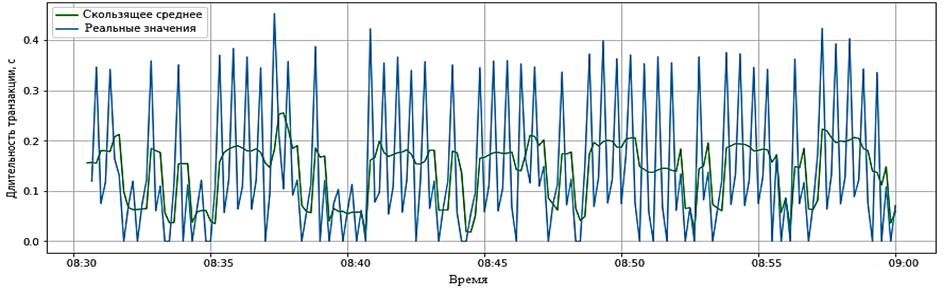
Рис. 5. Сглаживание данных с помощью скользящего среднего (размер окна 30 с)
Fig. 5. Smoothing data using moving average (window size 30 s)
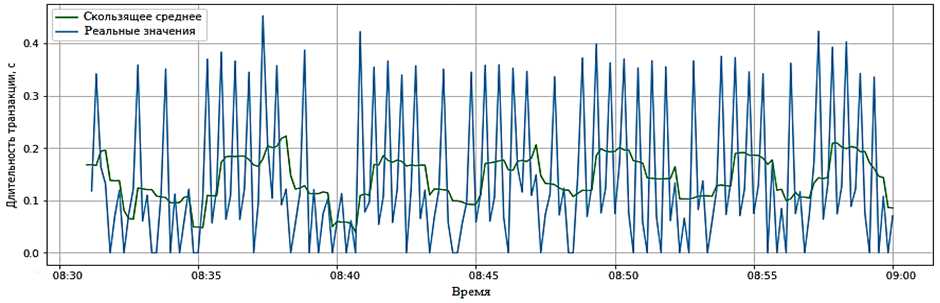
Рис. 6. Сглаживание данных с помощью скользящего среднего (размер окна 60 с)
Fig. 6. Smoothing data using moving average (window size 60 s)
Другим методом сглаживания данных является экспоненциальное сглаживание. Для этого метода основным параметром сглаживания является коэффициент α (может принимать значения от 0 до 1). Он определяет вес последнего наблюдения при вычислении прогноза. Выбор значения α влияет на скорость реакции на изменения в данных и степень сглаживания шумов. Маленькие значения α делают метод более устойчивым к шумам, но менее чувствительным к изменениям тренда и сезонности. Большие значения α делают метод более чувствительным к последним данным, но и более подверженным шумам. Для различных значений α график сглаживания представлен на рис. 7 (шкала времени представлена в десятках секунд).
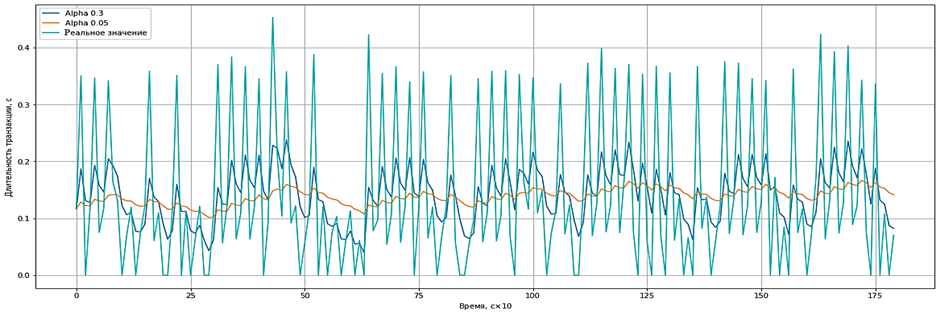
Рис. 7. Экспоненциальное сглаживание данных
Fig. 7. Exponential data smoothing
Обучение моделей и прогнозирование трафика
Экспоненциальное сглаживание и модели ARIMA являются двумя наиболее широко используемыми подходами к прогнозированию и представляют собой мощный инструмент при работе с временными рядами [20]. В то время как модели экспоненциального сглаживания основаны на описании тренда и сезонности данных, модели ARIMA направлены на описание автокорреляций в данных временного ряда.
Модель ARIMA состоит из автокорреляционной части (модель AR), которая представлена формулой
![]()
где yt – значения временного ряда в момент времени t; φ0, φ1, φ2, ..., φp – коэффициенты автокорреляции, которые определяют связь между текущим значением и предыдущими значениями ряда; ![]() – значения временного ряда в моменты времени t – 1, t – 2, ..., t – p соответственно; ɛt – случайное возмущение, описывающее влияние переменных, не учтенных в модели.
– значения временного ряда в моменты времени t – 1, t – 2, ..., t – p соответственно; ɛt – случайное возмущение, описывающее влияние переменных, не учтенных в модели.
Модель со скользящим средним (модель MA) порядка q задается уравнением
![]()
где ɛt – текущая ошибка (случайный шум); ɛt–1, ɛt–2, ..., ɛt–q – значения остатков i временных периодов назад (предыдущие ошибки); θ1, θ2, ..., θq – коэффициенты скользящего среднего, которые определяют влияния предыдущих ошибок на текущее значение временного ряда.
Модели скользящего среднего прогнозируют значения функции на основе линейной комбинации ограниченного числа q остатков, авторегрессионные же модели прогнозируют значения, используя линейную функцию аппроксимации ограниченного числа p прошлых значений.
Модель ARIMA (модель Бокса – Дженкинса) объединяет эти модели:
![]()
где с – константа.
Модель ARIMA (p, q, d) имеет три параметра:
– p – порядок авторегрессии. Он позволяет ответить на вопрос, будет ли очередной элемент ряда близок к значению X, если к нему были близки p предыдущих значений;
– q – порядок скользящего среднего. Позволяет установить погрешность модели как линейную комбинацию наблюдавшихся ранее значений ошибок;
– d – порядок интегрирования. Он показывает, насколько элемент ряда близок по значению к d предыдущим значениям, если разность между ними минимальна.
Многие из моделей являются частными случаями [19] модели ARIMA:
– белый шум – модель ARIMA (0, 0, 0) без константы;
– случайное блуждание – модель ARIMA (0, 1, 0) без константы;
– случайное блуждание с дрейфом – модель ARIMA (0, 1, 0) с константой;
– авторегрессия – модель ARIMA (p, 0, 0);
– скользящее среднее – модель ARIMA (0, 0, q);
До момента обучения модели необходимо убедиться, что временной ряд является стационарным. Стационарный временной ряд – это такой ряд, статистические свойства которого не зависят от времени наблюдения за этим рядом. Стационарность ряда определяется критерием Дики – Фуллера [21].
В данном случае он равен 0,001655 и ряд можно считать стационарным.
Для автоматического подбора [22] параметров модели использовалась функция auto_arima из библиотеки pmdarima. Наилучшими параметрами модели стали параметры (3, 0, 0), и представленная модель имеет авторегрессионный характер. На рис. 8 представлены график обучения и краткосрочный прогноз длительности транзакции вне зависимости от используемого протокола передачи.
Для анализа данных и прогноза длительности транзакций данные были разделены по отдельным протоколам: TCP, UDP, HTTPS. Для анализа и прогноза использовались следующие модели: наивная сезонная, экспоненциальное сглаживание, линейная регрессия, ARIMA, Theta и N-BEATS. Обзор большинства моделей приведен, например, в [23]. В качестве инструмента была использована библиотека Darts (для языка программирования Python). Она поддерживает различные подходы к прогнозированию временных рядов: от классических статистических моделей, таких как ARIMA и экспоненциальное сглаживание, до методов, основанных на машинном и глубоком обучении. Помимо этого библиотека Darts включает в себя функции анализа статистических свойств временных рядов, а также оценки точности моделей прогнозирования.
Наивная сезонная модель, как следует из названия, является довольно простой: она повторяет несколько последних значений временного ряда. При удачном подборе этих значений модель, несмотря на простоту, может давать неплохие результаты.
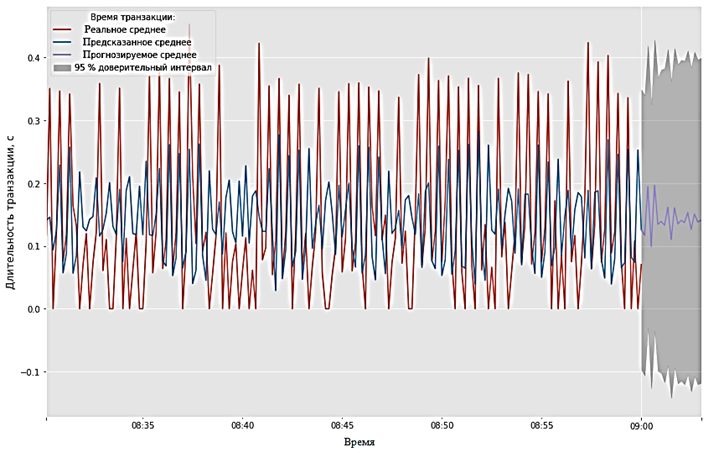
Рис. 8. График обучения модели ARIMA и краткосрочный прогноз длительности транзакции
Fig. 8. ARIMA model training schedule and short-term transaction duration forecast
Ранее уже упоминавшееся экспоненциальное сглаживание – одна из самых популярных моделей как для сглаживания данных, так и для прогнозирования временных рядов. Этот метод был разработан Брауном и Холтом, и в его основе лежит расчет экспоненциальных скользящих средних сглаживаемого ряда.
Линейная регрессия также является одной из часто используемых моделей. Ее достоинствами являются относительная простота и, как следствие, хорошая скорость обработки данных и прогнозирования. Зачастую это является определяющей характеристикой при использовании этой модели.
Тета-метод, разработанный Ассимакопулосом и Николопулосом, находит все большее применение при прогнозировании временных рядов. Подробное описание метода представлено в работе [24], а его модификация обсуждается в работе [25]. Этот метод особенно хорошо показал себя в соревновании M3 [26] и поэтому представляет интерес для практиковорогнозистов.
Метод N-BEATS [27] относится к методам прогнозирования с использованием нейронных сетей. Архитектура нейронной сети N-BEATS использует не рекуррентные, а полносвязные слои и наиболее эффективно применяется для одномерных временных рядов (рис. 9).
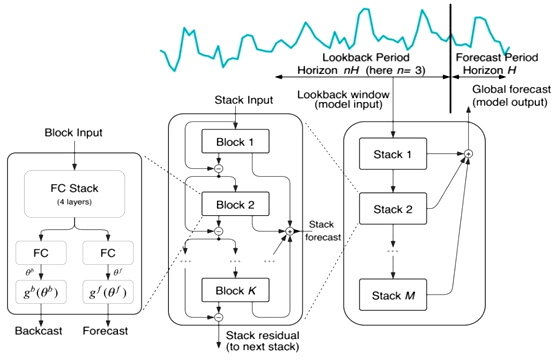
Рис. 9. Архитектура нейронной сети N-BEATS
Fig. 9. N-BEATS neural network architecture
Архитектура N-BEATS состоит из двух основных блоков: блоков «прогнозирования» (Forecast) и блоков «обновления» (Backcast). Блок прогнозирования отвечает за прогнозирование будущих значений временного ряда. Каждый такой блок состоит из нескольких полносвязных слоев (FS – fully connected layers) и слоев нормализации. Блок обновления, напротив, используется для обновления предсказания, основываясь на предыдущих значениях временного ряда. Он также состоит из полносвязных слоев и слоев нормализации. Блоки обновления служат для коррекции ошибок предсказаний, вносящихся в процессе прогнозирования. В сети N-BEATS временной ряд подается на вход, и сеть пропускает его через несколько полносвязных слоев. При этом выход данных с последнего слоя разделяется на две части: часть Backcast и часть Forecast. Эту структуру называют блоком (Block) сети. Выход Backcast вычитается из входного вектора перед следующим блоком, а выход Forecast прибавляется к вектору прогноза от предыдущего блока. Такая структура сети позволяет части Backcast отфильтровать только необходимую информацию из входных данных, а части Forecast скорректировать прогноз и уменьшить ошибку. Последовательность блоков называется стеком (Stack). Выходы со всех стеков суммируются, и таким образом вырабатывается глобальный прогноз.
В качестве показателей качества обучения моделей использовались следующие метрики [23]:
– средняя абсолютная ошибка (MAE);
– корень из средней квадратичной ошибки (RMSE);
– средняя абсолютная процентная ошибка (MAPE);
– симметричная MAPE (SMAPE).
Для протокола UDP наиболее подходящей моделью стала модель ARIMA. Прогнозирование длительности транзакций UDP с помощью метода ARIMA представлено на рис. 10.
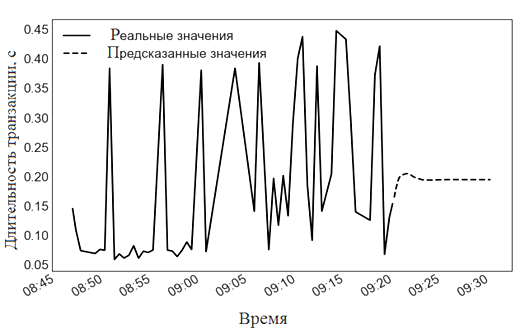
Рис. 10. Прогнозирование длительности транзакций UDP с помощью метода ARIMA
Fig. 10. Predicting of UDP transaction duration using the ARIMA method
Для протокола CP выбирается линейная регрессия и модели Theta (рис. 11, 12).
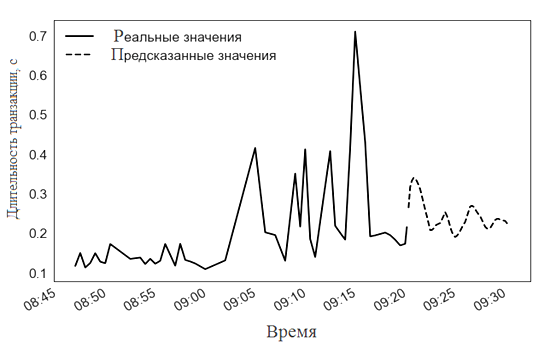
Рис. 11. Прогнозирование длительности транзакций TCP линейной регрессией
Fig. 11. Predicting TCP transaction duration using linear regression
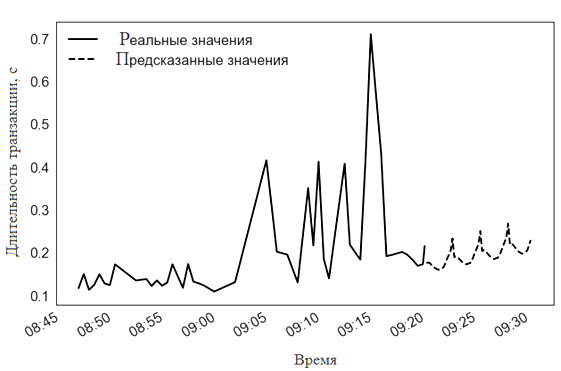
Рис. 12. Прогнозирование длительности транзакций TCP моделью Theta
Fig. 12. Prediction of TCP transaction duration by the Theta model
Для протокола HTTPS – линейная регрессия, ARIMA и N-BEATS (рис. 13).
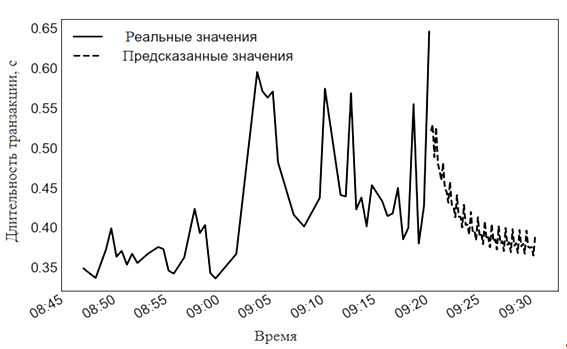
Рис. 13. Прогнозирование длительности транзакций HTTPS моделью N-BEATS
Fig. 13. Forecasting the HTTPS transaction duration using the N-BEATS model
Сравнительный анализ метрик качества обучения представлен в табл. 2.
Таблица 2
Table 2
Значения метрик качества обучения моделей
Values of metrics for the training models quality
|
Модель |
Метрика |
||||||
|
MAE |
RMSE |
MAPE |
SMAPE |
||||
|
Протокол UDP |
|||||||
|
Наивная сезонная |
0,0910 |
0,1242 |
56,4889 |
44,5716 |
|||
|
Экспоненциальное сглаживание |
0,0607 |
0,0834 |
32,1989 |
41,5392 |
|||
|
Линейная регрессия |
0,0512 |
0,0599 |
30,5981 |
27,4312 |
|||
|
ARIMA |
0,0466 |
0,0550 |
27,9993 |
25,1173 |
|||
|
Theta |
0,2794 |
1,0059 |
185,8544 |
63,7469 |
|||
|
N-BEATS |
0,0585 |
0,0663 |
35,4984 |
30,8297 |
|||
Окончание табл. 2
Ending of the table 2
|
Модель |
Метрика |
||||||
|
MAE |
RMSE |
MAPE |
SMAPE |
||||
|
Протокол TCP |
|||||||
|
Наивная сезонная |
0,0647 |
0,1011 |
23,0194 |
24,0684 |
|||
|
Экспоненциальное сглаживание |
1,2578 |
1,4767 |
604,3389 |
127,4042 |
|||
|
Линейная регрессия |
0,0344 |
0,0482 |
13,2520 |
13,1049 |
|||
|
ARIMA |
0,0742 |
0,0801 |
32,0026 |
28,6844 |
|||
|
Theta |
0,0582 |
0,1003 |
18,5042 |
22,9805 |
|||
|
N-BEATS |
0,0645 |
0,0957 |
22,9030 |
25,3388 |
|||
|
Протокол HTTPS |
|||||||
|
Наивная сезонная |
0,0845 |
0,1035 |
16,7633 |
17,5413 |
|||
|
Экспоненциальное сглаживание |
2,4104 |
2,7390 |
527,2670 |
130,8127 |
|||
|
Линейная регрессия |
0,0546 |
0,0679 |
11,3512 |
11,4193 |
|||
|
ARIMA |
0,0658 |
0,0779 |
14,8398 |
13,4941 |
|||
|
Theta |
0,0968 |
0,1134 |
21,6294 |
18,7798 |
|||
|
N-BEATS |
0,0777 |
0,0911 |
15,3963 |
16,9991 |
|||
При краткосрочном прогнозировании важным фактором является время, затрачиваемое на обработку данных: чем меньше времени и вычислительных мощностей требуется для работы модели, тем лучше. С этой позиции относительно простые модели, например линейная регрессия, метод скользящего среднего или наивная модель, более предпочтительны по сравнению со сложными моделями (ARIMA, N-BEATS), если обеспечивают приемлемое качество прогноза.
Заключение
Прогнозирование параметров трафика современных телекоммуникационных систем имеет большое значение для их развития и предоставления качественных услуг абонентам. На основе подобных прогнозов происходит выделение ресурсов системы: проводных и радиоканалов, полосы частот, производится автоматическая реконфигурация оборудования в случае сбоев или при внедрении новой аппаратуры связи.
Сравнительный анализ различных моделей обучения позволяет сделать следующие выводы: для протокола UDP для исследуемого временного ряда наиболее подходящей моделью стала модель ARIMA, для протокола TCP – линейная регрессия и модель Theta, для протокола HTTPS – линейная регрессия, ARIMA и N-BEATS. Качество обучения моделей и качество прогнозирования сильно зависит от исходного временного ряда, качества и полноты собранных данных. Зачастую относительно простые методы, такие как наивная сезонная модель или линейная регрессия, дают приемлемое качество краткосрочного прогноза, имея при этом значительно большее быстродействие, нежели сложные и более точные модели.
1. Pishchin O. N., Voronina K. P., Mal'tseva N. S. Modernizatsiia aviatsionnoi sistemy radiosviazi s tsel'iu povysheniia pomekhozashchishchennosti radiokanala [Modernization of the aviation radio communication system in order to increase the noise immunity of the radio channel]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta. Seriia: Upravlenie, vychislitel'naia tekhnika i informatika, 2023, no. 1, pp. 83-90. DOI:https://doi.org/10.24143/2073-5529-2023-1-83-90.
2. Rizvi S. Unveiling the Potential of Artificial Intelli-gence and Machine Learning in the 5G Network Landscape: A Comprehensive Review. AJRCoS, 2023, vol. 16, no. 4, pp. 23-31. DOI:https://doi.org/10.9734/ajrcos/2023/v16i4367.
3. Ahmadzai F. H., Lee W. A mobile traffic load prediction based on recurrent neural network: A case of telecommunication in Afghanistan. Electronics Letters, 2022, vol. 58, no. 14, pp. 563-565. DOI:https://doi.org/10.1049/ell2.12534.
4. Zhou B., He D., Sun Z., Ng W. H. Network traffic modeling and prediction with ARIMA/GARCH. Proc. HET- NETs’ 06 Conference (Ilkley, UK, 11-13 September 2006). Pp. 1-10.
5. Sarre O., Moulines E., Pesquet J.-C., Petropulu A. P., Xueshi Y. Long-range dependence and heavy-tail modeling for teletraffic data. IEEE Signal Process. Mag., 2002, vol. 19, no. 3, pp. 14-27.
6. Ashtiani F., Salehi J. A., Aref M. R. Mobility model-ing and analytical solution for spatial traffic distribution in wireless multimedia networks. IEEE J. Select. Area. Comm., 2003, vol. 21, no. 10, pp. 1699-1709.
7. Tutschku K., Tran-Gia P. Spatial traffic estimation and characterization for mobile communication network design. IEEE J. Select. Area. Comm., 1998, vol. 16, no. 5, pp. 804-811.
8. Ge M. X., Yu S., Yoon W.-S., Kim Y.-D. A new prediction method of alpha-stable processes for self-similar traffic. Proc. IEEE Globecom (29 November 2004 - 03 December 2004, Dallas, Texas, USA), 2004. DOI:https://doi.org/10.1109/GLOCOM.2004.1378047.
9. Leland W. E., Taqqu M. S., Willinger W., Wilson D. V. On the self-similar nature of Ethernet traffic. IEEE/ASM Trans. Netw., 1994, vol. 2, no. 1, pp. 1-15.
10. Falvo M. C., Gastaidi M., Nardecchia A., Prudenzi A. Kalman filter for short-term load forecasting: An hourly predictor of municipal load. Proc. Conference: The 16th IASTED International Conference on Applied Simulation and Modelling. 2007. Pp. 364-369.
11. Chen Y.-C., Qiu L., Zhang Y., Xue G., Hu Z. Robust network compressive sensing. Proc. ACM Mobicom 2014, Maui, Hawaii, USA, 2014. DOI:https://doi.org/10.1145/2639108.2639129.
12. Tran Q. T., Hao L., Trinh Q. K. Cellular network traffic prediction using exponential smoothing methods. J. Inf. Commun. Technol., 2019, vol. 18, no. 1, pp. 1-18.
13. Sapankevych N., Sankar R. Time series prediction using support vector machines: a survey. IEEE Computa-tional Intelligence Magazine, 2009, vol. 4, no. 2, pp. 24-38.
14. Wang J., Wang Ya., Zhang X., Tang J., Xue G., Xu Zh., Yang D. Spatiotemporal modeling and prediction in cellular networks: a big data enabled deep learning approach. Proceedings of the IEEE INFOCOM 2017, IEEE Conference on Computer Communications, Atlanta, GA, USA, May 2017. DOI:https://doi.org/10.1109/INFOCOM.2017.8057090.
15. Akcapinar A., Gurer O., Rodoplu V. ARIMA-Based Traffic Forecasting for Quality of Service (QoS) Flow Routing in Sixth Generation (6G) Networks. 2022 Innovations in Intelligent Systems and Applications Conference (ASYU), Antalya, Turkey: IEEE, Sep. 2022. Pp. 1-5. DOI:https://doi.org/10.1109/ASYU56188.2022.9925365.
16. Deng L., Ruan K., Chen X., Huang X., Zhu Y., Yu W. An IP Network Traffic Prediction Method based on ARIMA and N-BEATS. 2022 IEEE 4th International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China: IEEE, Jul. 2022. Pp. 336-341. DOI:https://doi.org/10.1109/ICPICS55264.2022.9873564.
17. Guo J., Peng Y., Peng X., Chen Q., Yu J., Dai Y. Traffic forecasting for mobile networks with multiplicative seasonal ARIMA models. 2009 9th International Conference on Electronic Measurement & Instruments, Beijing, China: IEEE, Aug. 2009. Pp. 3-377-3-380. DOI:https://doi.org/10.1109/ICEMI.2009.5274287.
18. Madan R., Mangipudi P. S. Predicting Computer Network Traffic: A Time Series Forecasting Approach Using DWT, ARIMA and RNN. 2018 Eleventh International Conference on Contemporary Computing (IC3), Noida: IEEE, Aug. 2018. Pp. 1-5. DOI:https://doi.org/10.1109/IC3.2018.8530608.
19. Mishra V. K., Mishra M., Tekale S., Praveena T. N., Venkatesh R., Dewangan B. K. ARIMA time Series Model vs. K-Means Clustering for Cloud Workloads Performance. 2022 OPJU International Technology Conference on Emerging Technologies for Sustainable Development (OTCON), Raigarh, Chhattisgarh, India: IEEE, Feb. 2023. Pp. 1-6. DOI:https://doi.org/10.1109/OTCON56053.2023.10113979.
20. Tregub A. V., Tregub I. V. Metodika postroeniia modeli ARIMA dlia prognozirovaniia dinamiki vremennykh riadov [The technique of constructing the ARIMA model for predicting the dynamics of time series]. Vestnik Moskovskogo gosudarstvennogo universiteta lesa - Lesnoi vestnik, 2011, no. 5, pp. 179-183.
21. Hyndman R. J., Athanasopoulos G. Forecasting: Principles and Practice. Australia, OTexts, 2021. Available at: https://otexts.com/fpp3 (accessed: 01.11.2023).
22. Nielsen A. Practical time series analysis: prediction with statistics and machine learning. Sebastopol, CA, O’Reilly Media, Inc, 2019. 504 p.
23. Tsihrintzis G. A., Virvou M., Jain L. C. Advances in Machine Learning/Deep Learning-based Technologies. Springer International Publishing, 2022. DOI:https://doi.org/10.1007/978-3-030-76794-5.
24. Assimakopoulos V., Nikolopoulos K. The theta model: a decomposition approach to forecasting. International journal of forecasting, 2000, vol. 16, no. 4, pp. 521-530.
25. Hyndman R. J., Billah B. Unmasking the Theta method. International Journal of Forecasting, 2003, vol. 19, no. 2, pp. 287-290. DOI:https://doi.org/10.1016/S0169-2070(01)00143-1.
26. Makridakis S., Hibon M. The M3-Competition: re-sults, conclusions and implications. International Journal of Forecasting, 2000, vol. 16, no. 4, pp. 451-476. DOI:https://doi.org/10.1016/S0169-2070(00)00057-1.
27. Oreshkin B. N., Carpov D., Chapados N., Bengioet Y. N-BEATS: Neural basis expansion analysis for interpretable time series forecasting. Available at: arXiv preprint arXiv:1905.10437 (accessed: 28.10.2023).















