Russian Federation
Russian Federation
Russian Federation
Russian Federation
The article highlights the application of the principle of achieving the best guaranteed result in the tasks of assessing the qualifications of the ship crew members in performing their official duties (based on the use of a program for monitoring the actions of ship specialists aimed at solving navigation problems, under the influence of various negative factors - disturbances) are discussed. The case is considered when the disturbance acts on several controlled indicators at once (current constraints, final conditions, quality criterion). During the implementation of the monitoring program, the reaction of the crew members to a specific disturbance is evaluated (at the same time, only a set of possible disturbances is assumed to be known). The developed management program is able to guarantee a reliable assessment of the compliance of the current state of a specialist's competence with all the required parameters for the entire time interval under consideration. To do this, we have to assume that each indicator will have its own worst perturbation (even if the same perturbation should take different values at the same time). At the same time, upon completion of monitoring, the program outputs the results in the form of a report, which indicates the time interval of observations of the actions of a particular crew member, records the facts of errors, and displays information about the degree of influence of the error on the final result (provided there are no corrective actions on the part of both the specialist and other crew members). The report ends with a two-point competent/incompetent rating system. The disadvantage of the program is its inability to indicate the degree of influence of external factors on the results obtained, but at the same time all the information contained in the report allows the expert who checks the competence of this specialist to conclude about the degree of safety of the actions taken by the employee in a particular situation. The results of the work of the guaranteeing program in the task of operating the GMSSB ship complex are given as illustrations.
guaranteed result method, competence assessment, management program, ship specialist, time space
Введение
На современном этапе развития морского образования в России для оценки качества профессиональной подготовки судовых специалистов применяются требования Международной конвенции о подготовке и дипломировании моряков и несении вахты 1978 г. (ПДМНВ-78) с поправками 2010 г. (Манильские поправки). Этот документ устанавливает минимальные стандарты компетентности специалистов различных судовых служб [1]. Понятие «компетентность» подразумевает систему сформированных знаний, умений, навыков специалиста в сфере его профессиональных обязанностей и способность их демонстрации на этапе его аттестации. При этом в ходе аттестации должна производиться проверка всех пунктов указанных стандартов (вместо принципа выборочной проверки, применяемой ранее). Нагрузка на экспертов, осуществляющих проверку компетентности (экзаменаторов), существенно возрастает – требуются большие затраты времени и одновременно детальное обоснование принятого решения (по каждому пункту стандарта) для достижения гарантированной объективности. В этой связи обеспечение качественной процедуры аттестации без использования специальных программных средств является крайне затруднительной задачей. С другой стороны, применение вычислительных средств для оценки компетентности также является непростым вопросом, т. к. тривиальный подсчет количества правильных и неправильных ответов в ходе выполнения испытуемым специалистом некоторого теста в лучшем случае (перечень вопросов и заданий полностью соответствуют стандарту компетентности, заложенные в вычислительную систему ответы не содержат ошибок, предусматривается возможность проверки ответов, не попадающих под «шаблонные» и т. д.) способен сформировать конечный результат – компетентен/некомпетентен с указанием процента правильных ответов. Все остальные параметры оценивания по-прежнему возлагаются на экзаменаторов (что является правильным), но достигаемая экономия времени оказывается незначительной. Поэтому более рациональным представляется разработка такого алгоритма оценивания, при котором вычислительная система оказывалась бы в состоянии констатировать не только правильность итогов выполнения подавляющего большинства зданий теста, но и проводить анализ действий испытуемого специалиста с точки зрения их эффективности. Такие алгоритмы будут являться оптимальными с точки зрения как сформированной итоговой оценки, так и степени объективности, а также будут обеспечивать рациональное распределение времени и нагрузки экзаменатора в ходе процедуры аттестации.
При выборе оптимальной оценки параметра компетенции судового специалиста в условиях неполной информированности можно рекомендовать к использованию, например, метод наилучшего гарантированного результата. Четкое определение этого метода дано в работе [2]. При этом реализация неопределенных субъективных факторов судового специалиста влияет только на критерий качества стороны процедуры оценки F(x, у). Иногда в процедуру оценки могут добавляться еще смешанные ограничения вида φ(x, у) > 0, выполнение которых обязательно для обеих сторон этой процедуры (процедура при наличии запрещенных ситуаций). В отличие от такого рода процедуры, ниже рассматриваются только несимметричные ситуации, а именно когда о соблюдении смешанных ограничений функции φ(x, у) > 0 должна заботиться сторона, выбирающая и оценивающая параметр х [3, 4].
Общая постановка задачи по выбору программы подготовки компетентного персонала
Пусть состояние компетенции субъекта – судового специалиста – оценивается векторами x Î X и y Î Y, определенными в подмножествах евклидовых пространств Еп и Ет, а φ(х, у) – вектор-функция: φ = (φ1, ..., φr). Кроме того, пусть множество X можно представить как пересечение всех множеств Х(у), определяющих допустимые значения х при различных значениях возмущения у Î Y:
![]() (1)
(1)
где
![]()
Тогда для каждой компоненты векторной функции φ можно выделить свое наихудшее возмущение, которое записывается следующим образом:
![]()
В интерпретации состояния компетенции судового специалиста выражения (1) справедливы для бесконечномерного случая, когда х и у – элементы функциональных пространств, например функции времени, F(x, у) – функционал, а множества Х(у) и Y задаются некоторыми операторами.
Для данной конкретной задачи оптимальной идентификации параметров состояния компетенции судового специалиста, содержащей возмущения ξ в правых частях дифференциальных уравнений, в начальных условиях и в смешанных ограничениях ψ на управление u и фазовые координаты х:
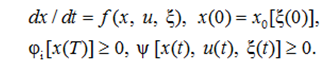
Требуется выбрать программу идентификации параметров состояния компетенции u(t)(0, T) на весь интервал времени (0, Т), зная только множество Ξ(t) возможных значений возмущений ξ(t) (функции f, х0, φ, ψ известны). При этом нужно гарантировать выполнение текущих (ψ ≥ 0) и конечных (φ ≥ 0) ограничений и максимизировать нижнюю оценку J* критерия качества J[х(T)], справедливую для любой реализации возмущения ξ(t) Î Ξ(t).
Чтобы сформировать гарантирующую программу идентификации параметров состояния компетенции, нужно решить серию вспомогательных вариационных задач, в которых искомыми параметрами будет наихудшее возмущение ξ, а программа u(t)(0, T) фиксирована [5, 6]. При этом психофизический фактор, наихудший для i-й компоненты конечных ограничений (i = l, ..., r), имеет вид:
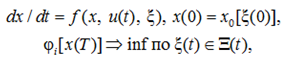 (2)
(2)
а психофизический фактор, наихудший для j-й компоненты текущих ограничений в момент t = τ(j = 1, ..., q, 0 ≤ τ ≤ T), может быть записан:
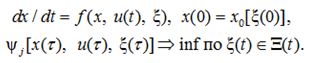 (3)
(3)
В то же время психофизический фактор, наихудший для критерия качества, может быть определен следующим образом:
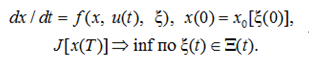 (4)
(4)
Для дальнейшего составления алгоритма оценивания компетенций испытуемого специалиста наихудшие психофизические факторы не требуются, нужны только зависимости минимальных значений функционалов задач (2)–(4) от программы u(t)(0, T) (они будут зависеть еще и от множества Ξ):
![]() при связях (2),
при связях (2),
![]() (5)
(5)
при связях (3),
![]() при связях (4).
при связях (4).
Искомая программа идентификации параметров компетенций судового специалиста и максимальная гарантированная оценка критерия качества такой программы могут быть определены из решения следующей задачи:
![]()
при
![]() (6)
(6)
![]()
При этом выражения (2)–(6) можно собрать в одну компактную запись:
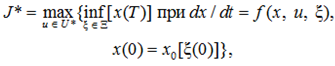 (7)
(7)
где U* определяется как множество всех идентифицирующих действий u, для которых выполняются неравенства
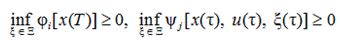 (8)
(8)
при
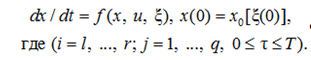
Далее, не затрагивая алгоритмической стороны вопроса, отметим, что полученные выражения (7) и (8) эквивалентны классической задаче
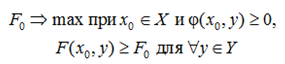 (9)
(9)
по сведению к максимину на независимых от реализаций y и x множествах X* и Y
![]() (10)
(10)
где множество X* сужено по сравнению с исходным множеством
![]() (11)
(11)
Для подтверждения эквивалентности задач (7), (8) и (9), (10) достаточно составить следующую схему: сначала установить совпадение множеств допустимых значений аргумента х в этих задачах, а затем – совпадение максимизируемых по аргументу х функций. Этого будет достаточно для подтверждения эквивалентности двух задач поиска экстремума [7, 8].
Для поставленной цели обозначим через X1 множество значений х, удовлетворяющих условиям задачи (11):
![]() (12)
(12)
Совпадение выражения (12) с множеством (11) в задаче (10) следует из определения точной нижней грани. Пусть х' Î Х1, но Í X*. Тогда infφ(x', y) < 0, т. е. найдется y'ÎY : φ(x', y') < 0, что означает x' Í X1. Полученное противоречие показывает, что из факта принадлежности x' Î X1 следует x' Î X* или X1 Í X*.
Пусть теперь x''Î X*, но Í X1. Тогда найдется y''ÎY : φ(x'', y'') < 0.
По определению имеем
то есть x" Í X*, что противоречит исходной посылке. Значит, из x" Î X* следует х" Î Х1, т. е. X1 Ê X*. Из сравнения с предыдущим заключаем: X1 = X*.
Покажем теперь, что существуют совпадения максимизируемых функций. Из определения точной нижней грани следует, что при любом фиксированном х
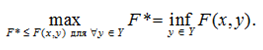 (13)
(13)
Действительно,
![]()
то есть последнее неравенство из выражения (9) выполняется. Если же попытаться увеличить F* по сравнению с (13), то это неравенство нарушится, т. к. по определению точной нижней грани для любого ε > 0 найдется такой у'(ε), что
![]()
Таким образом, равенство (13) подтверждено и оно означает, что и в выражении (9), и в выражении (10) максимизируется одна и та же функция от аргумента х.
Частная постановка задачи по выбору программы повышения уровня компетентности судового персонала
Проследим схему (7), (8) на задаче, допускающей аналитическое решение. Рассмотрим судового специалиста, функционирующего в условиях колебаний входного потока знаний и умений и выходного потока компетенции, относительно соответствующих требуемых значений, обеспечивающих безопасную эксплуатацию технических средств и судна в целом. Для заданного выходного потока компетенций требуется построить программу входного потока знаний и умений, зная только диапазоны будущих колебаний как потока знаний и умений, так и компетентности судового специалиста. Кроме того, в процессе составления программы потока знаний и умений (t < 0), поступающих к субъекту, не точно известны и те знания и умения, которыми будет обладать субъект к началу реализации этой программы (t = 0). Остальные детали поступления к субъекту знаний и умений представим в виде формализованной записи и списка обозначений:
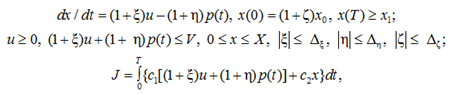 (14)
(14)
где х, х0, x1 и X – текущие, начальные, расчетные, конечные и максимальные количества знаний и умений, передаваемых судовому специалисту (x0, x1 и X заданы, при этом Х ≥ (1 + Δζ)x0, (1 – Δζ)x0 ≥ 0, X ≥ x1 ≥ 0); и и p(t) – плановые интенсивности входных знаний и умений, поступающих судовому специалисту, а также конвенционные характеристики этого специалиста (и – программа обучения, подлежащая выбору, как функция времени на заданном отрезке [0, T]; р(t) ≥ 0 – заданная на [0, Т] кусочно-непрерывная функция). Кроме того, задана величина V – максимальная скорость подачи знаний и умений судовому специалисту (задана); ζ – относительная ошибка в определении начального уровня подготовки специалиста; ξ и η – относительные колебания интенсивностей потока знаний и умений и относительные колебания компетентности судового специалиста (возмущения, неизвестные функции времени); Δξ, Δζ, Δη – границы колебаний интенсивностей потоков (заданы, 0 < Δξ, Δζ, Δη < 1).
Пусть далее J – суммарные затраты, идущие на подготовку специалиста и рассматриваемые как минимизирующий критерий качества подготовки специалиста, где заданные удельные затраты с1 и с2 на передачу знаний и умений и формирование компетентности специалиста. При таких допущениях вспомогательные вариационные задачи (2)–(4) являются линейными, а найденные в результате их решения наихудшие вариации величин ξ, ζ, η оказываются граничными и независящими от выбранной программы подготовки специалиста и(t):
– для ограничения интенсивности подачи знаний и умений:
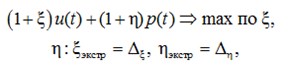 (15)
(15)
тогда должно быть
![]() ;
;
– для установки нижней границы оценки текущих знаний и умений:
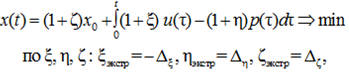 (16)
(16)
тогда должно быть
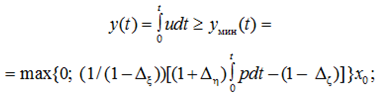
– для установки верхней границы оценки текущих знаний и умений:
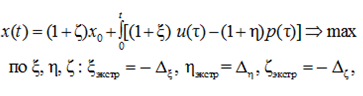 (17)
(17)
тогда должно быть
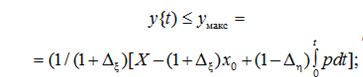
– для ограничения конечного запаса знаний и умений:
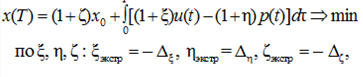 (18)
(18)
тогда должно быть
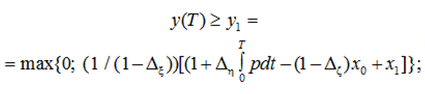
– для критерия качества:
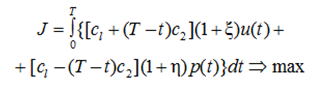 (19)
(19)
согласно
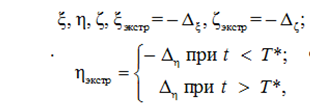
где (Т* = max{0; T – c1c2}), и тогда должно быть
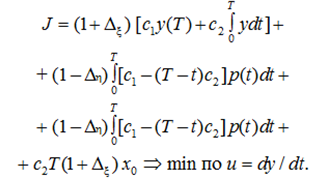
Таким образом, наихудшие вариации компетенции для различных контролируемых характеристик получились различными. Каждая из них имеет простой физический смысл, быть может, за исключением ηэкстр из выражения (19). Вариация в потоке знаний и умений η, наихудшая для критерия, переключается в момент t = T* с нижней границы на верхнюю границу. Это объясняется тем, что величина η по-разному влияет на разные слагаемые критерия. Увеличение интенсивности потока знаний и умений увеличивает расходы на идентификационные расходы, но зато уменьшает расходы на сохранение состояния компетентности судового специалиста, поскольку текущее состояние компетенции при увеличении η падает [9, 10].
Второй эффект – интегральный, он оказывается преобладающим на длинных траекториях (T >> c1 / c2), на которых большую часть времени вариация компетентности специалиста направлена на увеличение (η = –Δη – магистральный режим). В конце, на интервале постоянной протяженности (c1 / c2), состояние компетентности переключается на увеличение интенсивности потока знаний и умений (η = Δη), а на коротких траекториях (T’ ≤ c1 / c2) магистральный режим отсутствует.
Сведя воедино все ограничения из (15)–(18) и выделив в (19) из последнего выражения для критерия члены, зависящие от процедуры идентификации и (первые квадратные скобки), получим следующую вариационную задачу для определения наилучшей гарантирующей процедуры по идентификации состояния компетентности судового специалиста u(t) = dy(t) / dt:
 (20)
(20)
Здесь уместно напомнить что у1, uмакс(t), yмин(t), yмакс(t) заданы соотношениями (15)–(18), при этом у1 ≥ yмин(T), а yмин(t) и yмакс(t) – неубывающие функции времени с единственной точкой пересечения t**: yмин(t) < yмакс(t), когда t > t**. Новая переменная y(t), определенная в выражении (16), означает суммарный поток знаний и умений, поступающих судовому специалисту за период [0, t]. Это непрерывная кусочно-дифференцируемая функция времени, подлежащая выбору.
Программа поставок специалисту знаний и умений вычисляется как ее производная u(t) = dy(t) / dt.
Очевидно, что для существования решения задачи (20) необходимо
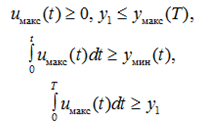 (21)
(21)
(из второго условия (21) следует, что t** > T).
Структура функционала I такова, что если существует допустимая по условиям (20) кривая у*(t), ограничивающая снизу все допустимые у(t), то она и будет решением задачи (20). Такую кривую можно строить с конца, от t = T:
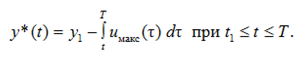 (22)
(22)
Этот участок с максимальной производной продолжается до ближайшего к Т момента t1 пересечения с yмин(t) (такой всегда существует в силу последнего условия из (21)):
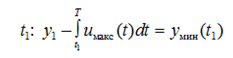 (23)
(23)
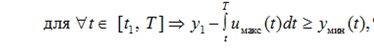
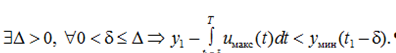
В предельном случае, когда y1 = yмин(T) и для некоторой окрестности Т
![]()
участок (22) вырождается в точку (t1 = T). Участок (22) сменяется участком движения у по своей нижней границе
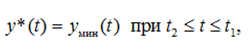 (24)
(24)
которое продолжается, пока наклон границы не превысит соответствующего предела uмакс(t):
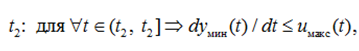 (25)
(25)
![]()
Если смены знака первого неравенства в (25) не происходит, то участок (24) сохраняется до t = 0 (например, когда yмин(t1) = 0). В противном случае слева от t2 опять нужно расположить участок типа (22), затем (24) и т. д. Заканчивается построение участком типа (24), когда он охватит момент t = 0 (это обязательно произойдет в силу предпоследнего условия (21)). В результате траекторию у*(t) можно представить так:
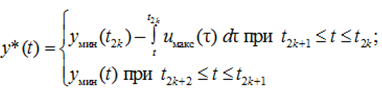 (26)
(26)
![]()
где моменты переключений t2k определяются соотношениями (25) (в которых надо заменить t2 на t2k, t1 на t2k – 1), а моменты t2k + 1 – соотношениями (23) (в которых надо заменить y1 на величину умин(t2k), t1 на t2k + 1, а Т на t2k).
Далее покажем, что траектория (26) ограничивает снизу все допустимые траектории. Предположим противное, т. е. что существует некоторая допустимая траектория y~(t) и хотя бы один момент времени t' Î (0, Т), где y~(t') < y*(t'). На участках [t2k + 2, t2k + 1] это произойти не может, поскольку тогда окажется y~(t') < yмин(t'), что противоречит предположению о допустимости y~(t). Если же t' Î (t2k + l, t2k), то у~(t) пересечется с yмин(t') раньше, чем у*(t), когда еще нет возможности двигаться по нижней границе из-за невыполнения условия dy(t) / dt ≤ uмакс(t) (25). Снова получается противоречие с предположением о допустимости у~(t).
Таким образом, все допустимые траектории y(t) ≥ y*(t) для всех t Î [0, Т], отсюда
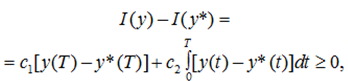
что означает оптимальность траектории (26), если она допустима.
В процессе построения траектории y*(t) удовлетворялись все условия из второй строчки (20), кроме последнего: y(t) ≤ yмакс(t). Но ни одна допустимая траектория не опускается ниже у*(t), поэтому остается только проверить выполнение этого ограничения сверху для построенной траектории. Если окажется, что y*(t) ≤ yмакс(t) для всех t Î [0, Т], то решение задачи (20) найдено, в противном случае решения не существует. В совокупности с условиями (21) данное условие образует систему необходимых и достаточных условий существования решения. Если исходные данные задачи (20) не удовлетворяют этой системе, то гарантированного поддержания состояния компетенции судового специалиста в классе программ (без использования дополнительных сведений о текущих вариациях психофизических факторов) построить невозможно.
Траектория (26) получилась не зависящей от коэффициентов c1 и с2 в функционале, т. е. от стоимости используемых знаний и умений и от стоимости их хранения на судах или в учебных центрах (от них зависит только значение функционала). При нулевой стоимости хранения знаний и умений (с2 = 0) наряду с траекторией (26) оптимальной будет любая допустимая (по ограничениям (20)) траектория, для которой у(Т) = у1. Это объясняется тем, что в данном случае безразлично, к какому моменту накапливать необходимое количество знаний и умений, в то время как при с2 > 0 выгодно это делать как можно более поздно. Отметим еще, что у*(t) = 0 при y1 = 0.
Уравнения (14)–(26) позволяют относительно несложно составить алгоритм объективной оценки компетентности судового специалиста при наличии средств наблюдения за его действиями в ходе процедуры аттестации. В качестве примера рассмотрим отчет, сформированный экзаменационной программой, сравнивающей действия испытываемого специалиста в тренажере Transas GMDSS Simulator 5000 v.8.50.113412 с действиями, которые заранее были предложены в качестве оптимальных экспертами в области судовой радиосвязи. Удобство выбранного тренажера заключается в том, что при его использовании автоматически формируется текстовый журнал с действиями слушателя, которые легко можно сравнить с оптимальным «шаблоном».
В рассматриваемом примере в качестве одной из экзаменационных задач был предложен следующий сценарий: судно Arcona, совершающее переход из порта Хаммерфест в порт Киркенес, получает сигнал бедствия от судна Canadian Star, находящегося в координатах 70°55' с.ш., 25°35' в.д., в 20 морских милях от него. При этом предполагалось, что судно Canadian Star получило пробоину ниже ватерлинии в условиях сильного волнения, экипаж покинул судно, передав сигнал бедствия с использованием устройства цифрового избирательного вызова (ЦИВ) диапазона ультракоротких волн (УКВ) в коротком формате (без указания характера бедствия), а приемник GPS, подключенный к УКВ ЦИВ, получил повреждение и включил в переданный сигнал устаревшие координаты (70°35' с.ш., 25°30' в.д.), экипаж может продержаться до подхода помощи не более 1,5 ч.
В таблице представлен краткий отчет, сформированный экзаменационной программой по результатам сравнения действий слушателя в указанной ситуации с оптимальным вариантом.
Сравнительный анализ действий испытуемого лица при выполнении экзаменационного задания
Comparative analysis of the actions of the tested person when performing the examination task
|
Время |
Этап сценария |
Действия |
Оптимальный |
Оценка потерь времени и допущенного слушателем риска |
|
07.12 UTC |
Судно Canadian Star передало сигнал бедствия: nature: undesignated pos: 70°35N 025°30E time: 05.30 UTC |
Изменение курса судна и следование полным ходом (20 уз) к точке, обозначенной как место бедствия |
Переключение УКВ радиостанции на |
Установление соединения с оператором береговой радиостанции – 5 мин; следование к неверной точке, принятой за место бедствия, – 5 мин; допущенный риск – |
|
07.22 UTC |
Судно Arcona начало движение в сторону истинного положения судна Canadian Star |
Движение средним ходом по наикратчайшему пути следования, поддержание радиосвязи с оператором береговой радиостанции в диапазоне УКВ |
Движение полным ходом по дуге с огибанием фьордов, поддержание радиосвязи с оператором береговой радиостанции в диапазоне промежуточных волн |
Движение средним ходом с маневрированием допущенный риск – |
|
08.30 UTC |
Судно Arcona прибыло в район бедствия судна Canadian Star
|
Установление радиосвязи с экипажем судна, терпящего бедствия, для получения дополнительной информации, определение местоположения людей, покинувших судно Canadian Star,
|
Определение местоположения людей, покинувших судно Canadian Star, с использованием радиолокационной станции и радиопеленгатора, установление радиосвязи с экипажем судна, терпящего бедствия, для получения дополнительной информации |
Первоначальная попытка установления радиосвязи с экипажем судна, терпящего бедствия, 4 мин – на определение истинного местоположения терпящих бедствие людей; допущенный риск – |
|
Итоговый результат |
Суммарная потеря времени – 44 мин. Суммарный допущенный риск – 8 баллов (максимально возможный риск – 15 баллов). Оценка – компетентен (конечная цель задания выполнена успешно), степень влияния допущенных ошибок – значительная по времени (итоговый запас – 12 мин), выше среднего с точки зрения допущенного риска (53,3 % от максимально допустимого) |
|||
Согласно представленным в таблице данным программа в рассматриваемой ситуации производит оценку по трем параметрам – правильность выполняемых действий с аппаратурой Глобальной морской системы связи при бедствии (ГМССБ) и управления судном, допущенная потеря времени (по сравнению с оптимальным вариантом действий), допущенный риск по 5-балльной системе (0 – последовательность предпринятых действий абсолютно безопасна, 5 – последовательность предпринятых действий неминуемо приведет к провалу всего задания). Таким образом, предложенный алгоритм экзаменационного оценивания способен обеспечить гарантированную оценку компетентности судового специалиста (итоговый результат + детальное обоснование принятого решения). Следует отметить, что для достижения такого результата в программе требуется предусмотреть детальную декомпозицию действий слушателя, принимаемых за оптимальный вариант, что возможно только в случае применения тренажеров, формирующих достаточно подробный отчет действий слушателя в ходе его использования. Тогда роль экзаменатора сводится к анализу степени влияния внешних факторов на достигаемый результат, не учитываемых программой (экзаменационный алгоритм производит оценку для наихудшего возможного варианта, судовой специалист полагается абсолютно устойчивым к воздействию различного рода психоэмоциональных воздействий – плохое самочувствие, наличие стрессовой обстановки и т. д.). Конечное решение эксперта сводится к принятию решения – провести дополнительную проверку специалиста с использованием нового экзаменационного задания (если роль внешних факторов признана экспертом как существенно значимая), в остальных случаях оставить оценку, поставленную экзаменационной программой без изменения.
Заключение
Применение принципа наилучшего гарантированного результата в задачах программного управления, в случае когда возмущение действует сразу на несколько контролируемых показателей (текущие ограничения, конечные условия, критерий качества), является достаточно эффективным.
Так, при выборе программы управления, когда реализация возмущения неизвестна, а известно только множество возможных реализаций, программа управления, построенная на гарантирующем принципе, на всем рассматриваемом интервале времени возможна лишь при условии, что на каждый показатель будет действовать свое наихудшее возмущение (даже если при этом одно и то же по наименованию возмущение должно одновременно принимать разные значения).
1. Mezhdunarodnaia konventsiia o podgotovke i diplomirovanii moriakov i nesenii vakhty 1978 goda (PDMNV-78) s popravkami (konsolidirovannyi tekst) [International Convention on Training, Certification and Watchkeeping of Seafarers, 1978 (STCW-78) as amended (consolidated text)]. Saint-Petersburg, TsNIIMF, 2016. 823 p.
2. Kosorukov O. A., Khalikov M. A., Fomin G. P. Modeli issledovaniia operatsii [Research models of operations]. Moscow, Rusains Publ., 2019. 190 p.
3. Germeier Iu. B., Vatel' I. A. Igry s ierarkhicheskim vektorom interesov [Games with hierarchical vector of interests]. Tekhnicheskaia kibernetika, 1974, no. 3, pp. 54-69.
4. Men'shikov V. I., Pasechnikov M. A., Pen'kovskaia K. V., Pen'kovskii D. V. Osobennosti ekspluatatsii sudov kompaniiami s integrirovannoi sistemoi menedzhmenta [Features of ship operation by companies with integrated management system]. Murmansk, Izd-vo MGTU, 2014. 195 p.
5. Gritsova O. A., Nosyreva A. N., Mikhailova O. M. Primenenie teorii igr v upravlenii personalom [Application of game theory in personnel management]. Regional'nye problemy preobrazovaniia ekonomiki, 2019, no. 10, pp. 263-268.
6. Raifa G. Analiz reshenii [Analysis of solutions]. Moscow, Nauka Publ., 1977. 287 p.
7. Vediakova A. O., Milovanovich E. V., Slita O. V., Tertychnyi-Dauri V. Iu. Metod teorii optimal'nogo upravleniia [Method of optimal control theory]. Saint-Petersburg, Izd-vo Un-ta ITMO, 2021. 219 p.
8. Khazen E. M. Metody optimal'nykh statisticheskikh reshenii i zadachi optimal'nogo upravleniia [Methods of optimal statistical solutions and optimal control problems]. Moscow, Sovetskoe radio Publ., 1968. 467 p.
9. Feinstein A. Foundations of information theory. New York, McGraw-Hill, 1958. 137 p. (Russ. ed.: Fainstein A. Osnovy teorii informatsii / per. s angl. I. N. Kovalenko i E. R. Nitskoi. M.: Izd-vo inostrannoi literatury, 1960. 140 s.).
10. Feller W. An Introduction to Probability Theory and Its Applications, Volume 2. Wiley, 1966. 704 p. (Russ. ed.: Feller V. Vvedenie v teoriiu veroiatnostei i ee prilozheniia: v 2 t. / per. s angl. Iu. V. Prokhorova. M.: Mir, 1984. T. 2. 751 s.).

















