Power Machines - ZTL, LMZ, Electrosila, Energomachexport, JSC (Leading Design Engineer; the Department of General Industrial Electric Drive)
Russian Federation
Russian Federation
The article considers the mathematical description and comparison of the most common methods of pulse-width modulation (PWM) for a three-phase voltage inverter, namely vector PWM, PWM with third harmonic premodulation and classical PWM. In contrast to the classical mathematical description of PWM, a description is presented that is close to the implementation of modulation using modern microcontroller technology. The classic representation of PWM is based on comparing two signals. In this representation, the modulation pulse occurs at the moment when the modulating function is greater in value than the reference signal. When implementing PWM by a microcontroller, the pulse is placed within the period symmetrically with respect to the middle of the interval, while the pulse width is determined by the average value of the voltage modulating function. With a different mathematical description of PWM, the pulse is located differently within the modulation interval. There are presented the results of modeling and compares the mathematical descriptions of PWM methods according to the criterion of minimum dispersion of the current flowing in the load. As a result of the comparison, it was revealed that the same, differently described PWM algorithm gives different results. A comparison of vector PWM with a modified vector PWM was made. The modification consists in applying a dynamic pulse shift algorithm in such a way as to obtain a minimum of current dispersion in the load. Comparison of PWM methods was carried out at different frequencies of the reference signal; a static RL circuit was used as a load when simulating a three-phase voltage inverter. The results obtained allow us to recommend a pulse shift algorithm for implementing PWM in voltage inverters operating at relatively low PWM frequencies. Minimization of the current dispersion makes it possible to obtain improved energy and vibration-noise characteristics of the electric drive.
pulse-width modulation, vector PWM, classical PWM, premodulation, induction motor, current quality, current dispersion
Введение
Освоение Северного морского пути невозможно без мощных кораблей-ледоколов. В системах электродвижения такого рода судов эксплуатируются мощные гребные электродвигатели переменного тока. Мощность таких двигателей может достигать десятки мегаватт. Например, на ледоколе «Арктика» эксплуатируются шесть электродвигателей суммарной мощностью 60 МВт. Электропитание двигателей в подобных системах осуществляется от мощных электрических преобразователей. Для формирования выходного напряжения этих преобразователей применяется широтно-импульсная модуляция (ШИМ), процесс модуляции с фиксированной частотой и меняющейся шириной импульсов. При этом из-за ограничения по потерям, которые выделяются на ключах преобразователя, частота ШИМ может иметь относительно низкие значения и находиться в пределах диапазона 500–1 000 Гц. Импульсная форма выходного напряжения инвертора порождает в нагрузке ток с гармоническими искажениями. Гармонические искажения вызывают дополнительные потери в электродвигателе и ухудшают виброакустические характеристики электропривода. В отечественной и иностранной литературе много внимания уделено сравнению методов ШИМ [1–3]. Настоящая статья посвящена математическому описанию ШИМ и его сравнению, а также сравнению методов ШИМ по критерию минимума дисперсии тока в нагрузке.
Наибольшую известность и распространение получили следующие виды ШИМ:
– синусоидальная ШИМ [4, 5];
– ШИМ с предмодуляцией третьей гармоникой [6, 7];
– векторная ШИМ [8].
Методы и материалы исследования
Классическое представление ШИМ.
Обычно в классическом (аналоговом) описании процесса формирования импульсов ШИМ используют два сигнала (две функции), которые сравнивают между собой: опорный сигнал и модулирующую функцию. Наиболее распространенная форма опорного сигнала – центрально-симметричная пила. Модулирующая функция может принимать различные формы, различным формам модулирующих функций соответствуют различные виды ШИМ [9].
Коммутационная функция, определяющая состояние ключей полумоста, имеет следующий вид:
χх = θ(γх – φ(t)),
где θ – единичная функция; γх – моделирующая функция потенциала полумоста; φ(t) – опорный сигнал.
Модулирующая функция потенциала полумоста определяется следующей формулой:
γх = gx + γ0 – ψ0,
где gx – модулирующая функция фазного напряжения; γ0 = 1/2 – нулевая потенциальная функция; ψ0 – функция предмодуляции.
При описании синусоидальной ШИМ полагается, что функция предмодуляции ψ0 равняется нулю, т. е. потенциал нулевой точки нагрузки принимается равным Ud / 2. Модулирующие функции потенциалов полумостов при синусоидальной ШИМ представлены на рис. 1.

Рис. 1. Вид модулирующих функций потенциалов полумостов при синусоидальной ШИМ
Fig. 1. Type of modulating functions of half-bridge potentials at sinusoidal PWM
При описании ШИМ с предмодуляцией полагается, что функция предмодуляции ψ0 имеет частоту третьей гармоники и амплитуду, равную 1/4 (могут приниматься и другие значения амплитуды [6, 7]) от амплитуды модулирующей функции фазного напряжения. В этом случае полагается, что потенциал нулевой точки нагрузки будет меняться по гармоническому закону с постоянной составляющей, равной γ0. Модулирующие функции потенциалов полумостов и нулевой точки нагрузки при ШИМ с предмодуляцией представлены на рис. 2.
Для описания процесса формирования импульсов при векторной ШИМ обычно используется набор векторов. Эти векторы разделяются на активные и нулевые. Каждому вектору соответствует определенное состояние ключей инвертора.
Формирование импульсов при векторной ШИМ также может быть описано с помощью сравнения модулирующей функции и опорного сигнала [10]. При векторной ШИМ функция предмодуляции ψ0 определяется следующей формулой:
ψ0 = (max(gx) + min(gx)) / 2.
При таком описании полагается, что потенциал нулевой точки нагрузки будет меняться по закону, близкому к треугольному, с постоянной составляющей, равной γ0. Модулирующие функции потенциалов полумостов и нулевой точки нагрузки при векторной ШИМ представлены на рис. 3.
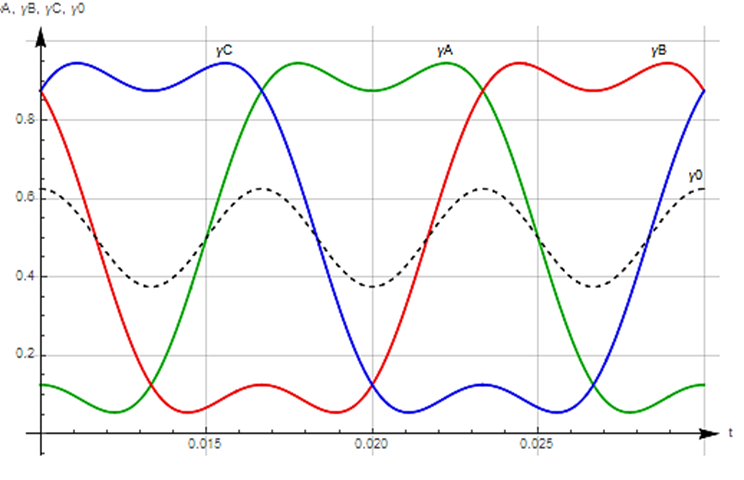
Рис. 2. Моделирующие функции потенциалов полумостов при ШИМ с предмодуляцией
Fig. 2. Modeling functions of potentials of half-bridges at PWM with premodulation

Рис. 3. Моделирующие функции потенциалов полумостов при векторной ШИМ
Fig. 3. Modeling functions of half-bridge potentials at vector PWM
На рис. 4 представлен процесс формирования коммутационной функции (процесс модуляции) для синусоидальной ШИМ. Значениям коммутационной функции, равной единице, соответствует открытое состояние верхнего ключа и закрытое состояние нижнего ключа полумоста. При значении коммутационной функции, равной нулю, ключи полумоста меняют свои состояния на противоположные.

Рис. 4. Коммутационная функция полумоста при классической ШИМ
Fig. 4. Switching function of a half-bridge at classical PWM
Для других видов ШИМ, рассматриваемых в статье, процесс модуляции выглядит аналогично, поэтому дополнительные графики не представлены.
Описание ШИМ, формирующееся микроконтроллером.
В современном электроприводе ШИМ реализуется с использованием электроники, а именно микроконтроллеров. При этом сформированный импульс ШИМ будет размещается симметрично относительно центра интервала модуляции. Данный факт вносит корректировку в математическое описание процесса формирования импульсов ШИМ, т. к. при классическом описании ШИМ местоположение импульса внутри периода модуляции определяется естественным образом при сравнении. Для имитации опорного сигнала – симметричной пилы в микроконтроллере – используется счетчик (цифровая пила). Для сравнения с счетчиком используется не модулирующая функция сигнала, а среднее значение модулирующей функции на периоде ШИМ. Именно среднее значение модулирующей функции за период ШИМ сравнивается с нарастающим и спадающим фронтом цифровой пилы, в результате чего импульс располагается симметрично относительно интервала модуляции. На рис. 5 представлены импульсы классической ШИМ при ее реализации микроконтроллером.
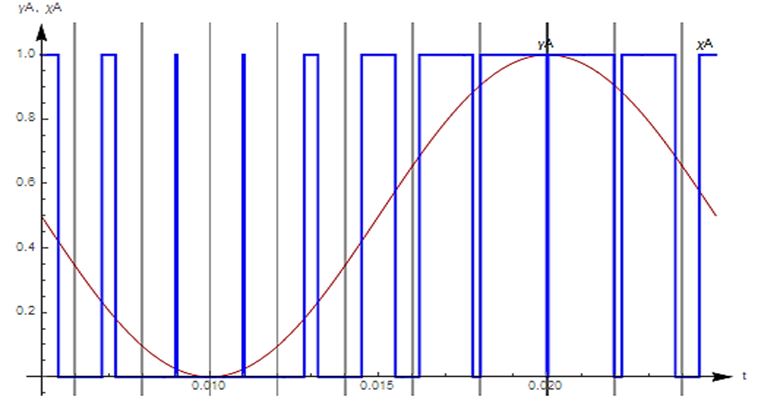
Рис. 5. Расположение импульсов ШИМ при ее реализации микроконтроллером
Fig. 5. Location of PWM pulses when implemented by a microcontroller
Для других видов ШИМ, рассматриваемых в статье, процесс модуляции, реализованный с помощью микроконтроллера, выглядит аналогично.
Дисперсия тока.
Как отмечалось в Введении, импульсная форма выходного напряжения преобразователя порождает в нагрузке ток с гармоническими искажениями. Для оценки качества тока в нагрузке в статье применяется дисперсия тока:

где j(ϕ) – желаемый ток, порождаемый модулирующей функцией; i(ϕ) – ток, полученный в результате модуляции.
При моделировании описанных выше методов ШИМ применялись и сравнивались два вида представления ШИМ: классический (аналоговый) и микроконтроллерный. Результаты моделирования представлены в табл. 1. При моделировании в качестве нагрузки трехфазного инвертора напряжения использовалась статическая RL-цепь, параметры моделирования также приведены в табл. 1.
Таблица 1
Table 1
Результаты моделирования наиболее распространенных видов ШИМ при различных видах описания
Simulation results of the most common types of PWM when describing various types
|
Вид описания |
Синусоидальная ШИМ |
ШИМ с предмодуляцией |
Векторная ШИМ |
|
fg = 50 Гц; fШИМ = 1 000 Гц; R = 1 Ом; L = 0,01 Гн; Ud = 1 В |
|||
|
Классический |
7,48‧10–6 |
5,13‧10–6 |
6,65‧10–6 |
|
Микроконтроллерный |
7,66‧10–6 |
5,23‧10–6 |
5,29‧10–6 |
Согласно табл. 1 один и тот же метод ШИМ, описанный двумя разными способами, дает отличающиеся друг от друга результаты. В первую очередь это достигается за счет различного положения импульса внутри интервала ШИМ. Из этого следует, что качество тока напрямую зависит от положения импульса внутри периода ШИМ.
В работах [6, 7] найдена зависимость дисперсии тока от положения импульса и определено оптимальное положение импульса ШИМ внутри периода модуляции по критерию минимума дисперсии тока в нагрузке. Сдвиг импульса относительно центра интервала модуляции определяется формулой
Δα = (11 / 96)ΔgxTШИМ, (1)
где Δgx – относительное приращение моделирующей функции на интервале ШИМ.
Назовем данный алгоритм ШИМ модифицированной микроконтроллерной ШИМ.
В соответствии с формулой (1) отметим, что чем меньше значения периода ШИМ, тем меньше приращение моделирующей функции Δgx. При малых значениях периода ШИМ импульс стремится занять место симметрично в середине интервала модуляции. Поэтому данный алгоритм разумно использовать при низких значениях относительной частоты ШИМ. Под относительной частотой ШИМ понимается отношение периода опорного сигнала к периоду модулирующей функции.
Векторная ШИМ несложно реализуется с помощью современных микроконтроллеров и имеет коэффициент использования напряжения источника питания, равный 1, поэтому произведем моделирование и сравнение векторной микроконтроллерной ШИМ с векторной модифицированной (оптимальной по критерию минимума дисперсии тока) микроконтроллерной ШИМ. Моделирование произведено на разных частотах ШИМ, результаты и параметры моделирования представлены в табл. 2. Графики токов, полученных в результате моделирования на частоте 500 Гц, представлены на рис. 6.
Таблица 2
Table 2
Результаты моделирования векторных ШИМ*
Vector PWM simulation results
|
fШИМ, Гц |
Векторная микроконтроллерная ШИМ D |
Векторная модифицированная |
|
fg = 50 Гц; R = 1 Ом; L = 0,01 Гн; Ud = 1 В |
||
|
500 |
1,27 |
1,0 |
|
1 000 |
1,08 |
1,0 |
|
1 500 |
1,03 |
1,0 |
*Выделенной курсивом единице соответствует минимальное значение дисперсии, цифре без выделения – значение дисперсии, приведенное к минимальному.
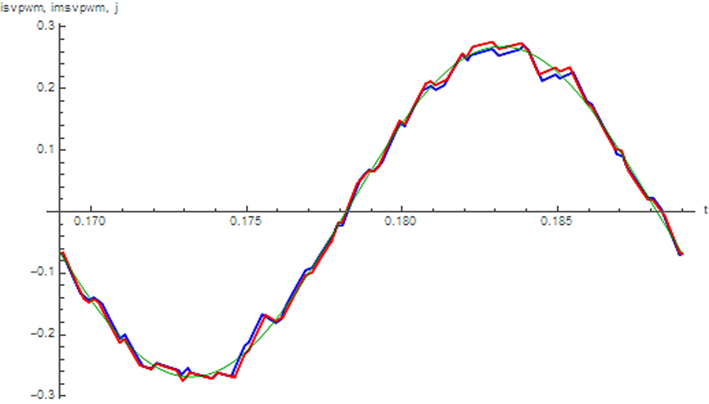
Рис. 6. Графики токов: 1 – желанный ток; 2 – ток при модифицированной векторной ШИМ;
3 – ток при векторной ШИМ
Fig. 6. Graphs of currents: 1 - desired current; 2 - current at modified vector PWM; 3 - current at vector PWM
Результаты, занесенные в табл. 2, подтверждают работоспособность алгоритма сдвига импульса модифицированной ШИМ.
Заключение
Поскольку в настоящее время при формировании ШИМ используется современная микроэлектроника и при ШИМ, сформированной с помощью микроконтроллера, импульс помещается симметрично относительно центра интервала ШИМ, то классическое математическое описание ШИМ является некорректным. Более точным является математическое описание, в котором импульс помещается симметрично относительно центра интервала модуляции, т. к. это происходит при реализации микроконтроллером.
При синтезе ШИМ для мощных инверторов, работающих на относительно низких частотах модуляции, целесообразно применять ШИМ с алгоритмом динамического сдвига импульса внутри периода. Алгоритм сдвига импульса позволяет улучшить качество тока, протекающего в нагрузке. Повышение качества тока влечет за собой уменьшение виброакустического шума, уменьшение пульсации электромагнитного момента двигателя, а также уменьшение потерь и, как следствие, повышение энергоэффективности привода. Также данный алгоритм может применяться при синтезе ШИМ активным выпрямителем, это позволит отдавать в сеть ток более высокого качества [11, 12].
При значениях относительных частот ШИМ более 30 алгоритм динамического сдвига импульса не дает ощутимого эффекта, т. к. при больших частотах ШИМ приращение модулирующей функции мало, при этом импульс самостоятельно стремится в центр интервала модуляции.
Алгоритм ШИМ с динамическим сдвигом импульса может применяться в скалярных и векторных системах управления электропривода переменного тока.
1. Obukhov S. G., Chaplygin E. E., Kondrat'ev D. E. Shirotno-impul'snaia moduliatsiia v trekhfaznykh invertorakh napriazheniia [Pulse-width modulation in three-phase voltage inverters]. Elektrichestvo, 2008, no. 8, pp. 23-31.
2. Çetin N. O., Hava A. M. Scalar PWM implementation methods for three-phase threewire inverters. Electrical and Electronics Engineering. ELECO 2009. International Conference on Publication Year, 2009. Pp. 447-451.
3. Garces L. J. Current control of field oriented AC induction motor drives. An IEEE Tutorial: Microprocessor Control of Motor Drives and Power Converters. Canada, Toronto, 1993. Pp. 5-46.
4. Hava A. M., Kerkman R. J., Lipo T. A. A High Performance Generalized Discontinuous PWM Algorithm. IEEE Applied Power Electronics Conference, Atlanta, Georgia. February 1997. Vol. 2. Pp. 886-891.
5. Holmes D. G., Lipo T. A. Pulse width modulation for power converters: Principles and Practice. New-York, Wiley-IEEE Press, 2003. 734 p.
6. Bakhovtsev I. A., Zinov'ev G. S. Obobshchennyi analiz vykhodnoi energii mnogofaznykh mnogourovnevykh invertorov napriazheniia s shirotno-impul'snoi moduliatsiei [Generalized analysis of output energy of multi-phase multi-level voltage inverters with pulse-width modulation]. Elektrichestvo, 2016, no. 4, pp. 26-33.
7. Hava A. M., Çetin N. O. A Generalized Scalar PWM Approach with Easy Implementation Features for Three-Phase, Three-Wire Voltage-Source Inverters. IEEE Transactions on Power Electronics, 2011, vol. 26, no. 5, pp. 1385-1395.
8. King. K. G. A three phase transistor class-b inverter with sinewave output and high efficiency. Institute of Electrical Engineers Conference Published 123. 1974. Pp. 204-209.
9. Belousov I. V., Gel'ver F. A., Samoseiko V. F., Khomiak V. A. Shirotno-impul'snye preobrazovateli elektricheskoi energii: monografiia [Pulse-width converters of electrical energy: monograph]. Saint-Petersburg, Krylovskii gosudarstvennyi nauchnyi tsentr Publ., 2019. 231 p.
10. Belousov I. V., Samoseiko V. F., Brovtsinova L. M. Sravnitel'nyi analiz metodov shirotno-impul'snoi moduliatsii [Comparative analysis of pulse-width modulation methods]. Vestnik Gosudarstvennogo universiteta morskogo i rechnogo flota imeni admirala S. O. Makarova, 2018, vol. 10, no. 2, pp. 420-429.
11. Samoseiko V. F., Belousov I. V., Gel'ver F. A., Khomiak V. A. Algoritmy upravleniia elektricheskimi mashinami: monografiia. Vol. 1. Algoritmy upravleniia asinkhronnoi elektricheskoi mashinoi [Control algorithms for electrical machines: monograph. Vol. 1. Control algorithms for an asynchronous electrical machine]. Saint-Petersburg, Krylovskii gosudarstvennyi nauchnyi tsentr Publ., 2020. 116 p.
12. Samoseiko V. F. Teoreticheskie osnovy upravleniia elektroprivodom [Theoretical foundations of electric drive control]. Saint-Petersburg, Elmor Publ., 2007. 464 p.

















