Samara, Russian Federation
The paper considers an approach for solving the joint optimization problem of design solutions and modes of inductor functioning in the process of heating steel parts of L-shaped form for surface hardening. The first stage solves the problem of optimizing the design of the coils of the inductor and the parameters of the power supply control algorithm, ensuring the maximum uniform heating of the quenched layer to a given temperature above the Curie point in a fixed time. In the second step, a phase limitation is considered, which is a technological requirement to ensure, throughout the heating stage, a temperature not exceeding the limit value. In case of violation of the specified limit, the problem of finding the control algorithm on a special interval within which the maximum temperature in the hardened layer exceeded the maximum permissible value is solved. In the third step, the problem of joint optimization is solved with the found control algorithm at a specific interval of motion on the phase restriction. The described steps can be repeated if necessary. There is presented a test example of the application of the developed strategy for the considered class of technology induction heating for the surface hardening of metal blanks with an angle zone. For the numerical solution in the MATLAB application package developed a software complex, in which integrated two-dimensional nonlinear problem-oriented model of the induction heating process, developed in ANSYS Mechanical APDL. The algorithm for solving the joint optimization problem is based on an alternate method of parametric optimization of systems with distributed parameters. Developed strategy tested on a verified model of interconnected electromagnetic and temperature fields, it is possible to obtain a uniform temperature distribution along the boundary of the hardened layer of steel semi-finished products of complex geometric shape without local overheating throughout the heating stage.
induction heating, surface hardening, joint optimization, control algorithm, phase limitation, ANSYS
Введение
В машиностроительном производстве одной из ключевых задач является повышение надежности и увеличения срока службы ответственных деталей. Для этого стальные втулки, специальные подпятники, валы, шестерни и другие металлические полуфабрикаты сложной геометрической формы проходят широко распространенную процедуру термообработки – поверхностную закалку, основная цель которой – обеспечение достаточной твердости поверхностного слоя детали в сочетании с необходимой упругостью ее сердцевины. В настоящее время процесс закалки на практике часто реализуют в комплексных установках, представляющих собой скоростной индукционный нагреватель и высокоинтенсивный спрейерный охладитель. Качество процесса закалки во многом достигается за счет равномерного температурного распределения в поверхностном слое в конце стадии нагрева, который особенно сложно обеспечить в угловых зонах заготовок.
В этой связи особую важность приобретает возможность оптимизации конструктивных параметров нагревателя и режимов нагрева путем управления током индуктора. Математическое моделирование процесса нагрева стальных заготовок с угловыми зонами подробно описано в работах [1–4]. Статья посвящена разработке стратегии и численному решению совместной задачи оптимального проектирования и управления стадией нагрева процесса поверхностной индукционной закалки деталей сложной геометрической формы.
Численное моделирование стадии нагрева
Для исследования процессов индукционного нагрева под поверхностную закалку деталей с угловыми зонами в пакете прикладных программ (ППП) ANSYS Mechanical APDL разработана двумерная численная осесимметричная модель системы «индуктор – заготовка», реализующая расчет взаимосвязанных электромагнитной и тепловой задач [1, 2, 5, 6]. Оценка влияния конструкции витков и режима работы индукционного нагревателя на распределение температуры в поверхностном слое угловой зоны проведена на примере нагрева ступенчатой втулки или аналогичной L-образной заготовки из типовой углеродистой стали 40 (SAE 1040) [7]. Исходные данные для моделирования стадии нагрева представлены в табл. 1.
Таблица 1
Table 1
Исходные данные для моделирования стадии нагрева
Input data for heating stage simulation
|
Параметр |
Значение |
|
Начальная температура заготовки Ta, °С |
20 |
|
Длительность стадии индукционного нагрева τ°, с |
10 |
|
Требуемая температура вдоль границы закаливаемого слоя Tdes, °С |
900 |
|
Высота заготовки H, мм |
50 |
|
Длина границы закаливаемого слоя ABCDEF стальной заготовки L, мм |
≈ 55 |
|
Радиус заготовки R1, мм |
40 |
|
Радиус заготовки R2, мм |
48 |
|
Частота тока источника питания f, кГц |
50 |
|
Шаг расчета модели, с |
0,1 |
На рис. 1, а представлена геометрия системы «индуктор – заготовка» с витками сложной формы, где штриховкой показана область закаливаемого слоя.
а
б
Рис. 1. Геометрия системы
«индукционный нагреватель – стальная заготовка»:
а – общий вид заготовки; б – заготовка и витки индуктора: R1, R2, R8, H – параметры геометрии заготовки;p1–p6 – оптимизируемые конструктивные параметры
Fig. 1. Geometry of the system “inductor-steel billet”:
a – general view of the billet geometry; б – billet and inductor coils: R1, R2, R8, H – parameters of the billet; p1–p6 – optimized design parameters
Рис. 1, б демонстрирует конструктивные особенности витков индуктора и их основные параметры, оптимальные значения которых необходимо определить в ходе решения.
Узлы A–F (рис. 2) представляют собой опорные точки на границе упрочняемого слоя, представляющие границы отрезков, сумма которых равна длине L упрочняемого слоя.
Рис. 2. Осесимметричная 2D модель системы «индукционный нагреватель – стальная заготовка»
c наложенной конечно-элементной сеткой в ППП ANSYS Mechanical APDL
Fig. 2. Axisymmetric 2D model of the “inductor-steel billet” system with superimposed finite element mesh
in ANSYS Mechanical APDL
Глубина закаливаемого слоя от поверхности на участках AB, CD, EF составляет 2 мм, BC – не менее 1 мм.
Получение наилучшего качества процесса закалки достигается за счет формирования равномерного температурного распределения в поверхностном слое заготовки в конце нагрева, которое позволит снизить термические напряжения и получить более равномерную микроструктуру. Однако использование типичных конструкций витков индукционных нагревателей и их режимов работы недостаточно. По этой причине возникает необходимость поиска оптимальных значений параметров индуктора и постановки задачи оптимизации.
В этой связи особую важность приобретает задача оптимизации конструктивных параметров нагревателя и алгоритмов управления режимами нагрева, постановка и решение которой рассматривается в последующих разделах.
Постановка и стратегия решения задачи совместной оптимизации проектных решений
и режимов функционирования индуктора
Постановка и решение совокупной задачи поиска оптимальных конструктивных параметров (оптимального проектирования) и алгоритмов управления (оптимального управления) объектом с распределенными параметрами (ОРП) позволяет выбрать такие проектные и режимные решения, которые способствуют достижению максимального эффекта по выбранному показателю качества или комплексному критерию эффективности [8]. Рассмотрим формулировку задачи совместной параметрической оптимизации конструкции и алгоритмов управления индуктором для нагрева под поверхностную закалку, в которой процесс индукционного нагрева рассматривается в качестве ОРП, описываемого системой взаимосвязанных нелинейных уравнений для электромагнитных, температурных полей и полей термических напряжений. Модель ОРП представляет собой нелинейную двумерную численную модель, разработанную в ANSYS Mechanical APDL [7], рассмотренную в предыдущем разделе.
Пусть оптимизируемые параметры конструкции индуктора включены в вектор 
а оптимизируемые режимные параметры представляют вектор 
Тогда суммарный вектор 
искомых параметров в задаче совместной оптимизации имеет повышенную, по сравнению с векторами 
и представляет собой совокупность векторов конструктивных и режимных параметров 
с 
составляющими параметрического представления проектных решений и управляющих воздействий [8] соответственно.
В рассматриваемой задаче вектор 
оптимизируемых конструктивных параметров включает следующие геометрические характеристики витков индуктора (см. рис. 1, б): p1 – расстояние между витком 1 и координатой Y = 0; p2 – координата
x точки Q витка 2; p3 – y-координата точки Q витка 2; p4 – расстояние между витком 3 и заготовкой;
p5 – расстояние между витком 1 и заготовкой;
p6 – расстояние от верхней части выступа детали до витка 3. Вектор 
включает параметр 
процесса, наиболее существенно влияющий на управление режимом нагрева – силу тока индуктора I. Тогда расширенный вектор параметров в задаче совместной оптимизации может быть представлен как 
а управляемое температурное распределение, зависящее от суммарного вектора 
конструктивных и режимных параметров, обозначим 
, где x, y – пространственные координаты, t – время.
На выбранные режимные и конструктивные параметры накладываются ограничения вида
(1)
Требование к результирующему температурному распределению в поверхностном слое заготовки в конце стадии предварительного нагрева металла под закалку целесообразно сформулировать в виде задания максимально допустимой величины ε абсолютного отклонения результирующего температурного распределения вдоль границы закаливаемого слоя 
от заданного значения температуры Tdes, где X – толщина упрочняемого поверхностного слоя; l – координата точки на границе ABCDEF упрочняемого слоя длиной L; 
– момент окончания стадии нагрева 
. Тогда в качестве целевой функции в задаче совместной оптимизации рассмотрим критерий, обеспечивающий минимальное абсолютное отклонение температурного распределения 
вдоль границы закаливаемого слоя в конце стадии нагрева от заданного значения Tdes [8, 9]:
, (2)
где температурное распределение 
может быть получено с помощью модели, разработанной в ППП ANSYS [8, 9].
Задача совместной оптимизации проектных решений и режимов функционирования индукционной нагревательной установки заключается
в поиске таких значений параметров 
на которые наложены ограничения (1), обусловленные характеристиками нагревательной системы, которые за установленное время обеспечат перевод объекта, описываемого нелинейной численной двумерной ANSYS-моделью, из исходного состояния в требуемое конечное состояние, соответствующее минимальному значению критерия оптимизации (2) [9].
Скоростной индукционный нагрев заготовки до температур выше точки Кюри может привести к локальным перегревам поверхностного слоя, что является нарушением технологии и приведет к ухудшению качества конечной продукции. Следовательно, при постановке задачи необходимо рассмотреть фазовое ограничение на максимально допустимое значение температуры по объему поверхностного слоя, которое может быть представлено в общем виде 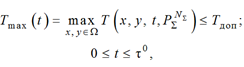(3):
(3)
где Ω представляет множество точек в пределах поверхностного слоя заготовки сложной формы. При нарушении ограничения (3), т. е. при обнаружении локального перегрева закаливаемого слоя, для его устранения необходимо перейти к решению задачи управления на интервале, в пределах которого температуры превышают допустимое значение Тдоп, который называется особым участком [9]. При решении задачи поиска алгоритма управления на особом участке для каждого шага расчета процесса осуществляется поиск такого управляющего воздействия, при котором выполняется условие
(4)
где t1, t2 – моменты начала и окончания особого участка управления соответственно.
Поскольку за счет введения особого участка управления на стадии нагрева равномерность температурного распределения вдоль границы закаливаемого слоя может снизиться, возникает необходимость повторного решения задачи совместной параметрической оптимизации для уточнения вектора оптимизируемых параметров с учетом найденного алгоритма управления на особом участке. Общая схема итерационной процедуры решения задачи совместной оптимизации с учетом фазового ограничения на максимально допустимую температуру представлена на рис. 3.
Рис. 3. Стратегия решения задачи совместной оптимизации с учетом фазового ограничения
Fig. 3. Strategy for solving the joint optimization problem with the phase limitation
Таким образом, стратегия оптимизации сводится к последовательному итерационному решению задачи совместной оптимизации без учета фазового ограничения (3), проверке выполнения условия (4) и решению задачи поиска алгоритма управления для обеспечения выполнения этого ограничения в случае его нарушения.
Альтернансный метод решения задачи оптимизации
Сформулированную задачу совместной параметрической оптимизации конструкции и алгоритмов управления индуктором для нагрева под поверхностную индукционную закалку стальных заготовок сложной формы предлагается решать с использованием альтернансного метода параметрической оптимизации систем с распределенными параметрами. Метод основан на универсальных свойствах пространственных распределений температурных полей по объему заготовки в конце оптимальных процессов индукционного нагрева и по-
зволяет свести исходную оптимизационную задачу к решению системы трансцендентных уравнений, сформулированных относительно всех неизвестных параметров процесса [9–11].
Согласно теории альтернансного метода, вдоль границы закаливаемого слоя найдутся M точек с координатами 
в которых достигаются предельно допустимые отклонения температуры 
в конце оптимальной стадии нагрева от заданного значения Tdes, где 
– вектор оптимальных параметров, полученный в результате решения задачи совместной оптимизации.
Эти температурные отклонения равны ε и представляют собой знакочередующиеся отклонения 
всегда равно или больше числа NΣ оптимизируемых параметров. В случае, когда ε совпадает с минимально достижимым в задаче с NΣ оптимизируемыми параметрами значением 
, между значениями NΣ и M существует зависимость, определяемая выражением M = NΣ + 1. Сказанное позволяет записать систему уравнений для поиска оптимальных значений параметров, составляющих вектор 
, в следующем виде [9–11]:
В описываемой задаче совместной оптимизации проектных решений и режимов функционирования индуктора вектор состоит из семи оптимизируемых параметров (NΣ = 7). Согласно альтернансному методу, число точек, в которых достигаются предельные отклонения 
температуры 
от заданного значения 
, равно M = NΣ + 1 = 8. При этом из физических соображений очевидно, что первый температурный минимум достигается на верхнем торце заготовки в точке А с координатой 
.
Как указывалось ранее, для реализации процедуры оптимизации в качестве требуемого конечного состояния ОРП рассматривается температурное распределение вдоль пространственной границы ABСDEF закаливаемого слоя, которую предлагается рассматривать как развертку по пространственной координате l
, (см. рис. 2). На рис. 4 представлено конечное распределение температуры 
вдоль границы упрочненного слоя ABCDEF, соответствующее оптимальному в конце стадии нагрева.
Рис. 4. Профиль оптимального конечного распределения температуры для задачи оптимизации
с семью оптимизируемыми параметрами и точностью нагрева 
Fig. 4. Profile of the optimal final temperature distribution for the optimization problem
with seven optimized parameters and heating accuracy 
Общая система уравнений для решения сформулированной задачи совместной оптимизации проектных решений и режимов функционирования индуктора для оптимального конечного распределения температуры 
, представленного на рис. 4, принимает вид [9–11]
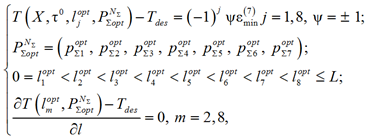(5)
где ψ – коэффициент, равный +1 или –1, учитывающий два возможных варианта отклонений по знаку в каждой из таких точек; – значение максимально достижимой точности нагрева в задаче оптимизации при NΣ = 7; 
соответствует точке А на верхнем торце заготовки (см. рис. 2); 
– координаты точек экстремумов. На выбранные режимный и конструктивные параметры накладываются ограничения (1).
Система (5) из 15 уравнений замкнута относительно 15 неизвестных параметров, в числе которых 7 оптимизируемых параметров, входящих в вектор 
и подчиненных ограничениям (1), 7 координат-точек экстремума 
с максимальным отклонением температуры, и сама величина отклонения 
.
Решение задачи совместной оптимизации проектных решений и режимов функционирования индуктора без учета фазового ограничения
Задача совместной оптимизации проектных решений и режимов функционирования индуктора решается с помощью разработанного в ППП MATLAB программного комплекса [12–14], который позволяет реализовать решение системы уравнений, сконструированной согласно альтернансному методу, с помощью стандартных функций оптимизации. Для вычисления температурных отклонений 
при решении системы уравнений производится обмен данными между ППП MATLAB и интегрированной конечно-элементной проблемно-ориентированной моделью стадии нагрева, разработанной в ANSYS Mechanical APDL. Полученные в результате решения задачи значения оптимизируемых параметров представлены в табл. 2.
Таблица 2
Table 2
Решение задачи совместной оптимизации без учета фазового ограничения
Solving the problem of joint optimization without phase limitation
Оптимальное температурное распределение вдоль границы закаливаемого слоя ABCDEF в конечный момент стадии нагрева представлено на рис. 5.
Рис. 5. Оптимальное распределение температуры в конце стадии нагрева вдоль границы закаливаемого слоя
Fig. 5. Optimum temperature distribution at the end of the heating stage along the boundary of the hardened layer
Для анализа температурного распределения, полученного в конце оптимального процесса нагрева, выбраны 7 характерных точек на поверхности заготовки, показанных на рис. 6, а.
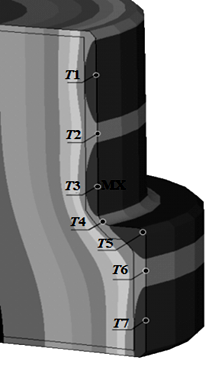
Рис. 6. Температурное распределение в конце оптимального процесса нагрева: а – расположение характерных точек:
Т1– Т 7 – точки на поверхности заготовки,в которых анализируются изменения температуры;Тдоп – предельно допустимая температура
Fig. 6. Temperature distribution at the end of the optimal process of heating: a – positions of specific dots:
T1–T 7 – points on the surface of the workpiece
in which temperature changes were analyzed;
Tдоп – maximum permissible temperature
Рис. 6 (окончание). Температурное распределение в конце оптимального процесса нагрева:
б – зависимость изменения температуры от времени
Fig. 6 (ending). Temperature distribution at the end of the optimal process of heating:
б – dependence of temperature change on time
На первом этапе решения задачи совместной оптимизации не учитывались ограничения (3) на максимальную допустимую температуру в процессе нагрева, поэтому для проверки выполнения этого ограничения необходимо исследование температуры в указанных точках, в которых ожидается наибольший перегрев. Динамика изменения температуры в характерных точках в процессе нагрева представлена на рис. 6, б.
Анализ рис. 6, б показывает, что при полученных в результате решения совместной задачи оптимизации значениях конструктивных и режимных параметров (см. табл. 2) в начале процесса отмечается интенсивный нагрев, при этом максимальная скорость нагрева наблюдается в точке Т3.
Температура в этой точке в определенный момент времени достигает предельно допустимого значения Тдоп = 1 050 °С, а затем продолжает возрастать до значения 1 130 °С, что означает нарушение технологического ограничения (3). При превышении допустимой температуры в процессе индукционного нагрева под поверхностную закалку в стальных заготовках могут возникнуть повышенные термические напряжения, которые приводят к появлению деформации геометрии заготовки, микротрещинам, обезуглероживанию, повышенному окислению поверхности и ухудшению качества и равномерности микроструктуры.
Для устранения наблюдаемого локального перегрева поверхности заготовки в соответствии с разработанной выше стратегией необходимо перейти
к решению задачи поиска алгоритма управления на особом участке нарушения ограничения (3), на каждом временном отрезке которого осуществляется поиск такого управляющего воздействия, при котором выполняется движение по ограничению на максимальную допустимую температуру поверхности Тдоп по условию (4).
Решение задачи поиска алгоритма управления стадией нагрева с учетом ограничений на максимальную допустимую температуру
При решении задачи совместной оптимизации
проектных решений и режимов функционирования индуктора установлено (см. рис. 6, б), что на интервале времени с t1 = 1 c до момента времени
t2 = 4,5 c максимальная температура превышает допустимое технологическое ограничение Тдоп. Это вызывает необходимость поиска такого управляющего воздействия, при котором температура на особом участке не будет превышать ограничение Тдоп. В [9, 15] показано, что алгоритм управления током индуктора на стадии нагрева для задачи
с фазовым ограничением для одного особого участка имеет вид
где IOY(t) – управление на особом участке движения по ограничению, а значение Iopt найдено на этапе решения задачи совместной параметрической оптимизации.
Поиск управляющего воздействия IOY(t) на особом участке представляет последовательный расчет значений силы тока на каждом временном шаге длительностью 0,1 с из условия выполнения ограничения (4). Для численного расчета IOY(t) используется стандартная функция ППП MATLAB, позволяющая на каждом временном шаге найти такое значение силы тока, которое обеспечивает минимальное значение температурного отклонения 
в соответствии с условием (4) [9, 15, 16].
Полученный в результате решения задачи алгоритм управления с учетом ограничения на максимально допустимую температуру Тдоп принимает вид
где IOY(t) представляет алгоритм управления на особом участке, показанный на рис. 7.
Рис. 7. Алгоритм управления и максимальная температура в процессе нагрева
с учетом фазового ограничения и выполнения условия (4)
Fig. 7. Control algorithm and maximum temperature during heating
with the phase limitation and the fulfillment of condition (4)
Алгоритм управления на особом участке (t1, t2) представляет собой ступенчато-постоянную функцию изменения силы тока на витках индуктора, при котором максимальная температура заготовки в закаливаемом слое равна предельно допустимому значению Тдоп.
Введение особого участка управления приводит к увеличению неравномерности температурного распределения вдоль границы закаливаемого слоя (рис. 8, кривая 1) в конце стадии нагрева, что вызывает не только ухудшение качества сформированной мартенситной микроструктуры в локальных зонах изделия, но и невозможность ее формирования в нижней части детали.
Рис. 8. Температурные распределения вдоль границы закаливаемого слоя до (кривая 1) и после (кривая 2)
повторного решения задачи совместной оптимизации с учетом ограничения (3)
Fig. 8. Temperature distributions along the boundary
of the solution quenched before (curve 1) and after (curve 2) of the repeated solution of the joint optimization problem subject to the constraint (3)
В этом случае в соответствии с разработанной стратегией оптимизации следует перейти к повторному решению совместной задачи параметрической оптимизации с учетом найденного алгоритма управления на особом участке.
Решение задачи совместной параметрической оптимизации с учетом фазового ограничения на максимальную допустимую температуру
При повторном решении задачи совместной оптимизации учитывается алгоритм управления на особом участке движения по ограничению (4). Значение сила тока 
уточняется на интервале
с 4,5 с до конца нагрева. Результаты расчетов задачи совместной оптимизации представлены на рис. 9.
Рис. 9. Алгоритм управления и зависимость температуры от времени в опорных точках в процессе нагрева
Fig. 9. Control algorithm and time dependence of temperature at reference points during heating
Сравнивая температурные распределения до (см. рис. 8, кривая 1) и после (см. рис. 8, кривая 2) повторного решения задачи совместной оптимизации с учетом технологического ограничения на максимальную допустимую температуру, можно отметить улучшение равномерности температурного распределения по границе закаливаемого слоя.
В табл. 3 и 4 представлено сравнение результатов решения задачи совместной оптимизации без учета технологического ограничения с повторным решением задачи совместной оптимизации с учетом технологического ограничения.
Таблица 3
Table 3
Оптимальные значения параметров на основе учета фазового ограничения Тдоп
Optimal parameter values with considering technological constraints Tadm
Таблица 4
Table 4
Координаты точек с максимальными отклонениями температур
Coordinates of points with maximum temperature deviations
|
Показатель |
l2 |
l3 |
l4 |
l5 |
l6 |
l7 |
l8 |
|
мм |
|||||||
|
Задача совместной оптимизация без учета ограничения (3) |
7,85 |
15,91 |
24,35 |
28,44 |
36,96 |
42,12 |
52,26 |
|
Задача совместной оптимизация с учетом ограничения (3) |
7,88 |
15,88 |
24,35 |
28,43 |
36,92 |
41,99 |
51,83 |
Решение задачи совместной оптимизации с учетом найденного алгоритма управления позволяет нагреть представленную заготовку равномерно и без перегревов поверхности. Полученные абсолютные значения отклонений конечной температуры от заданной не превышают 40,58 °C. Это отклонение проверяется по диаграмме аустенитного превращения, согласно которой для аналогичной стали марки 45 анализируемое значение находится в интервале температур выше линии AC3 [17], при которых формируется аустенитная микроструктура вдоль обозначенной границы закаливаемого слоя. Это свидетельствует о том, что было получено температурное отклонение, которое отвечает технологическим требованиям.
Заключение
Детальный анализ результатов решения задачи совместной оптимизации без учета технологического ограничения позволил выявить область, в которой наблюдались значения температур, превышающие предельно допустимые технологические требования в процессе нагрева. Последовательное решение задачи поиска алгоритма управления на особом участке, а также совместной оптимизации с учетом технологического ограничения на максимально допустимые температуры при помощи альтернансного метода позволило определить значения конструктивных и режимных параметров индуктора, при которых обеспечивается достаточная равномерность температурного поля вдоль границы закаливаемого слоя заготовки сложной геометрической формы в конце стадии нагрева при отсутствии недопустимых перегревов на всем протяжении процесса.
1. Pleshivtseva Y., Pavlushin A., Popov A. Optimal Design of Inductor Coils for Surface Hardening // 2022 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM). IEEE, 2022. P. 680-685.
2. Pavlushin A. V. Problemno-orientirovannaya model' tehnologicheskogo processa poverhnostnoy indukcionnoy zakalki // Vestn. Samar. gos. tehn. un-ta. Ser.: Tehnicheskie nauki. 2022. T. 30. № 2 (74). S. 21-34.
3. Dossett J., Totten G. E. ASM Handbook. Volume 4A: Steel Heat Treating Fundamentals and Processes. ASM Intern, 2013. URL: https://pdfslide.us/documents/asm-handbook-volume-4a-steel-heat-treating-fundamentals-and-.html?page=7 (data obrascheniya: 31.03.2023).
4. Rudnev V., Loveless D., Cook R. L. Handbook of induction heating. CRC press, 2017. URL: https://www.routledgehandbooks.com/doi/10.1201/9781315117485-3 (data obrascheniya: 31.03.2023).
5. Pavlushin A. V. Optimizaciya konstruktivnyh i rezhimnyh parametrov indukcionnoy nagrevatel'noy ustanovki dlya zakalki // Vestn. Samar. gos. tehn. un-ta. Ser.: Tehnicheskie nauki. 2021. T. 29. № 3 (71). S. 38-51.
6. Ansys // Engineering Simulation Software: sayt programmnogo produkta ANSYS. URL: https://www.ansys.com/ (data obrascheniya: 31.03.2023).
7. Marochnik staley i splavov / pod red. Yu. G. Dragunova, A. S. Zubchenko i dr. M.: 2014. 1216 s. URL: https://www.mashin.ru/files/stranicy_iz_marochn15.pdf (data obrascheniya: 31.03.2023).
8. Rapoport E. Ya., Pleshivceva Yu. E. Metody polu-beskonechnoy optimizacii v prikladnyh zadachah upravleniya sistemami s raspredelennymi parametrami: monogr. M.: Nauka, 2021. 286 s.
9. Rapoport E. Ya., Pleshivceva Yu. E. Optimal'noe upravlenie temperaturnymi rezhimami indukcionnogo nagreva. M.: Nauka, 2012. 309 c.
10. Rapoport E. Ya. Al'ternansnyy metod v prikladnyh zadachah optimizacii. M.: Nauka, 2000. 336 c.
11. Pleshivceva Yu. E., Popov A. V., Popova M. A., Derevyanov M. Yu. Optimal'noe proektirovanie induktora dlya poverhnostnoy zakalki cilindricheskih zagotovok na osnove chislennoy dvumernoy modeli // Vestn. Astrahan. gos. tehn. un-ta. Ser.: Upravlenie, vychisli-tel'naya tehnika i informatika. 2019. № 1. S. 40-50.
12. MATLAB Documentation: sayt dokumentacii MATLAB. URL: https://www.mathworks.com/help/matlab/ (data obrascheniya: 02.04.2023).
13. Pleshivtseva Y., Popov A., Pavlushin A. New Ap-proach to Optimization of Surface Induction Hardening Process // 2022 4th International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA). IEEE, 2022. P. 525-530.
14. Pleshivtseva Y., Popov A., Pavlushin A. Software solution for optimal design of inductor for surface hardening // 2021 3rd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA). IEEE, 2021. P. 646-649.
15. Popov A. V. Optimizaciya stadii nagreva v processe indukcionnoy zakalki cilindricheskih zagotovok // Problemy upravleniya i modelirovaniya v slozhnyh sistemah: tr. XXI Mezhdunar. konf. (Samara, 03-06 sentyabrya 2019 g.): v 2 t. Samara: OOO «Ofort», 2019. S. 92-97.
16. Popov A. V., D'yakonov A. I. Optimal'noe po bystrodeystviyu upravlenie processom periodicheskogo indukcionnogo nagreva s uchetom ogranicheniya na maksimal'nuyu temperaturu // Vestn. Samar. gos. tehn. un-ta. Ser.: Tehnicheskie nauki. 2015. № 3 (47). S. 56-68.
17. Orlich J., Rose A., Wiest P. Atlas zur Wärmebehandlung der Stähle: Band 3: Zeit, Temperatur, Austentisierung, Schaubilder. Düsseldorf: Verlag Stahleisen, 1973. 264 p.
