Astrahan', Astrakhan, Russian Federation
Russian Federation
Russian Federation
The article considers the issues of analyzing data that the consumer encounters when choosing products and services. The problem is extracting useful information that allows offering the user new products and services depending on his preferences. This problem is localized by recommender systems focused on using the data mining methods, such as classification, clustering, analysis of association rules - a machine learning method that detects relationships between variables in databases. Compared to other methods, the advantage of the association rule-based recommender method is its transparency: the method can show the user the inference mechanism used to make decisions. Association rule-based recommender systems use two measures that are widely popular and evaluate sets of elements and create sets of association rules, the support measure and the confidence measure. However, to get better recommendations, the quality of association rules and the way sentence ranking should be measured by some objective measure. There has been developed a model and a decision support algorithm for the choice of products for recommendations to the user based on the statistical implication analysis method. In the proposed solutions, support and credibility measures are used to create association rules; a measure of the intensity of the statistical implication is used to filter the set of rules and to rank the recommendations.
search, user, product, recommender system, recommender model, statistical implication intensity, Apriori algorithm, association rule
Введение
Современные поисковые системы сталкиваются с растущими вызовами: очень сложно найти полезную информацию для принятия решения при большом количестве вариантов за короткое время. Тенденция перехода от информационного поиска к информационно-рекомендательным советам осуществляется весьма быстро. Рекомендательная система стала крайне необходимым и широко используемым инструментом в сфере информационных технологий, коммерции, электронных услуг (AliExpress, Amazon, Pandora, Netflix, Walmart и т. д.). Цель рекомендательной системы состоит в том, чтобы отфильтровать полезную информацию из большого количества информации для возможности предсказания рейтинга, который пользователь присвоит элементу-продукту, и рекомендовать подходящие элементы [1–3].
Среди алгоритмов рекомендательных систем одним из самых успешных является совместная фильтрация. В то же время не существует внутренних проблем при выработке рекомендаций, если считать, что взаимное влияние пары пользователей симметрично [3]. Однако на практике роли и взаимодействия между двумя пользователями часто асимметричны. Это может создать определенную предвзятость в рекомендациях, т. к. более опытный пользователь, например эксперт, входящий в систему, имеет большее влияние на другого, а другой (менее опытный или новичок) не сможет достичь противоположного эффекта. Существующие рекомендательные системы сосредоточены только на логическом решении вопроса о наличии или отсутствии взаимосвязи между пользователем и продуктами, однако не используют импликативное отношение «если А, то В» между ними, определяя степень соответствия на основе статистических данных о взаимозависимостях между пользователями и выбранными продуктами [4]. В данном случае импликативное отношение рассматривается как отношение, основанное на знаниях о связях между пользователем и элементами данных, необходимых для выработки рекомендации. Таким образом, использование метода асимметричного подхода представляет большой интерес для минимизации систематической ошибки из-за указанного выше различия в результатах рекомендаций. Применение метода анализа статистической импликации в области рекомендательных систем необходимо для учета асимметричного влияния пользователей и оценки импликативной связи между пользователем и продуктами на практике.
Определение меры интенсивности статистической импликации
Метод анализа статистической импликации [4, 5] – это метод анализа данных, который позволяет обнаружить правила a → b (a – атрибуты объектов, принадлежащих множеству А; b – атрибуты объектов во множестве B) в асимметричной форме «если a, то почти b» или «в какой степени b соответствует импликации a». Предположим, что набор E имеет n объектов или индивидов, описывается конечным набором бинарных переменных (атрибутов). Пусть 
– подмножество объектов, удовлетворяющих атрибутам a; 
– подмножество объектов, удовлетворяющих атрибутам b; 
(соответственно,
) является дополнением A (соответственно, B); 
– количество элементов множеств A и B; число контрпримеров 
– это число объектов, которые удовлетворяют свойству a, но не удовлетворяют свойству b. Пусть X и Y – два случайных набора с количеством элементов nx = nA и ny = nB соответственно. Предположим, что в процессе выборки случайная величина 
следует распределению Пуассона с параметром
Правило a → b называется приемлемым для заданного порога α, если
где Pr – вероятность случайной величины.
Рассмотрим случай 
. Тогда согласно распределению Пуассона вероятность случайной величины определяется следующим образом:
В эксперименте наблюдаемое значение 
для 
определяется следующим образом:
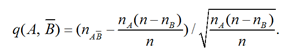
Это значение называется индексом статистической значимости.
Мера интенсивности статистической импликации φ(a, b) правила a → b определяется формулой
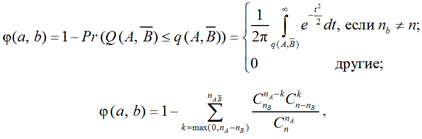
где k – целое число.
Эта мера используется для определения контрпримеров в наборе E. Значение меры интенсивности статистической импликации φ(a, b) принимается с заданным порогом α, если φ(a, b) ≥ 1 – α.
Рекомендательная модель на основе меры интенсивности статистической импликации
Рекомендательная модель совместной фильтрации при поддержке принятия решений при выборе продуктов пользователем может быть представлена в виде следующей совокупности объектов:
RS = {U, I, R, F},
где 
– набор из n пользователей; 
– набор из m продуктов; 
– матрица рейтингов пользователей, где rj,k – значение рейтинга пользователя uj для продукта ik; 
– это вычислительная функция для поиска набора продуктов 
для рекомендации пользователей ua.
Основными компонентами рекомендательных методов являются меры, используемые для поиска похожих пользователей, поиска похожих продуктов, выявления отношений с высоким уровнем вовлеченности или ранжирования рекомендаций
и т. д. В предлагаемой модели показатели «поддержка» (англ. Support) и «достоверность» (англ. Confidence) используются для создания набора правил, а мера интенсивности статистической импликации используется для ранжирования набора правил. Основным входом предлагаемой модели является рейтинговая матрица, в которой хранится важная информация, генерируемая в процессе взаимодействия пользователя с системой, например рейтинг пользователя для просмотренных фильмов или прослушанных песен. Рейтинговая матрица может иметь пустые ячейки (отсутствуют рейтинги), если пользователь uj не ставил оценку продукту ik или не знает об этом.
Процесс работы предлагаемой модели показан на рис. 1.
На основе модели разработана методика поддержки принятия решения по выбору продуктов для рекомендации пользователю. В методике выделены 5 основных этапов.
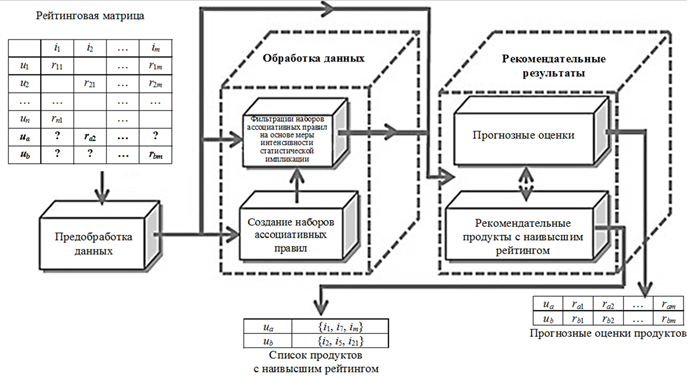
Рис. 1. Основные этапы обработки рекомендательной модели
на основе меры интенсивности статистической импликации
Fig. 1. Main stages of processing the recommender model based
on the measure of intensity of the statistical implication
Этап 1: предварительная обработка данных. Этот этап состоит из двух подзадач: 1) выбор соответствующих данных (в наборе данных) определением минимального количества элементов, оцененных каждым пользователем, и минимального количества пользователей, выполняющих обзор каждого элемента; 2) приведение к бинарному виду выбранного набора данных, если это не двоичные данные. Результатом этого этапа является набор данных (dataset).
Этап 2: создание набора ассоциативных правил ruleset из набора данных dataset. Этот этап состоит из двух подзадач: 1) выбор порога для 2-х показателей (поддержка и достоверность); 2) генерация набора ассоциативных правил на основе пороговых значений показателей (поддержка и достоверность) с использованием алгоритма Apriori [6]. Этот набор правил включает правила с максимальной длиной l и минимальной 2. Если правило имеет длину l, то оно будет иметь l – 1 элементов слева и l элемент справа.
Этап 3: создание набора правил фильтрацией набора правила ruleset на основе меры интенсивности статистической импликации. Этот этап состоит из трех подзадач: 1) представление каждого правила набором из 4-х значений ; 2) вычисление значения меры интенсивности статистической импликации каждого правила; 3) выбор соответствующего порога меры интенсивности статистической импликации для уменьшения набора правил.
Этап 4: поиск наиболее релевантного продукта для пользователей в наборе данных recset (это набор данных из р пользователей с отсутствием некоторых рейтингов). Этот этап состоит из двух подзадач:
1) для каждого пользователя найти правила, левая часть которых является подмножеством множества продуктов, которые оценены этим пользователем;
2) ранжировать (сортировать) отфильтрованные правила в соответствии со значением меры интенсивности статистической импликации и найти N предметов с наивысшим рейтингом.
Этап 5: прогноз рейтинга для отсутствующих оценок. Этот этап состоит из двух подзадач: 1) для каждой отсутствующей оценки в строке i и столбце j найти правила, у которых левая часть является подмножеством набора элементов, оцененных пользователем i, а правая часть является элементом j;
2) ранжировать (сортировать) отфильтрованные правила в соответствии со значением меры интенсивности статистической импликации, затем присвоить отсутствующему рейтингу значение 0 или 1 на основе определенного порога.
В данной статье существенно раскрываются этапы 2, 5.
Детализируем некоторые сложносоставные этапы. Для реализации этапа 2 предложен алгоритм создания набора ассоциативных правил из набора обучающих данных. Вначале алгоритм генерирует наборы из 1 элемента, набора из 2 элементов, ..., набора из k элементов. Затем для каждого набора
из k элементов генерируются непустые подмножества. Наконец, из этих подмножеств создаются ассоциативные правила на основе порогового значения меры интенсивности статистической импликации. Этот порог определяется на основе экспериментальных результатов конкретных наборов данных. Алгоритм формирования ассоциативных правил, основанный на мере интенсивности статистической импликации, представлен на рис. 2.
Рис. 2. Алгоритм формирования ассоциативных правил,
основанный на мере интенсивности статистической импликации
Fig. 2. Algorithm for developing association rules
based on the measure of intensity of the statistical implication
Псевдокод алгоритма формирования правил ассоциации, основанный на мере интенсивности статистической импликации.
Входные данные: набор обучающих данных и пороговое значение меры интенсивности статистической импликации.
Выходные данные: набор ассоциативных правил, основанный на мере интенсивности статистической импликации.
Начало.
Шаг 1. Сгенерировать наборы из 1 до k элементов:
<Создать набор из 1 элемента обучающих данных >;
<Создать набор из 2 элементов из набора из
1 элемента>;
…
<Создать набор из k элементов из набора из
k – 1 элементов>.
Шаг 2. Создать непустые подмножества для каждого набора кандидатов. Для каждого набора кандидатов I выполнить следующую операцию:
<Создать непустые подмножества >.
Шаг 3. Сгенерировать ассоциативные правила
с порогом меры интенсивности статистической импликации. Для каждого непустого подмножества выполнить следующую операцию:
<Создать ассоциативное правило >.
Если значение меры интенсивности статистической импликации ассоциативного правила r больше, чем порог меры интенсивности статистической импликации, то:
<Выбрать ассоциативное правило r для рекомендательной модели>.
Конец.
Пример 1. Использовать рейтинговую матрицу для 2 пользователей и 4 продуктов следующим образом (табл. 1).
Таблица 1
Table 1
Рейтинговая матрица
для 2 пользователей и 4 продуктов
Rating matrix for 2 users and 4 products
|
Продукт Пользователь |
i1 |
i2 |
i3 |
i4 |
|
u1 |
0 |
4 |
4 |
1 |
|
u2 |
0 |
0 |
4 |
1 |
Для создания ассоциативных правил матрица рейтинга пользователя преобразуется в разреженную бинарную матрицу со следующей структурой (табл. 2).
Таблица 2
Table 2
Разреженная бинарная матрица рейтинга
Sparse binary rating matrix
|
i1 = 0 |
i2 = 4 |
i2 = 0 |
i3 = 4 |
i4 = 1 |
|
1 |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
1 |
1 |
Из разреженной бинарной матрицы определяются одноэлементные подмножества:
{i1 = 0},{i2 = 4}, {i2 = 0}, {i3 = 4}, {i4 = 1}.
Из 1-элементных подмножеств генерируются
2-элементные подмножества:
{i1 = 0, i2 = 4}, {i1 = 0, i2 = 0}, {i1 = 0, i3 = 4},
{i1 = 0, i4 = 1}, {i2 = 4, i2 = 0}, {i2 = 4, i3 = 4},
{i2 = 4, i4 = 1}, {i2 = 0, i3 = 4}, {i2 = 0, i4 = 1},
{i3 = 4, i4 = 1}.
Из 2-элементных подмножеств генерируются трехэлементные подмножества:
{i1 = 0, i2 = 4, i2 = 0}, {i1 = 0, i2 = 4, i3 = 4},
{i1 = 0, i2 = 4, i4 = 1}, {i1 = 0, i2 = 0, i3 = 4},
{i1 = 0, i2 = 0, i4 = 1}, {i1 = 0, i3 = 4, i4 = 1},
{i2 = 4, i2 = 0, i3 = 4}, {i2 = 4, i2 = 0, i4 = 1},
{i2 = 4, i3 = 4, i4 = 1}, {i2 = 0, i3 = 4, i4 = 1}.
Из 3-элементных подмножеств генерируются
4-элементные подмножества:
{i1 = 0, i2 = 4, i2 = 0, i3 = 4},
{i1 = 0, i2 = 4, i2 = 0, i4 = 1},
{i1 = 0, i2 = 4, i3 = 4, i4 = 1},
{i1 = 0, i2 = 0, i3 = 4, i4 = 1},
{i2 = 4, i2 = 0, i3 = 4, i4 = 1}.
Из 4-элементных подмножеств генерируются
5-элементные подмножества:
{i1 = 0, i2 = 4, i2 = 0, i3 = 4, i4 = 1}.
На основе полученных наборов приступаем
к генерации ассоциативных правил с порогом меры интенсивности статистической импликации φ(a, b) ≥ 0,3 и получаем 36 ассоциативных правил:
{i1 = 0} => {i2 = 4}, {i2 = 4} => {i1 = 0}, {i1 = 0} =>{i4 = 1},
{i4 = 1} => {i1 = 0}, {i2 = 4} => {i4 = 1}, {i4 = 1} => {i2 = 4},
{i1 = 2} => {i2 = 0}, {i2 = 0} => {i1 = 2}, {i1 = 2} => {i4 = 1},
{i4 = 1} => {i1 = 2}, {i2 = 0} => {i4 = 1}, {i4 = 1} => {i2 = 0},
{i1 = 0, i2 = 4} => {i4 = 1}, {i1 = 0, i4 = 1} => {i2 = 4},
{i2 = 4, i4 = 1} => {i1 = 0}, {i1 = 0, i3 = 4} => {i2 = 4},
{i2 = 4, i3 = 4} => {i1 = 0}, {i1 = 0, i3 = 4} => {i4 = 1},
{i3 = 4, i4 = 1} => {i1 = 0}, {i2 = 4, i3 = 4} => {i4 = 1},
{i3 = 4, i4 = 1} => {i2 = 4}, {i1 = 2, i2 = 0} => {i4 = 1},
{i1 = 2, i4 = 1} => {i2 = 0}, {i2 = 0, i4 = 1} => {i1 = 2},
{i1 = 2, i3 = 4} => {i2 = 0}, {i2 = 0, i3 = 4} => {i1 = 2},
{i1 = 2, i3 = 4} => {i4 = 1}, {i3 = 4, i4 = 1} => {i1 = 2},
{i2 = 0, i3 = 4} => {i4 = 0}, {i3 = 4, i4 = 1} => {i2 = 0},
{i1 = 0, i2 = 4, i3 = 4} => {i4 = 1}, {i1 = 0, i3 = 4, i4 = 1} => {i2 = 4},
{i2 = 4, i3 = 4, i4 = 1} => {i1 = 0}, {i1 = 2, i2 = 0, i3 = 4} => {i4 = 1},
{i1 = 2, i3 = 4, i4 = 1} => {i2 = 0}, {i2 = 0, i3 = 4, i4 = 1} => {i1 = 2}
Детализируем этап 5. Разработан алгоритм поддержки принятия решений по выбору продуктов для рекомендации пользователю на основе меры интенсивности статистической импликации.
Пусть U = {u1, u2, ..., un} – набор из n пользователей, I = {i1, i2, ..., im} – набор из m продуктов, RTrain = = {rj, k} – набор обучающих данных, где
rj, k – значение рейтинга пользователя uj для продукта ik в наборе обучающих данных; RTest = {ri, l} – набор тестовых данных, где ri, l – значение рейтинга пользователя ui для продукта il в наборе тестовых данных; RU = {r1, r2, ..., rt} – набор ассоциативных правил, сгенерированный из набора обучающих данных на основе меры интенсивности статистической импликации; MATRIXLogical = {bt, i} – логическая матрица, где bt, i – логическое значение проверки соответствия между правилом rt и пользователем ui: если пользователь ui имеет рейтинги продуктов в левой части правила rt, то bt, i = TRUE, иначе bt, i = FALSE, 
– набор ассоциативных правил, выбранных для пользователя ua. Результатом рекомендации для пользователя ua является набор продуктов, которые принадлежат правой части набора правил и эти продукты не оценены пользователем ua: .
Чтобы определить набор ассоциативных правил для каждого пользователя в наборе тестовых данных, вначале алгоритм использует данные о количестве ассоциативных правил, сгенерированных из набора обучающих данных, и количестве пользователей
в наборе тестовых данных для генерации логической матрицы, состоящей из t строк, l столбцов (t – количество правил, l – количество пользователей). Матрица создается следующим образом: если пользователь ui имеет рейтинги товаров в левой части правила rt, то ячейке (t, i) матрицы присваивается значение «TRUE» (bt, i = TRUE), в противном случае ей присваивается значение «FALSE» (bt, i = FALSE). Затем для каждого столбца i, если значение ячейки (t, i) равно «TRUE», выбирается соответствующее ассоциативное правило в строке t для пользователя i. Наконец, выбранные правила сортируются для каждого пользователя, для которого вырабатываются рекомендации, в порядке убывания величины меры интенсивности статистической импликации. В итоге выбираются N продуктов из правой части правил с наибольшим значением, для которых пользователь не имеет рейтингов для предоставления рекомендаций.
Псевдокод алгоритма поддержки принятия решений по выбору продуктов для рекомендации пользователю на основе меры интенсивности статистической импликации.
Входные данные: набор ассоциативных правил, генерируемый из набора обучающих данных, набор тестовых данных.
Выходные данные: рекомендации для каждого пользователя в тестовом наборе данных.
Начало.
Шаг 1. Создание логической матрицы на основе набора ассоциативных правил и набора тестовых данных:
t = <число ассоциативных правил>;
l = <число пользователей набора тестовых данных>;
, где i = {1, 2, ..., t}, j = {1, 2, ..., l}.
Для каждого выбранного ассоциативного правила выполнить:
Если ((Набор продуктов в левой части правила в строке i) (Набор продуктов, которые не оценены пользователем в столбце j) ), то:
.
В противном случае: .
Шаг 2. Выбор ассоциативных правил для каждого пользователя, с которым необходимо консультироваться.
Для каждого пользователя в тестовом наборе выполнить:
Если , то <Выбрать ассоциативное правило в строке i для пользователя в столбце j >).
Шаг 3. Выбрать продукты, по которым требуется консультироваться для каждого пользователя.
Для каждого пользователя в тестовом наборе выполнить:
<Сортировать правила в порядке убывания величины меры интенсивности статистической импликации>;
<Выбрать продукты справа от правила с наи-
высшим значением меры интенсивности статистической импликации, которые не оценены пользователем j, чтобы рекомендовать пользователю j >.
Конец.
Пример 2. Чтобы более четко увидеть этапы реализации модели, предположим, что система рекомендует пользователям выбрать 8 продуктов (от i1 до i8), система имеет 10 ранжированных пользователей (от u1 до u10). Рейтинги для продуктов, представленные бинарной матрицей, показаны в табл. 3.
Таблица 3
Table 3
Матрица рейтингов продуктов
Product rating matrix
|
Продукт Пользователь |
i1 |
i2 |
i3 |
i4 |
i5 |
i6 |
i7 |
i8 |
|
u1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
u2 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
|
u3 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
u4 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
|
u5 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
u6 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
|
u7 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
|
u8 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
u9 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
u10 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Данные делятся на два набора: обучающих данных (от u1 до u7); тестовых данных (от u8 до u10), каждый пользователь выбирает два продукта для рекомендации. Первым шагом является создание набора ассоциативных правил на основе меры интенсивности статистической импликации на наборе обучающих данных с порогом меры интенсивности статистической импликации φ(a, b) ≥ 0,5, т. е. 49 правил. Следующий шаг выполняется на основе набора ассоциативных правил и набора тестов для построения логической матрицы. Последний шаг – от логической матрицы до генерации результатов рекомендаций – представлен в табл. 4.
Таблица 4
Table 4
Наборы правил для каждого пользователя и продукты для рекомендации пользователю
Sets of rules for each user and products to be recommended to the user
|
Пользователь |
Ассоциативные правила |
Значение меры интенсивности статистической импликации |
Продукты для рекомендации |
|
u8 |
{i4, i5} => {i3}; {i1, i4} => {i7}; {i3, i4} => {i5}; {i4, i8} => {i5}; {i4} => {i7}; {i4} => {i5}; {i1, i3} => {i7}; {i3, i4, i8} => {i7}; {i4, i7, i8} => {i3}; {i1, i3, i8} => {i7}; {i1, i7, i8} => {i3}; {i4, i5, i7} => {i3}; {i1, i3, i5} => {i7}; {i1, i5, i7} => {i3}; {i1, i3, i4} => {i7};{i2, i4, i5} => {i3}; {i2, i5, i6} => {i3}; {i1, i2, i4} => {i7}; {i1, i2, i6} => {i7}; {i3, i4, i5, i8} => {i7}; {i4, i5, i7, i8} => {i3}; {i1, i3, i5, i8} => {i7}; {i1, i5, i7, i8} => {i3}; {i1, i3, i4, i8} => {i7}; {i1, i4, i7, i8} => {i3}; {i1, i3, i4, i5} => {i7}; {i1, i4, i5, i7} => {i3};{i2, i4, i5, i6} => {i3}; {i1, i2, i4, i6} => {i7}; {i1, i3, i4, i5, i8} => {i7}; {i1, i4, i5, i7, i8} => {i3} |
[0,63;0,51] |
i3, i7 |
|
u9 |
{i3, i4} => {i5}; {i3} => {i5}; {i3} => {i4}; {i7} => {i4}; {i3, i5} => {i4}; {i1, i7} => {i4}; {i1, i3} => {i7}; {i3, i4, i8}=>{i7}; {i4, i7, i8} => {i3}; {i1, i3, i8} => {i7}; {i1, i7, i8} => {i3}; {i4, i5, i7} => {i3}; {i1, i5, i7} => {i3}; {i1, i3, i4} => {i7}; {i2, i4, i5} => {i3}; {i2, i5, i6} => {i3};{i1, i2, i4} => {i7}; {i1, i2, i6} => {i7}; {i3, i4, i5, i8} => {i7}; {i4, i5, i7, i8} => {i3}; {i1, i3, i5, i8} => {i7}; {i1, i5, i7, i8} => {i3}; {i1, i3, i4, i8} => {i7}; {i1, i4, i7, i8} => {i3}; {i1, i3, i4, i5} => {i7}; {i1, i4, i5, i7} => {i3}; {i2, i4, i5, i6} => {i3}; {i1, i2, i4, i6} => {i7}; {i1, i3, i4, i5, i8} => {i7}; {i1, i4, i5, i7, i8} => {i3}; {i3, i8} => {i7}; {i7, i8} => {i3}; {i5, i7} => {i3}; {i3, i5, i8} => {i7}; {i5, i7, i8} => {i3}; {i2, i5} =>{ i3} |
[0,58; 0,51] |
i5, i4 |
|
u10 |
{i1, i4} => {i7}; {i3, i4} => {i5}; {i3} => {i5}; {i3} => {i4}; {i3, i5} => {i4}; {i4, i8} => {i5}; {i1, i5, i8} => {i4}; {i1, i4, i8} => {i5};{i1, i4, i5} => {i8}; {i5, i8} => {i4}; {i1, i3} => {i7}; {i3, i4, i8} => {i7};{i4, i7, i8} => {i3}; {i1, i3, i8} => {i7}; {i1, i7, i8} => {i3}; {i1, i5, i7} => {i3}; {i1, i3, i4} => {i7}; {i1, i2, i4} => {i7}; {i1, i2, i6} => {i7}; {i3, i4, i5, i8} => {i7}; {i4, i5, i7, i8} => {i3}; {i1, i3, i5, i8} => {i7}; {i1, i5, i7, i8} => {i3}; {i1, i3, i4, i8} => {i7}; {i1, i4, i7, i8} => {i3}; {i1, i3, i4, i5} => {i7}; i1, i4, i5, i7} => {i3}; {i1, i2, i4, i6} => {i7}; {i1, i3, i4, i5, i8}=>{i7}; {i1, i4, i5, i7, i8} => {i3}; {i3, i8} => {i7};{i7, i8} => {i3}; {i3, i5, i8} => {i7}; {i5, i7, i8} => {i3}; {i1, i3, i5} => {i7} |
[0,63; 0,51] |
i7, i5 |
Исходя из результатов рекомендации в табл. 4, обнаружены продукты для рекомендации пользователю u8 – {i3, i7}, для пользователя u9 – {i5, i4}, для пользователя u10 – {i7, i5}.
Заключение
Разработаны модель и алгоритм поддержки принятия решения по выбору продуктов для рекомендации пользователю на основе метода анализа статистической импликации. В модели и алгоритме показано, как определить набор ассоциативных правил на основе меры интенсивности статистической импликации, описаны шаги для построения рекомендательной модели на основе этого набора правил.
1. Shurshev V. F., Kochkin G. A., Kochkina V. R. Mo-del' sistemy podderzhki prinyatiya resheniy na osnove rassuzhdeniy po precedentamtehnika i informatika. 2013. № 2. S. 175-183.
2. Kvyatkovskaya I. Y., Shurshev V. F., Frenkel M. B. Methodology of a support of making management decisions for poorly structured problems // Communications in Computer and Information Science. 2015. V. 535. P. 278-291.
3. Nefedova Yu. S. Arhitektura gibridnoy rekomendatel'noy sistemy GEFEST (Generation-Expansion-Filtering-Sorting-Truncation) // Sistemy i sredstva informatiki. 2012. T. 22, vyp. 2. S. 176-196.
4. Gras R., Kuntz P. An overview of the Statistical Im-plicative Analysis (SIA) development // Statistical Implica-tive Analysis - Studies in Computational Intelligence. 2008. V. 127. P. 11-40.
5. Gras R., Kuntz P., Greffard N. Notion of Implicative Fields in Statistical Implicative Analysis // VIII Colloque International - VIII International Conference A.S.I. Analyse Statistique Implicative - Statistical Implicative Analysis Radès (Tunisie) - Novembre 2015. P. 29-46.
6. Shitikov V. K., Mastickiy S. E. Klassifikaciya, regressiya, algoritmy Data Mining s ispol'zovaniem R,2017. URL: https://github.com/ranalytics/data-mining (data obrascheniya: 07.01.2019).
