Russian Federation
Russian Federation
Russian Federation
An important task of mechanics of synthetic fishing twisted rope and string products and braided cords is to create a fundamental basis for describing their fracture processes during deformation in operation, i.e. to develop a framework for fracture mechanics (building models and algorithms for calculating structures and technological processes at large plastic deformations, taking into account fracture). There is considered the necessity of developing and introducing the simple and at the same time effective criteria of destruction, allowing to estimate reliably the conditions of safe operation of twisted rope and string products, threaded products and braided cords and especially the structures of industrial fishing gear. Determination of stress concentrations, is an obvious task in connection with the creation of new fishing trawls, purse seines and grips with complex shape-changing geometry. This problem is actual for many branches of industry, including transport and machine-building, where at the designing stage it is necessary to take into account possible emergency situations caused by intensive dynamic effects in twisted rope and string, threaded products and braided cords. Components and structures of twisted rope and string products, threaded products and braided cords should withstand the specified loads in a wide range of loading rates. In particular, the theory allows to solve nonlinear problems, taking into account changes in geometry of deformable twisted rope and string products, threaded products and braided cords, as well as to obtain analytical solutions of various problems.
load and break theory, mathematical model, rope-string product, calculation, braided cord, elasticity, plasticity, strength, synthetic fishing materials
Introduction
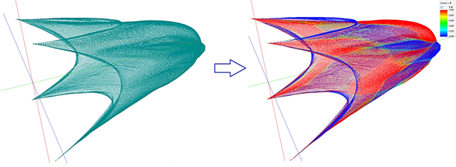
Among the physical and mechanical properties of fishing twisted rope and string products (RSP) and braided cords (BC), resistance of fluidity and fracture resistance are fundamental. Even in cases where other properties of solids are used in their operation (thermal, etc.) RSP and BC must be able to withstand maximum loads, preserving their integrity, shape and size. Rupture of RSP and BC leads to an emergency situation in the operation of the commercial fishing gear, especially trawls, purse seines, and hooks. Nowadays, the estimation of ultimate stresses (Fig. 1) in complex stressed state of industrial fishing tools and estimation of conditions of RSP and BC transition under load into ductile state is very problematic.
a b
Fig. 1. Grip:
a – grip; b – numerical modeling of loads in the grip
In this connection, studying the deformation and fracture mechanisms and improvement of methods for estimating the ultimate stresses and durability of RSP and BC, of which the majority of industrial fishing gears are made, is the actual problem of physics and mechanics of solid deformed bodies. Figure 1 shows a grip and numerical simulation of loads in the strings of the deli from which it is made at the corresponding rate of its sampling. Numerical simulation of loads in the grip was performed using the software System of Computer-Aided Design of Industrial Fishing Gears [1]. Physical and mechanical properties of RSP and BC are connected with their reaction to loading [2, 3], when stresses and deformations arise in fibers of RSP and BC. External load can be constant in value and change in time (resistance force, pressure, etc.), applied for a short time (purse seine sampling with a non-salmon friction unit) and for a long time (trawling), in conditions of low (NEA, etc.), normal (ECA, etc.) or high (SEA, etc.) ambient temperature. The environment can create normal and higher pressure. In any case, the response of RSP and BC to loading will be in the form of elastic and plastic deformation or destruction [4]. The solid body, RSP and BC, has dimensions, shape and continuity. Two limit states are distinguished: one limit state is associated with loss of size and shape; the other with loss of continuity. Let's introduce the concept of continuity of RSP and BC – it is a characteristic that determines the ability of fibers of RSP and BC to fill the whole occupied volume without voids and defects, those fibers or threads, the volume of the rope-yarns, strands and the whole RSP and BC (Fig. 2).
а
b
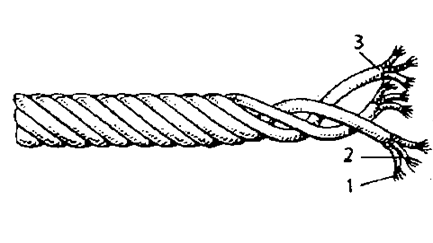
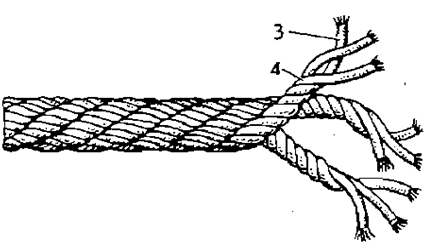
Fig. 2. Structure of the RSP and BC:
a – tether work tether; b – tether work cable:
1 – filaments and threads; 2 – rope-yarn; 3 – lock; 4 – strand
Structure of RSP and BC consists of winded fibers or threads 1 in a rope-yarn 2. From a few rope-yarns appears a strand 3, and several strands twisted together form a string, rope or tether. Tether work cable (see Fig. 2, b) is obtained by winding several tethers, which in the structure of such a tether are called strands 4. Determination of the continuity of the RSP and BC is performed using ultrasonic diagnostics (spectrometer): the beam passes through the entire product in the longitudinal and transverse direction at a certain angle. Measurement of the uniformity of the wave characteristics makes it possible to determine the presence and area of non-consolidation of RSP and BC – voids, delaminations and other defects.
Thus, the continuity class is the ratio of the cross-sectional area of the discontinuities (fibers) and the area of the RSP and BC, which is denoted by ,
![]() (1)
(1)
where nv is the number of fibers or threads in the section; Sv is the cross-sectional area of the fiber or thread; S is the cross-sectional area of the RSP and BC,
![]() , (2)
, (2)
where dv is the diameter of the fiber or thread,
![]() , (3)
, (3)
where d is the diameter of RSP and BC. Let us introduce assumptions: fibers, yarns, rope-yarns, locks, strands and the RSP and BC have a circular cross-section. The cross-sectional area of RSP and BC S is variable and depends on the load T, temperature and Poisson's ratio μ. The Young's modulus of RSP and BC E is variable and depends on load, temperature and Poisson's ratio μ. The influence of temperature on the fracture of RSP and BC is not considered in this article. We consider a uniaxial normal stress. The usual situation with a simple stress structure is observed in direct RSP and BC, which are subjected to tension under the action of oppositely directed forces along their axis (tension). Or (1) in the form considering (2) and (3)
![]() .
.
The continuity of RSP and BC is in the range0 ≤ Fo ≤ 1. The continuity is determined theoretically by the number of fiber or thread, string, rope or cord, by linear density, and with a spectrometer experimentally. When stretching anisotropic bodies, which are RSP and BC, their fibers get closer together in the cross section, thus the diameter d decreases. In this case the Poisson's ratio μ of anisotropic bodies depends on the continuity Fo:
![]() . (4)
. (4)
Note that Poisson's ratio μ for anisotropic bodies also depends on the change in the volume of RSP and BC V ≠ const, in which case we assume that Poisson's coefficient μ depends on the parameters
µ = f(ɛ, ɛd, Fo, v, θ, ξ, ζ),
where ε is relative elongation; εd is relative compression (expansion); ν is dimensionless volume; θ is dimensionless density; ξ is composite (heterogeneity);
ζ is twist (weave). Today the problem of reaching the limit state by the RSP and BC is considered empirically, as a rule [5, 6]. Experimental approaches for determining limit states are related to studies within the framework of the theoryof low-cycle fatigue in the fracture of materials, depending on their plastic properties and little on elastic constants. Any RSP and BC under load destroy and become either brittle (e.g. Dyneema RSP and BC) or ductile. To date, there is no theory that, for any type of stress, unambiguously establishes both the nature of failure and the value of ultimate stresses. The limit state criteria of material resistance are applicable to the evaluation of the bearing capacity of solids both in homogeneous and inhomogeneous stress fields. In the latter case, the loss of carrying capacity means the occurrence of the limit state in the local area in the vicinity of the most stressed point, which is called dangerous (e.g. in the rope trawls it is the eye splice of the rope ties). Nowadays, there are a large number of strength criteria, of which the classical ones are the most recognized. It is the classical strength hypotheses that are recommended in all modern Russian textbooks on strength of materials [7-9]. Let us dwell on some of them. The first criterion (the 1st strength theory (the theory of the greatest normal stresses): the cause of the onset of the limiting stress state is the greatest normal stresses). This criterion corresponds well to the experimental data obtained in tests of different RSP and BC under uniaxial tension [10]. It can be considered that at present this criterion is beyond doubt. The maximum stresses in the RSP and BC should not exceed the allowable stresses
![]() ,
,
where σmax – is the maximum tensile stress, σ > 1, N/m2; [σ] – is the limit (allowable) stress, N/m2.
The limiting (permissible) stress is defined by formula
![]() ,
,
where σo – dangerous stress, depends on material of RSP and BC, temperature, humidity, twist and other characteristics, it is defined experimentally; n – safety factor.
Experiments show that the strength of RSP and BC strongly depends on the structure defects, and the value of the limiting stress has a clear statistical character. Therefore, all the limit surfaces in the axes of principal stresses are a set of average statistical values of stresses, at which the RSP and BC pass into the fractured state instantly, if short-term strength is considered, or after
a guaranteed period of time, called durability, if we are talking about the long-term strength of the material.
Second criterion. In 1951, W. R. Regel [11] established the universal character of the time dependence of the strength in the form
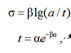
where α and β are material constants; t is durability, or the time during which processes occur in the loaded material, leading to its separation into parts (to brittle fracture).
Let us introduce assumptions:
– taking into account theoretical deductions [12] and neglecting the continuity Fo, composite (heterogeneous or mixed RSP and BC) ξ, twist (weaving) ζ, V = const and taking into account (4), we obtain
![]() ;
;
– the RSP and BC are regarded as perfectly flexible cylindrical products that are subject to longitudinal tension and compression, and transverse compression;
– the study of RSP and BC did not take into account design parameters such as the twist, the number of strands, the thickness of the wire and fiber, the type of weaving;
– the study of RSP and BC does not take into account the internal friction forces between the fibers and strands of RSP;
– velocity and acceleration of longitudinal stretching of RSP and BC are not taken into account;
– notional modulus in the cross section Ex = E = const;
– conditional modulus of elasticity along the surface Ey = const;
– volume of the RSP and BC under load does not change V = const;
– mass of the RSP and BC under the load does not change m = const;
– continuity in the process of loading does not change and is in the range of 0 ≤ Fo ≤ 1, it is true under the condition of constancy of the volume of RSP and BC V = const; breaking of RSP and BC fibers is compatible in time with the process of internal friction i.e. sliding of fibers against each other.
Problem statement
All commercial fishing gear have the synthetic fiber materials in their structure, which are produced from synthetic polymers. There are a large number of different types of synthetic fiber materials. In the construction and operation of industrial fishing gear, polyamide, polyester, polyethylene, polypropylene, polyvinyl chloride, polyvinylidene chloride, polyvinyl alcohol, and polyformaldehyde fibrous materials are mainly used. Polyamide fibers are obtained from synthetic high-molecular-weight polyamide resins. The starting material, mainly phenol, is commonly known as carbolic acid. These are some of the most common types of synthetic fibers, having a common international brand (designation) PA, but somewhat different depending on the properties of the starting materials, technology and peculiarities of production. Polyamide is obtained by polymerization from polycaprolactam. It is characterized by high strength, elasticity, chemical resistance, resilience, does not get wet, is not subject to rotting, is lightweight, has high spinning properties (Table 1).
Table 1
Technical properties of synthetic fiber materials
|
Material |
Density, kg/m3 |
Tensile strength, N/mm2 |
Loss in water, % |
Tensile elongation at break, % |
|
|
Dry fiber |
Wet fiber |
||||
|
Polyamide fibers |
|||||
|
Polyamide |
1 140 |
450-800 |
10-15 |
15-20 |
20-25 |
|
Nylon-16 |
1 140 |
500-700 |
10-15 |
16-22 |
20-27 |
|
Nylon-11 |
1 150 |
600-800 |
10-15 |
19-24 |
21-28 |
|
Anid |
1 150 |
600-800 |
10-15 |
19-24 |
21-28 |
|
Perlon |
1 150 |
400-700 |
10-15 |
16-22 |
20-27 |
|
Polyester fibers |
|||||
|
Lavsan |
1 380 |
550-800 |
0 |
|
|
|
Terylene |
1 380 |
500-800 |
0 |
19-23 |
10-23 |
|
Tetoron |
1 380 |
600-800 |
0 |
7-13 |
7-13 |
|
Polyvinyl alcohol fibers |
|||||
|
Vinylon |
1 300 |
400-700 |
20-25 |
17-25 |
20-30 |
|
Polyvinyl chloride and polyvinylidene chloride fibers |
|||||
|
Chlorine |
1 440 |
200-250 |
0 |
25-40 |
25-40 |
|
Saran |
1 700 |
200-300 |
0 |
18-30 |
18-30 |
|
Polypropylene fibers |
|||||
|
Polypropylene |
920 |
500-800 |
0 |
18-23 |
18-23 |
|
Polyethylene fibers |
|||||
|
Polyethylene |
950 |
300-500 |
0 |
10-23 |
10-23 |
|
Polyformaldehyde fibers |
|||||
|
Polyform |
1 200 |
500-800 |
0 |
13-15 |
13-15 |
Polyamide is used for the production of threads, netting, string and rope. Nylon is obtained from hexamethylenediamine and adipic acid. It has the same high spinning and technical properties (Table 1) as polyamide and is used for the same purposes. Polyester fibers are produced from ethylene glycol and trephthalic acid. There are different kinds of polyester fibers having common international brand PE but differing by initial materials, insignificant deviations in production technology, as well as by brand names. Imported terylene and teteron fibers are sometimes also used in fishery practice (Table 1). Polyethylene fibers are produced by polymerization from ethylene and are used less often than polyester or polyamide fibers. There are several varieties of polyethylene fibers, of which polyethylene is the most widely used. It is mainly used to make films, packaging and other insulating materials. It is also used for production of threads, nets and other fishing materials, though its technical properties are inferior to those of the materials described above (Table 1). It is especially widely used for the production of fishing line. Dyneema is the high molecular weight polyethylene material. Polypropylene fibres are produced from propylene and have a number of varieties with the common international brand PP, have high spinning and technical properties, are lighter and stronger than polyethylene, they are widely used for the manufacture of fishing rods (Table 1). Polyvinyl chloride and polyvinylidene chloride fibers are widely used in engineering, they include polyvinyl chloride, polyvinylidene chloride, saran and chlorine. Polyvinyl chloride is an artificial resin obtained by polymerization of vinyl chloride in the presence of organic peroxides. It is widely used in engineering for production of plastic masses. Polyvinylidene chloride is an artificial resin obtained by polymerization of vinylidene chloride in the presence of peroxides. International brand RUO. It is widely used in engineering for the production of plastic masses and textile fibers. Saran is a fiber produced from a mixture of polyvinyl chloride and polyvinylidene chloride (PVC + PVD). It is used for the production of fishing materials, has good spinning properties, but in some technical characteristics, such as strength, is inferior to kapron, nylon, etc. (Table 1). Chlorine is a fiber produced of polyvinylidene chloride. It is used for production of fishing materials, but is inferior to kapron, nylon, etc., according to its technical characteristics (Table 1). Polyvinyl alcohol fibers are produced from an aqueous solution of polyvinyl alcohol - a polymer obtained by hydrolysis of polyvinyl acetate. International brand PVA. They are called polyvinyl alcohol fibers and vinylone. They have good spinning properties, are strong, but lose their strength in water (Table 1). Polyform is a polyformaldehyde fiber with good spinning and very high technical qualities, it was started to use in production of threads and netting fabrics for the manufacture of trawls, purse seines and other fishing gear (Table 1). Elastic deformation disappears completely upon unloading. Plastic deformation is irreversible after unloading. Therefore, it is unacceptable in parts and elements of fishing gear, for example, in the dragropes, lines and rope links of the rope-net part of trawls, etc., due to the noticeable plastic deformations of RSP and BC. Fracture is a separation of RSP and BC or its fibers and strands. Fracture is also the limiting state of RSP and BC under load. To ensure the reliability of fishing gear and its elements, it is necessary to know the lowest values of stresses that cause unacceptable plastic deformation and fracture. These stresses are called limit stresses. And knowing the limit stresses at certain loading, it is necessary to be able to predict the limiting conditions in RSP and BC at any operational conditions. According to the nature of the deformation of the RSP and BC in the process of fracture, the fracture is divided into brittle and ductile. Fracture is called brittle if it occurs with a predominantly elastic deformation of the material of which the RSP and BC are made,
i.e. with stresses lower than the yield stress. As a rule, brittle fracture of RSP and BC is observed at low temperatures, at high rates of loading, at multicycle fatigue. Viscous fracture is called ductile fracture accompanied by the noticeable plastic deformations. This fracture mode is seen at high temperatures, high external pressure, some kinds of complex stress state and low-cycle fatigue. In any case, fracture is not an instantaneous critical event. Fracture is a process of damage accumulation that occurs in time and space. It ends in loss of carrying capacity due to the loss of continuity. Fracture is subdivided into localized and volumetric ones, according to the character of the process activation in space. Localized destruction is the development and propagation of one or more fiber fractures of RSP and BC. Volumetric destruction is a process of damage accumulation on the micro- and macrolevels uniformly in the whole volume of RSP and BC. Thus, volumetric fracture is a process of loosening the structure of the RSP and BC. The same RSP and BC under different conditions (temperature, pressure, loading rate, type of stress state, etc.) can become brittle in some cases and ductile in others. Therefore, brittleness and ductility are not properties of the material, but of a state. The division of structural materials into brittle and ductile ones, which exists in engineering terminology, is conditional and primarily reflects the physical and mechanical properties of these materials at low rates of loading under normal conditions (atmospheric pressure, room temperature). The main factors of external influence should include temperature, time, pressure, type of stress state, environment (contact with active chemicals, influence of bacteria). Deformation and strength properties of RSP and BC are also influenced by design and technological factors, such as size, filling, latexing, heat treatment, cohesion, twist, weave, compositing, mixed composition, etc. The influence of structural and technological factors is related to the RSP and BC structure, so the explanation of changes in physical and mechanical properties requires a physical approach (experimental studies). In engineering calculations, as a rule, the results of experimental studies of the effect of time (velocity) and tension are used. Elasticity is the ability after deformation (stretching) to restore its shape and size. The complete deformation of fibers consists of three stages: elastic, highly elastic and plastic. Elastic deformation disappears after ceasing of force; highly elastic deformation disappears gradually, and plastic deformation is irreversible. Elastic deformation is an important feature of fiber materials as it improves the performance of fishing gear. Excessive elastic deformation, however, is undesirable because it is counterproductive. The term ‘elasticity’ is used along with the term ‘resilience’ and describes the elastic deformation under low loads. Strength is the ability of fibers and products to resist tearing loads. Absolute strength is the greatest load a fiber or a product can withstand, it is measured in newtons (N). Tensile strength is the ratio of the absolute strength to the cross-sectional area of the fiber or a product and is expressed in N/mm2. Breaking length is the length at which the fiber breaks under the action of its own gravity. Numerically, it is equal to the ratio of the fiber texture to its absolute strength. Fatigue is a change in the technical properties of fibers, in particular strength, which occurs with alternating tension and removal of loads in the fibers. This process is accompanied by a loosening of the molecular structure and an increase in plastic strain. Stiffness is the ability to resist changes in shape. It is of secondary importance for fishing gears, but worsens the spinning properties of fibers. Insolation resistance is the ability of the fiber to retain strength when exposed to direct sunlight. This is especially important for synthetic materials which are resistant to water, especially sea water. Fishing gear work in water and their weakening effects can reduce the quality of products. Whether or not to account for volume changes at large deformations depends on the engineering problem. In most problems of plasticity theory, it is assumed that volume changes under plastic deformation can be neglected. In other problems, where physical nonlinearity is neglected, it is assumed that the change in volume during plastic deformation is constant and equal to the elastic change arising from a stress equal to the yield stress. However, in the problems of machine engineering and manufacturing of parts by pressing or cutting, in the problems of operation of machines and structures, evaluation of their strength and durability, neglecting physical nonlinearity and the change in volume can lead to a large error. The theories of plasticity idealize the complex behavior of real materials during plastic deformation. Moreover, hypotheses defining different models of plastic bodies are used for different materials and different applications. The simplest model of a plastic body is the model of an ideal, isotropic, incompressible rigid plastic body. This model is used to describe the behavior of materials whose uniaxial stress diagram has a yield point. For such materials, when the yield point is reached, there are developed the much larger plastic strains than elastic strains. In the ideal rigid plastic body model, the real uniaxial tension diagram is replaced by an idealized one consisting of two straight lines. In our case, we are dealing with anisotropic bodies, which are fishing materials. In the general case, the dangerous (limiting) stress state of RSP and BC of the fishing gear structure depends on the ratio between the three main stresses along the OX, OY and OZ axes. We consider the stress only along the OX axis. I.e. strictly speaking, for each ratio it is necessary to determine experimentally the value of the ultimate stress, which is unrealistic. Therefore, strength calculation methods have been adopted that would allow to estimate the hazard of any stress state from the equivalent stress occurring in equiprobable dangerous tension. They are called theories of strength (theories of ultimate stress states) [8]. Modeling the behavior of RSP and BC in different operational processes under large plastic deformations, taking into account the change in the geometry of RSP and BC, is one of the important tasks of mechanics
of industrial fishing tools. On the basis of Hooke's law [13], we have a relation that corresponds to the elasticity criterion, in our case, the elasticity criterion of RSP and BC
![]() ,
,
where T – is the longitudinal force of tension (stretching) of the RSP and BC, T = Tx; Tlx is the compensation force (opposing Tx) in the longitudinal direction (along the axis OX); E is the Young's modulus (elasticity) of RSP and BC, the elasticity module characterizing the ability of RSP and BC to resist deformation, that is, its rigidity, the more Е, the less deforms the material, Е = Еx; ε is the relative longitudinal deformation. And ES is the tensile stiffness of RSP and BC. Experimentally, according to the results of the RSP and BC tensile tests, the following dependences can be obtained (jerks are not produced):
– under the condition of not fixing S, stiffness
ES = f(T, ε)
ES = T / ε,
if S is fixed, elastic modulus E = f(T, S, ε)
E = T / εS, (5)
Based on the results of the experiments, the dependences at constant velocity v of the tearing machine volutes are constructed: ES = f(T, ε), E = f(Fo, T, S, ε) and σ = f(Fo, ε, E). The influence of twist, weave, number of strands, weaving technology will be referred to the factor cl. On the basis of calculated values of physical-mechanical characteristics (further PMC) of polyamide thread d = 0.45 mm up to the moment of thread break, graphs (see Fig. 3 and 4) of dependences μ = f(v, Тx) and σ = f(v, ε) were plotted.
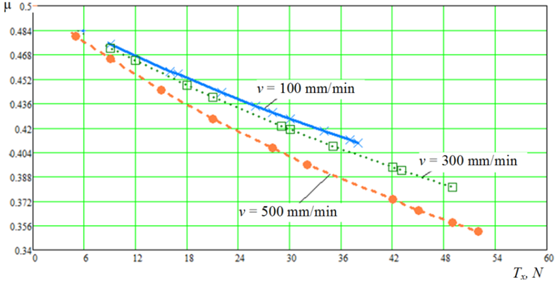
Fig. 3. Plots of the calculated values of PMC μ = f(v, Тx)
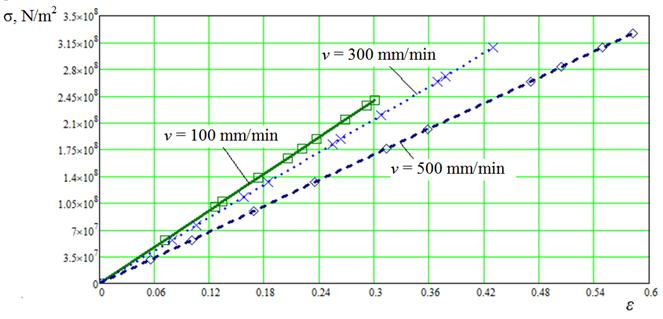
Fig. 4. Diagrams of calculated values of PMC σ = f(v, ε)
Based on the graphs of the dependencies μ = f(v, Тx) and σ = f(v, ε), we conclude: Poisson's ratio μ is not a material constant, but a function:
– poisson's ratio μ is not a material constant, but a function, most likely weakly dependent on temperature, pressure, type of stress state and strongly dependent on the kinetics of force impact; in engineering and scientific practice, the question of using Poisson's ratio or other formulas of transverse strain ratio in the mathematical model of the studied or considered process should be based on the accepted assumptions or provisions;
– the strength of net materials σ depends on the relative elongation of the material, the snail velocity v, the coefficient cl, which takes into account the influence of twist, weave, number of strands, weaving technology, as well as the modulus of longitudinal elasticity E:
![]() ,
,
where ρ is the weighted average density of the product.
Thus, E depends on [14]
![]() .
.
Consider an anisotropic body (RSP and BC) under the condition
![]() (6)
(6)
where vl – is the propagation velocity of the longitudinal wave in the CWI and SF.
Let us write down the equation
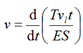 (7)
(7)
where t is the time of the stretching process of the synthetic material.
Solving equation (7) we obtain
![]() (8)
(8)
Then the relative elongation can be represented as
ε = v / vl.
Substituting expression (6) into (8), we obtain
![]() ,
,
or
![]() (9)
(9)
where c = cl2 is a coefficient proportionality.
Taking into account
![]() ,
,
it is possible to use the averaged values of the coefficient cl to calculate the PMC of network materials, while taking into account the structure of RSP and BC and for certain RSP and BC (Fo = const; ξ = const; ζ = const).
Let us write expression (9) as
![]() (10)
(10)
or in the form of the system
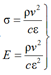 (11)
(11)
On the basis of experiments with polyamide thread d = 0.45 mm, let us determine the values of coefficients c and cl:
σ = T / S = ρv2/cɛ,
or
![]() .
.
The calculated PMC of a polyamide thread
d = 0.45 mm are given in Table 2.
Table 2
Calculated physical-mechanical properties of thread d = 0.45 mm, material – polyamide
|
Experimental PMC |
Calculated values coefficient c |
|||||||||
|
v, mm/min |
d, mm |
l, m |
S ∙ 10-7 m2 |
Tl, Tex |
ρ, kg/m3 |
Т, N |
ε, % |
с ∙ 10-10 |
|
k = 1/c ∙ 109 |
|
100.0 |
0.45 |
0.15 |
1.59 |
93.0 |
585.0 |
9.0 |
4.06 |
7.0 |
2.6 |
1.4 |
|
16.0 |
10.32 |
1.5 |
1.2 |
6.3 |
||||||
|
17.0 |
12.40 |
1.2 |
1.1 |
8.1 |
||||||
|
22.0 |
16.57 |
0.7 |
0.8 |
14.0 |
||||||
|
26.0 |
18.66 |
0.5 |
0.7 |
18.0 |
||||||
|
28.0 |
20.75 |
0.4 |
0.67 |
22.0 |
||||||
|
30.0 |
22.83 |
0.3 |
0.6 |
26.0 |
||||||
|
34.0 |
26.67 |
0.28 |
0.53 |
35.0 |
||||||
|
37.0 |
28.59 |
0.24 |
0.5 |
40.0 |
||||||
|
38.0 |
30.50 |
0.22 |
0.47 |
45.0 |
||||||
|
300.0 |
9.0 |
5.26 |
49.7 |
7.0 |
0.2 |
|||||
|
12.0 |
8.14 |
23.8 |
4.9 |
0.4 |
||||||
|
18.0 |
13.93 |
9.9 |
3.0 |
1.0 |
||||||
|
21.0 |
16.81 |
6.5 |
2.6 |
1.5 |
||||||
|
29.0 |
22.56 |
3.5 |
1.9 |
2.8 |
||||||
|
30.0 |
25.47 |
3.1 |
1.7 |
3.2 |
||||||
|
35.0 |
28.35 |
2.3 |
1.5 |
4.2 |
||||||
|
42.0 |
34.10 |
1.6 |
1.3 |
6.1 |
||||||
|
43.0 |
37.01 |
1.5 |
1.2 |
6.8 |
||||||
|
49.0 |
42.76 |
1.1 |
1.0 |
9.0 |
||||||
|
500.0 |
5.0 |
4.96 |
260.5 |
16.1 |
0.038 |
|||||
|
9.0 |
11.19 |
64.1 |
8.0 |
0.16 |
||||||
|
15.0 |
17.16 |
25.1 |
5.0 |
0.4 |
||||||
|
21.0 |
23.13 |
13.3 |
3.6 |
0.75 |
||||||
|
28.0 |
29.03 |
7.95 |
2.8 |
1.2 |
||||||
|
32.0 |
35.00 |
5.8 |
2.4 |
1.7 |
||||||
|
42.0 |
40.98 |
3.8 |
1.9 |
2.6 |
||||||
|
45.0 |
46.94 |
3.06 |
1.8 |
3.2 |
||||||
|
49.0 |
52.85 |
2.5 |
1.6 |
4.0 |
||||||
|
52.0 |
56.54 |
2.2 |
1.5 |
4.5 |
||||||
The tests were carried out according to GOST 6611.2-73 Textile threads. Methods of determination of breaking load and elongation at break.
Let us consider the RSP and BC as mechanical conservative systems [15]. This means that the work of an external force (tensile force) A is entirely spent on the communication of kinetic energy W and the accumulation of potential strain energy U:
A = W + U (12)
In order to calculate the potential energy, we assume that the external force is applied quite slowly. Therefore, in equality (12) we can neglect the kinetic energy
A = U .
Consider the deformation process of RSP and BC under uniaxial tension as a sequence of infinitesimal increments of rod elongation d△l caused by an increasing force T. Then the work produced by external force T in stretching of rod by △l will be calculated by formula
![]() (13)
(13)
where l is the length of the RSP and BC. Taking into account transformations, equality (13) will look like
![]() ,
,
V = lS is the volume of the RSP and BC Let σ and ε be related by the dependence σ = φ(ε). Then
U = uV
where u is the elastic energy per unit volume (specific potential energy),
![]() .
.
For an elastic body, which are RSP and BC, we obtain
![]() ,
,
or
![]() ,
,
and the cu coefficient is in the range (up to the tensile strength of the RSP and BC) of
![]()
for a linearly elastic body cu = 0.5.
If an external force is applied quickly (jerk), it is necessary to use the formula for calculating work (12). The jerk is a vector physical quantity that characterizes the rate (speed) of change in the body's acceleration. It is the third derivative in time of the radius-vector.
Results and discussion
Let us present the calculated data graphically
E = f(ε, v), E = f(k, v) and U = f(ε, v) of polyamide thread d = 0.45 mm before the thread rupture (Fig. 5-7).
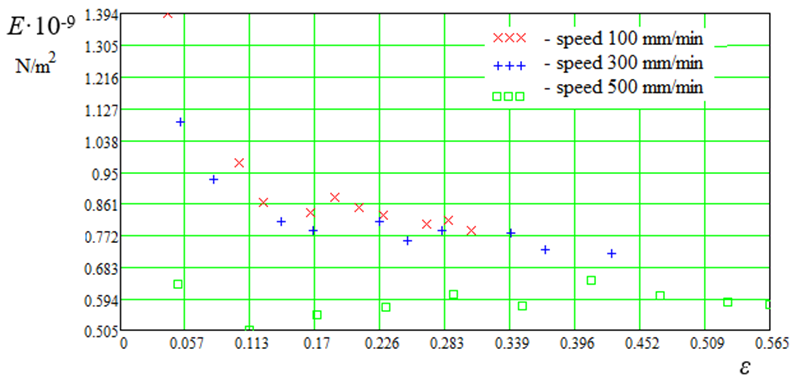
Fig. 5. Calculated data E = f(ε, v)
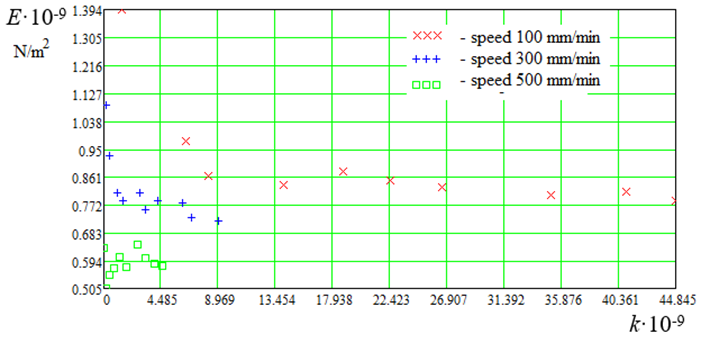
Fig. 6. Calculated data E = f(k, v)
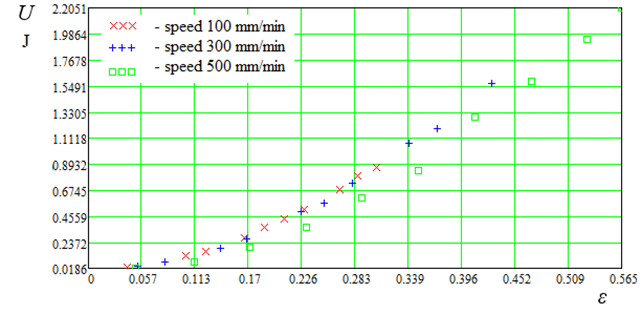
Fig. 7. Calculated data U = f(ε, v) at cu = 0.5
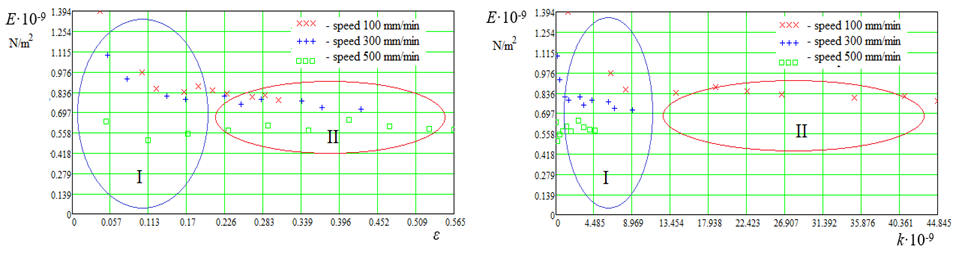
Fig. 8 (a, b) shows the calculated data E = f(ε, v) and E = f(k, v) and loading areas I and II, where it can be seen that in area I there is a strong change in E, while in area II there is no. This is due to the densification of the molecules in region I. The correction factor k corresponds to
k = 1/c .
a b
Fig. 8. Calculated data: a – E = f(ε, v); b – E = f(k, v); I, II – load area
Based on the graphs of the calculated data shown in Fig. 5-8 we can conclude that the loading theory of synthetic fishing materials needs to be developed and refined. It can also be noted that in the loading region I, compaction of synthetic fishing fibers molecules takes place. Calculated data (see Fig. 5), displayed graphically E = f(ε, v) are of interest from the point of view of longitudinal strain modulus E change depending on relative elongation ε. Comparison of Hooke's law (5) and expression (11) helps estimate the loading areas I and II of synthetic fishing materials.
Let's plot dependencies of the form k = f(ε, v), which are shown in Fig. 9
![]() , (14)
, (14)
under the condition
![]() ,
,
where b = 0.11 for v = 100 mm/min and v = 500 mm/min, and for v = 300 mm/min b = 0.18.
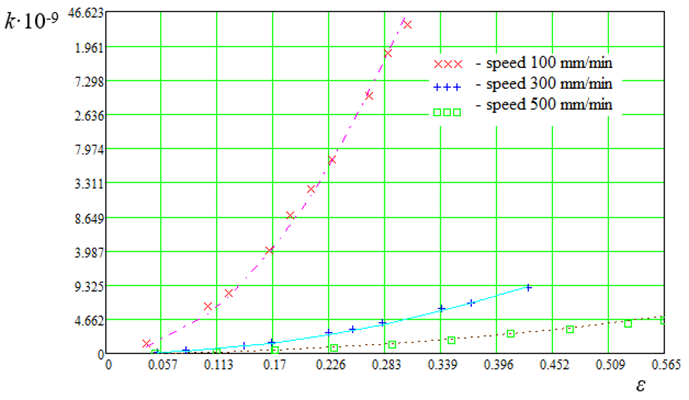
Fig. 9. Graphs of dependence k = f(ε, v)
Thus, according to (10) and (14), we obtain the relationship between the longitudinal modulus of elasticity E, the product density ρ and the strain rate v of synthetic fishing materials
![]() ;
;
![]() (15)
(15)
According to formula (15), we obtain the following values of longitudinal modulus of elasticity: E100 = 0.8 GPa; E300 = 0.72 GPa and E500 = 0.65 GPa.
Let's use expression (10) for calculating stress
![]()
The graph (Fig. 10) shows experimental and calculated data σ.
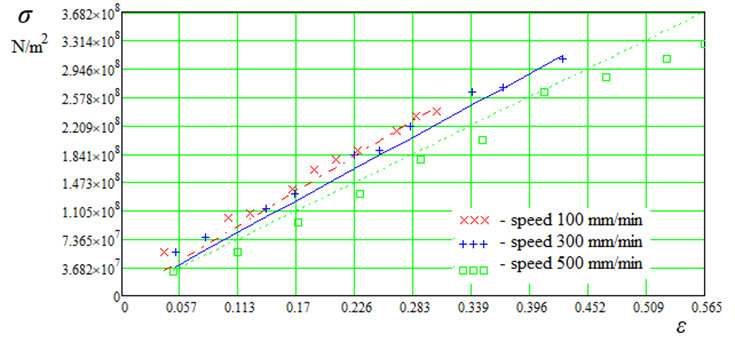
Fig. 10. Plots of dependence σ = f(ε, v)
Thus, the relationship between product density ρ, longitudinal elastic modulus E, relative elongation ε and strain rate v of synthetic fish traps is obtained. The problem of stress concentration reduction, which is obvious in connection with creation of new fishing trawls, purse seines and grippers of complex shape-changing geometry, is solved.
Conclusion
Expressions (11) characterize the theory of loading and fracture of the rope and string products, braided cords, etc. There have been made the conclusions about using Poisson's ratio μ in the theory of loading and fracture of RSP and BC, which is not a material constant but a function, most likely, weakly dependent on temperature, pressure, type of stress state and strongly dependent on the kinetics of force effect; in engineering and scientific practice the question of using Poisson's ratio or any formula of transverse strain ratio in the mathematical model of the studied or examined material is considered. The strength of network materials σ depends on the relative material stretching, the speed of movement of the stretching sections of RSP and BC v, the coefficient cl, which takes into account the influence of twist, weave, number of strands, weaving technology, as well as the modulus of longitudinal elasticity E. This work is a development of the theory of loading and fracture of synthetic fishing materials, the theory of strength of rope and string products and braided cords based on the principles of the solid-state physics. The totality of the theoretical and experimental data given and analyzed in the books testifies to the fact that the reliable data on the strength properties of RSP and BC can be obtained only on the basis of experiments and development of the physical theory of fracture and using the methods of statistical analysis. The universality of relations (11) is inherent in the very physical mechanism of loading and fracture of synthetic fishing materials.
All studies are aimed at the practical application of the safety factor of synthetic fishing materials, from which most of the tools of industrial fishing are made.
1. Sistema avtomatizirovannogo proektirovaniya orudiy promyshlennogo rybolovstva. URL: https://digitechlab.ru/cad-fg.html (data obrascheniya: 21.04.2022).
2. Nedostup A. A., Razhev A. O. Proizvoditel'nost' sil tralovoy sistemy: postanovka zadachi // Vestn. Astrahan. gos. tehn. un-ta. Ser.: Rybnoe hozyaystvo. 2021. № 2. S. 55-65.
3. Nedostup A. A., Razhev A. O., Nasenkov P. V., Konovalova K. V., Bykov A. A., Pivovarova Yu. S. Proizvoditel'nost' sil tralovoy sistemy - III: matematicheskoe modelirovanie (chast' I) // Vestn. Astrahan. gos. tehn. un-ta. Ser.: Rybnoe hozyaystvo. 2021. № 4. S. 63-72.
4. Birger I. A., Mavlyutov R. R. Soprotivlenie ma-terialov: ucheb. posobie. M.: Nauka, 1986. 560 s.
5. Baranov F. I. Teoriya i raschet orudiy rybolov-stva. M.: Pischepromizdat, 1948. 436 s.
6. Fridman A. L. Teoriya i proektirovanie orudiy promyshlennogo rybolovstva. M.: Leg. i pisch. prom-st', 1981. 327 s.
7. Bridzhmen P. V. Issledovanie bol'shih plasticheskih deformaciy i razryva. M.: Izd-vo inostr. lit., 1955. 444 s.
8. Kostenko N. A. i dr. Soprotivlenie materialov: ucheb. posobie. M.: Vyssh. shk., 2000. 430 s.
9. Pisarenko G. S. Soprotivlenie materialov. Kiev: Vyssh. shk., 1986. 775 s.
10. Nasenkov P. V., Nedostup A. A., Dolin G. M. Eksperimental'nye issledovaniya koefficienta Puassona nitevidnyh rybolovnyh materialov // Izv. Kali-ningr. gos. tehn. un-ta. 2021. № 62. S. 26-34.
11. Regel' V. R. O mehanizme hrupkogo razrusheniya plastmass // ZhTF. 1951. T. 21. Vyp. 3. S. 287-303.
12. Kachanov L. M. Osnovy teorii plastichnosti. M.: Nauka, 1969. 420 s.
13. Yavorskiy B. M., Detlaf A. A. Spravochnik po fizike. M.: Nauka, 1985. 258 s.
14. Nedostup A. A., Konovalova K. V., Nasenkov P. V., Razhev A. O., Al'tshul' A. B., Fedorov S. V. Otnositel'naya zhestkost' rybolovnyh kruchenyh izdeliy // Vestn. Astrahan. gos. tehn. un-ta. Ser.: Rybnoe hozyaystvo. 2020. № 1. S. 46-60.
15. Rabotnov Yu. N. Mehanika deformiruemogo tverdogo tela. M: Nauka, 1988. 712 s.