Russian Federation
Russian Federation
Russian Federation
The article considers the problem of planning the optimal loading of freight trains on a limited railway network – the network of a mining company. Two variants are illustrated. In the first variant only one type of locomotives operates on the railway network. In the second variant there are different types of locomotives. The types of lo-comotives are determined by their carrying capacity. The algorithm of scheduling multiple locomotives in a network is a combination of solutions for particular scheduling problems for each locomotive subject to the restrictions on their joint movement. Structurally, the set of possible locomotive schedules is a set of system states at discrete points in time. The state at each moment of time describes the location of each locomotive at a particular station and the amount of cargo transported. Thus, two consecutive states unambiguously determine the routes of locomotives. To describe a complete picture of all possible states and the sequence of their transitions from one state to another are represented in the form of a tree. There is proposed an algorithm for decreasing the variants of schedules by comparing the states in the tree nodes at each step and excluding the branches of states that would knowingly lead to a non-optimal schedule. The problem statement including several locomotives of different types, the solution algorithm and its application to a particular case are presented. In the formulation of the task the criterion of optimality for comparing different schedules is the minimum completion time of transporting the necessary volume of cargo. The additional criterion is total operating time of all locomotives, which is used only in case of equality of the main criterion for several schedules.
railway transport, schedule, locomotive, planning, order fulfillment, state, algorithm of gluing vertices
Введение
Функционирование железнодорожного транспорта горнодобывающих компаний непосредственно влияет на объем и непрерывность поставок полезных ископаемых. Сложность задачи оптимизации планирования загрузки железнодорожного транспорта зависит от размера железнодорожной сети, ее замкнутости, направлений перевозки грузов, наличия большого парка железнодорожного транспорта, необходимости перевозки различных типов материалов и пр. Инженерия управления в настоящее время является зрелой дисциплиной, однако она остается областью, в которой ведется большая исследовательская деятельность [1]. Оптимизация загрузки железнодорожного транспорта позволяет сократить издержки на перевозку грузов, создать резервы пропускной способности, доставлять грузы в установленные сроки, что повышает эффективность функционирования железнодорожной сети [2].
В отрасли железнодорожного планирования разрабатываются, внедряются и совершенствуются различные автоматизированные системы, например системы автоматизации диспетчерских центров управления перевозками, наращиваются возможности сети информационно-вычислительных центров [3]. Все это направлено на повышение эффективности использования парка железнодорожного транспорта, что влияет на объем и непрерывность поставок продукции. Задачи составления расписаний, решаемые в диспетчерских центрах, относят к категории NP-полных, для которых решение может быть получено полным перебором, но время, необходимое для этого, полиномиально зависит от объема исходных данных [4, 5]. Поэтому актуальным является поиск альтернативных методов решения задачи планирования работы железнодорожного транспорта, повышающих эффективность с точки зрения снижения трудоемкости, сокращения используемых вычислительных ресурсов.
В работе приведены две постановки задачи, первая включает проблему составления расписания для нескольких локомотивов одного типа, вторая – для локомотивов разных типов, а также алгоритм решения таких задач и его применение к частному случаю.
Постановка задачи с локомотивами одного типа
В работах [6, 7] представлены постановка задачи составления расписания и ее решение для случая, когда работу по перевозке грузов осуществляет один локомотив. В данной работе приведено развитие такой постановки задачи, в частности в этом пункте рассмотрен вариант составления расписания для нескольких локомотивов с одинаковыми характеристиками.
Введем следующие обозначения:
– h – номер локомотива, h = 1, …, m, где m – общее количество локомотивов; – n – общее количество станций; – 
–
– 
– 
Количество груза – заказы, которые необходимо перевезти с i-й станции в j-ю, появляются в определенные моменты времени на станциях отправления и не могут быть выполнены заранее. Необходимо составить расписание движения локомотивов, которое позволит обеспечить выполнение всех заказов. Расписание задается состоянием локомотивов в каждый момент времени.
Целевой функцией для данной постановки задачи является суммарное время выполнения заказов всеми локомотивами в момент завершения выполнения всех заказов:
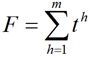(1)
Следует отметить, что в данном разделе рассматривается решение задачи с несколькими локомотивами одного типа. При этом состояние парка локомотивов перестает быть вектором [7] и становится матрицей, где h-я строка является состоянием h-го локомотива. В связи с тем, что рассматриваются локомотивы одного типа, будем считать состояния, включающие одинаковый набор строк, идентичными, как на рис. 1, и их также будем «склеивать».
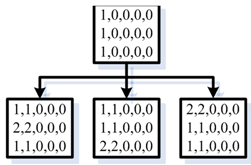
Рис. 1. Пример одинаковых состояний локомотивов
Fig. 1. Example of similar locomotive states
Здесь состояния имеют формат (s, t, k12, k13, k23).
В работе [6] представлен алгоритм склеивания вершин для решения задачи формирования составов и расписания их движения для одного локомотива. В настоящей работе представлено развитие этого алгоритма для случая с несколькими локомотивами одного типа, а также с несколькими локомотивами разных типов. Далее представлен сам алгоритм и пример его использования.
Алгоритм решения задачи планирования оптимальной загрузки нескольких локомотивов одного типа
Дерево состояний строится перебором различных вариантов движения локомотивов. В каждый момент времени с учетом ограничений [6] локомотив может находиться в одном из четырех состояний. Если локомотив перевозит заказ со станции отправления на станцию назначения, то он находится в состоянии «доставка». Если локомотив находится на станции, не выполняя никаких заказов, то он находится в состоянии «ожидание». Несколько ожиданий подряд допустимо. Если локомотив движется с одной станции на другую, при этом не перевозя грузов, то он находится в состоянии «холостой ход». Два и более холостых ходов подряд недопустимы. Если локомотив не функционирует, его состояние – «простой».
В результате перебора всех возможных состояний размерность дерева сильно увеличивается, поэтому для его уменьшения используется следующий алгоритм склеивания вершин.
1. Добавляем новое состояние в дерево и фиксируем его как матрицу Sj, каждая строка которой является состоянием отдельного локомотива.
2. Ищем среди построенных состояний такое,
у которого набор строк совпадает с набором строк матрицы Sj, а именно сравниваем их построчно. Таким образом, для любой k-й строки в матрице Sj существует аналогичная k-я строка в матрице Sj, . Если такое состояние не нашлось, переходим к п. 1, иначе к п. 3.
3. Находим родительское состояние Si–1 , предшествующее состоянию Si , и состояние Sj–1 предшествующее Sj. Сравниваем их, для этого считаем их значения состояний Si и Sj–1 по формуле
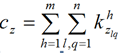(2)
где 𝑧 – номер состояния, равно (𝑖 − 1) или (𝑗 − 1); l – станция отправления; q – станция назначения.
Далее возможны два варианта.
3а. Если ci–1 > cj–1 , то прекращаем строить ветку, содержащую состояние Sj, , и удаляем ее. Переходим к п. 1.
3б. Если ci–1 < cj–1 , то удаляем ветку, содержащую состояние Si, до вершины Si включительно, а вершины следующих уровней переносим к состоянию Sj. Переходим к построению следующей ветки (п. 1).
Формула (2) представляет сумму выполненных заказов для заданного состояния. Будем считать более выгодным то расписание, в котором к заданному моменту времени выполнено больше заказов.
Пример решения задачи с тремя локомотивами одного типа для трех станций
Рассмотрим пример решения задачи построения расписания с тремя локомотивами одного типа для трех станций, расположенных по кругу. Используем обозначения, введенные выше. Схема расположения станций представлена на рис. 2.
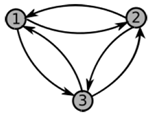
Рис. 2. Схема расположения станций
Fig. 2. Diagram defining the location of stations
Заказы отправляются со станций 1 и 2 и следуют на станции 2 и 3. Заданы три маршрута следования – со станции 1 на станцию 2 (его обозначим 12), со станции 1 на станцию 3 (13) и со станции 2 на станцию 3 (23). Новые заказы размером 1 условная единица появляются на станциях отправления в моменты времени 1 и 3, грузоподъемность локомотива равна 2 единицам. Требуется найти расписание, при котором все заказы будут выполнены за наименьшее время.
Построим дерево состояний для заданной постановки задачи, используя алгоритм склеивания вершин. Результат представлен на рис. 3.
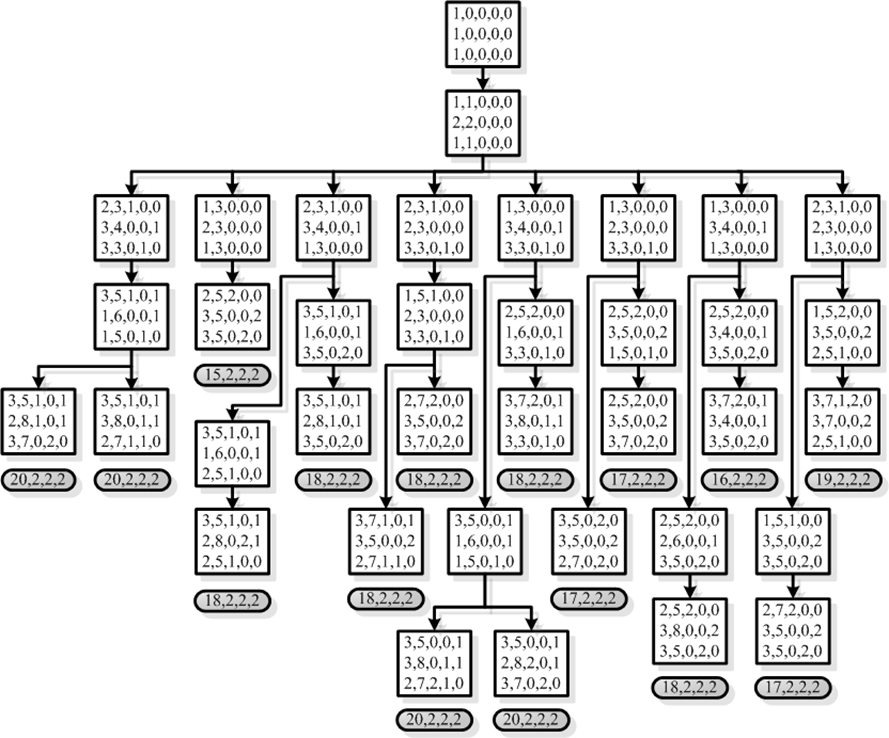
Рис. 3. Дерево состояний для трех локомотивов одного типа
Fig. 3. State tree for three locomotives of one type
Значение целевой функции вычислено по формуле (1) и представлено на рис. 3 после каждого расписания. Там же приведено количество доставленных заказов по каждому маршруту. Как видно из рис. 3, получено 16 возможных расписаний, при этом наименьшее значение критерия оптимальности равно 15 и достигнуто за счет ожидания заказов до полного заполнения локомотивов.
Постановка задачи с разными типами локомотивов
По сравнению с предыдущей постановкой, в случае, когда в задаче присутствуют локомотивы с разной грузоподъемностью, размерность задачи увеличивается и, как следствие, возрастает ее сложность.
Введем следующие обозначения: n – общее количество станций; L – количество типов локомотивов; m – общее количество локомотивов; hl – количество локомотивов типа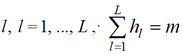 
– момент времени в расписании g-го локомотива типа l; 
– станция расположения g-го локомотива типа l; 
– количество доставленных локомотивом g типа l заказов с i-й станции отправления на j-ю станцию назначения, 
Кроме того, количество груза – заказы, которые необходимо перевезти с i-й станции в j-ю, появляются в определенные моменты времени на станциях отправления и не могут быть выполнены заранее. Необходимо составить расписание движения локомотивов, которое позволит обеспечить выполнение всех заказов.
Целевой функцией для данной постановки задачи является минимальное время завершения выполнения всех заказов среди максимальных в момент завершения выполнения всех заказов:
(3)
где 
– время завершения движения i-го локомотива, 
.
Для приведенной постановки задачи следует отметить, что в ней состояние транспортной системы в каждый момент времени описывается трехмерным массивом, каждый срез которого является состоянием локомотивов соответствующего типа и представляет собой матрицу. Кроме того, алгоритм построения дерева состояний аналогичен предыдущей постановке задачи, отличаясь большой размерностью из-за ограничений, приведенных в [6]. Для разработанного алгоритма поиска оптимального расписания предлагается следующая модификация алгоритма склеивания вершин.
Алгоритм склеивания вершин
В дерево добавляется новое состояние, которое фиксируется текущим 
Проводится проверка для всех состояний 
для любого локомотива g, 
и переходим на шаг 3. В случае отсутствия таких состояний осуществляется переход на шаг 1.
Проводится сравнение времен работы локомотивов при текущем и альтернативном состоянии.
Текущий маршрут удаляется и происходит возврат
к п. 1 (переход к другой ветке), если 
Удаляется маршрут, содержащий альтернативное состояние, если 
и происходит возврат к п. 1 (продолжается построение текущей ветки). В случае равенства времен 
отсев маршрутов происходит по суммарному времени работы всех локомотивов для состояний 
. Выбирается маршрут с наименьшим значением, другой удаляется.
В итоге получаем, что в случае совпадения состояний на отдельных этапах разных веток дерева маршрутов выбирается лучший вариант из условия минимума времени перевозки такого же и большего количества заказов.
Далее рассмотрим пример сокращения вариантов маршрутов на примере железнодорожной сети (см. рис. 1). Пусть в данной сети для перевозки грузов используются локомотивы двух различных типов. Различие определяется их грузоподъемностью: у локомотива первого типа она составляет одну единицу, а у второго – две. Также определены станции, откуда груз отправляется – 1 и 2, и станции, куда груз доставляется – 2 и 3. Маршруты перевозки в данной сети следующие: 12 (перевозка с первой станции во вторую), 13 и 23. На станциях отправления появление грузов происходит в моменты времени 1 и 3. Каждый заказ на перевозку равен одной единице груза. Ставится следующая задача: составить расписание перевозки всего объема груза, позволяющее минимизировать время завершения полной доставки.
Ниже приводятся примеры склеивания вершин в соответствии с описанным алгоритмом и получаемые готовые маршруты. Склеивание вершин отражено на рис. 4.
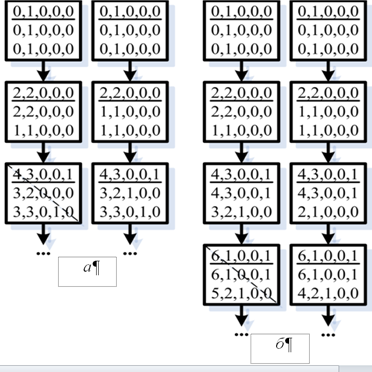
Рис. 4. Примеры склеивания вершин:
а – склеивание вершин, соответствующее случаю
перевозки разного количества груза
за одинаковое время;
б – склеивание вершин с одинаковым состоянием,
но достигнутым за равное время
Fig. 4. Examples of vertex gluing:
a – vertex gluing corresponding to the case
of transporting different amounts of cargo in equal time;
б – gluing vertices with the similar state,
but reached in equal time
Каждое состояние описывается набором данных следующего формата (t, s, k12, k13, k23)
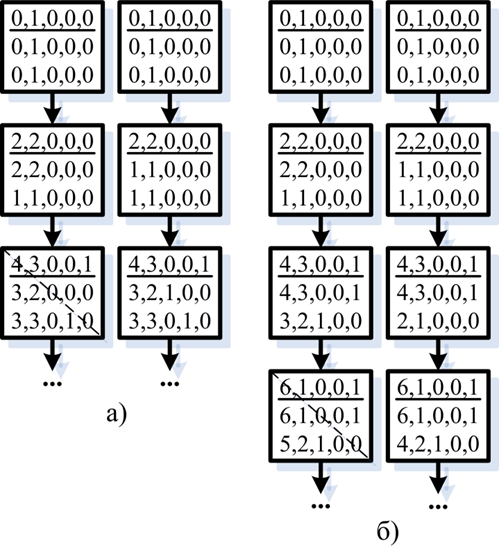
Рис. 5. Фрагмент дерева расписаний
Fig. 5. A fragment of a schedule tree
Для наглядности под каждым расписанием приводятся значения критерия оптимальности, вычисленного по формуле (3), и объем перевезенного груза по каждому из маршрутов. Минимальное значение критерия 7 достигается на нескольких расписаниях. В таком случае лучшим считается то, у которого меньше суммарное время работы локомотивов. Это расписание выделено на рисунке затененным прямоугольником. Всего в процессе сокращения вариантов были склеены 24 маршрута.
Заключение
В работе представлены два алгоритма планирования оптимальной загрузки железнодорожного транспорта – для однотипных локомотивов и для локомотивов разных типов. В таких постановках задачи состояние системы описывается в первом случае матрицей, каждая строчка которой соответствует отдельному локомотиву, а во втором случае трехмерным массивом, где матрицы описывают состояния локомотивов соответствующих типов. Добавление новых измерений в постановке задачи, таких как увеличение числа локомотивов и разделение локомотивов по характеристикам на различные типы, сильно увеличивает размерность задачи и усложняет решение перебором. Алгоритмы поиска оптимального расписания с применением процедуры «склеивания» состояний способны существенно сократить размерность дерева расписаний, что значительно облегчает процедуру поиска оптимального расписания. Представлен пример использования алгоритмов склеивания для решения частного случая описанной задачи. В дальнейшем планируется использовать предложенные алгоритмы в качестве основы для интеллектуальной системы планирования движения железнодорожного транспорта.
1. Baillieul J., Samad T. Encyclopedia of Systems and Control 2nd ed. 2021 Edition. Springer, 2021. PDF. 2497 p. 67 Mb. DOI: https://doi.org/10.1007/978-3-030-44184-5.
2. Matyuhin V. G., Shabunin A. B. Intellektual'nye sistemy upravleniya na zheleznodorozhnom transporte // Intellektual'nye sistemy upravleniya na zheleznodorozhnom transporte (ISUZhT-2014): tr. Tret'ey nauch.-tehn. konf. M.: OAO «NIIAS», 2014. S. 4-7.
3. Geiger M. J., Huber S., Langton S., Leschik M., Lin-dorf C., Tüshaus U. Multi-attribute assignment of trains to departures in rolling stock management // Annals of Operations Research. 2018. V. 271 (2). P. 1131-1163.
4. Cel'sova A. Yu., Hobotov E. N. Razrabotka metodiki formirovaniya marshrutov i raspisaniy dvizheniya gruzovyh poezdov po zheleznodorozhnoy seti // Intellektual'nye sistemy upravleniya na zheleznodorozhnom transporte (ISUZhT-2014): tr. Tret'ey nauch.-tehn. konf. M.: OAO «NIIAS», 2014. C. 11-14.
5. Lazarev A. A., Musatova E. G., Kvaracheliya A. G., Gafarov E. R. Teoriya raspisaniy. Zadachi upravleniya transportnymi sistemami. M.: Izd-vo MGU im. M. V. Lomonosova, 2012. S. 160.
6. Eletin E. V., Borovkova G. S., Galkin A. V. Formalizaciya zadachi zheleznodorozhnogo planirovaniya dlya gornodobyvayuschego predpriyatiya // Prikladnaya matematika i voprosy upravleniya. 2022. № 1. S. 37-51.
7. Eletin E. V., Borovkova G. S., Galkin A. V. Solving the Task of Forming Trains and Their Schedule for Four Stations Using the Algorithm of Vertex Gluing // 3rd Inter-national Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency (SUMMA) (Lipetsk, 10-12 November 2021). New Jersey: IEEE, 2021. Pp. 1013-1016.
