Russian Federation
Russian Federation
Russian Federation
The scientific and methodological base is being developed within the framework of systems theory and system analysis in application to the tasks of assessment, control and formation of dynamic states of technical objects, the design schemes of which are mechanical oscillatory systems with concentrated parameters. In the context of the fundamental problems of the theory of system studies of forced movements under deterministic disturbances there are considered the problems, whose solutions are aimed at developing a methodological approach to assessing the dynamic states of technical objects operating under coherent vibration loads. The purpose of the study is to develop a method for evaluating, controlling and forming dynamic states of the objects under harmonic force loads. It is assumed that mechanical oscillatory systems formed by a solid body performing small steady-state oscillations relative to the position of the static equilibrium can be used as calculation schemes of the technical objects. To construct mathematical models, Lagrange formalism, Laplace integral transformations taking into account zero conditions and structural methods are used, which make it possible to consider mechanical oscillatory systems as dynamically equivalent structural schemes of automatic control systems. The dynamic state of an object is assessed by using a transfer function, which in the physical sense represents the interpretation of a dynamic compliance. The amplitude-frequency characteristics used to assess the dynamic state of the object present a parametric family, for which the first parameter is the coefficient of connectivity of external force disturbances, and the second parameter is the coordinate of the point for which the dynamic accuracy is defined. An infinite family of amplitude-frequency characteristics is regularized due to the introduction of dynamic invariants, which can be considered as generalized dynamic states of mechanical oscillatory systems. To determine the dynamic invariants of a family of amplitude-frequency characteristics, taking into account two parameters, a map of dynamic invariants is constructed, which divides the plane of parameters into disjoint sets using boundaries. A theorem is proved to determine the explicit analytic expressions of these boundaries.
structural mathematical modeling, dynamic status, connectivity of force disturbances, resonance, dynamic damping of vibrations, dynamic compliance, map of dynamic invariants
Введение
Проблемы автоматизации технологических процессов, управления техническими объектами транспортного и технологического назначения, моделирования динамических взаимодействий элементов систем определяют широкий класс задач в таких отраслях технических наук, как машиноведение, динамика машин, прикладная механика, теория колебаний, вибрационная механика, теория автоматического управления, теория систем. К фундаментальным проблемам теории системных исследований могут быть отнесены изучение вынужденных движений механических систем и определение динамических состояний,
в которых система может находиться в зависимости от внутренних параметров самой системы и внешних возмущений [1]. Математические модели для широкого класса технических объектов могут быть построены на основе расчетных схем в виде механических колебательных систем с несколькими степенями свободы [2–5]. Для оценки движений в установившихся формах малых колебаний механических колебательных систем могут быть применены структурные методы математического моделирования [6, 7]. В рамках структурных подходов механические колебательные системы рассматриваются как эквивалентные в динамическом отношении структурные схемы систем автоматического управления [8]. Структурные методы находят свое применение в решении задач виброзащиты и виброизоляции [9, 10]. В плане практических приложений структурных подходов следует отметить задачи коррекции характеристик вибрационного поля рабочих органов вибрационных технологических машин [11].
В основе структурных методов лежат представления о типовых элементах, формах их соединений, структурных схемах и их эквивалентных преобразованиях [12]. Особое значение в плане применения системного подхода к исследованию механических колебательных систем как метода условного упрощения сложного объекта приобретает возможность приведения динамических характеристик, которое может быть выполнено в результате исключения части обобщенных координат из уравнений, характеризующих движение системы с несколькими степенями свободы. В частности, система с двумя степенями свободы может быть приведена к системе с одной степенью свободы путем исключения одной координаты. Динамические свойства системы с одной степенью свободы и динамические свойства системы с двумя степенями свободы, приведенной к одной координате, будут отличаться, но их структурные схемы могут рассматриваться как тождественные, т. к. формально образованы массоинерционным элементом, упругим элементом и внешним силовым возмущением, приложенным к массоинерционному элементу. Динамические свойства систем с одной степенью свободы и систем, приведенных к одной координате, могут быть определены на основе передаточных функций, в физическом смысле представляющих собой динамические податливости, равные отношению амплитуд смещения вынужденных установившихся колебаний к амплитудам силовых возмущений. Для системы с двумя степенями свободы дополнительное силовое возмущение, линейно связанное с исходным силовым возмущением, но приложенное ко второй точке, приводит к расширению разнообразия динамических свойств по сравнению с системой с одиночным силовым возмущением.
С целью разработки обобщенных подходов к оценке динамических состояний получила развитие концепция динамических инвариантов, в рамках которой амплитудно-частотным характеристикам передаточных функций ставятся в соответствие так называемые динамические инварианты в виде ориентированных графов, отображающих такие существенные динамические особенности, как количества резонансов, частот обнуления колебаний и количества знакоопределенных форм динамических взаимодействий элементов механических колебательных систем. В рамках концепции динамических инвариантов совокупность динамических состояний, отображаемая амплитудно-частотной характеристикой в зависимости от частоты внешних возмущений, может быть представлена набором из четырех показателей, обозначающих количественные характеристики динамических особенностей. Совокупность количественных показателей резонансов, частот обнуления и форм взаимодействий элементов системы может быть интерпретирована как обобщенное динамическое состояние системы.
В свою очередь, функциональная зависимость обобщенных динамических состояний от коэффициента связности, представленная в виде графика, может служить своеобразной интегральной характеристикой, демонстрирующей возможности изменения совокупности динамических свойств системы по мере варьирования параметра системы, в данном случае по мере изменения коэффициента связности. Наравне с коэффициентом связности в качестве вариационного параметра может быть рассмотрена координата точки, на основе которой оценивается с помощью передаточной функции динамическое состояние твердого тела. Для фиксированного значения коэффициента связности график зависимости обобщенных динамических состояний системы или характеристик динамических инвариантов, что то же самое, от координаты точки твердого тела представляет собой распределение динамических особенностей в виде числа резонансов, режимов динамического гашения и форм динамических взаимодействий по точкам твердого тела [13, 14].
В свою очередь, одновременная зависимость обобщенных динамических состояний от коэффициента связности и от координаты точки, на основе которой оценивается динамическое состояние твердого тела, позволяет построить так называемую карту динамических инвариантов. Карта динамических инвариантов позволяет для каждой пары параметров, образованной коэффициентом связности и координатой точки твердого тела, определять области, обладающие постоянными обобщенными динамическими состояниями. Карта динамических инвариантов представляет собой разбиения плоскости параметров на области, границы этих областей в виде линий и точки пересечения граничных линий.
Вместе с тем построение карты динамических инвариантов, множества которой отображают обобщенные динамические состояния механической колебательной системы в зависимости от коэффициента связности силовых возмущений и координаты точки, на основе которой оценивается динамическое состояние твердого тела, предполагает определение уравнений границ в явном виде, что еще не нашло достаточного уровня детализации представлений.
Предлагаемая статья посвящена задаче разработки метода определения параметрических областей, в которых сохраняют свои постоянные значения обобщенные динамические состояния механических колебательных систем в виде твердого тела, используемых в качестве расчетных схем технических объектов, находящихся в условиях вибрационных нагружений силовой природы.
Основные положения. Постановка задачи
Для рассмотрения предлагается механическая колебательная система, образованная твердым телом АВ. Твердое тело помещено на упругие опоры и совершает плоские движения в условиях связных гармонических синфазных возмущений Q1, Q2 силовой природы (рис. 1).
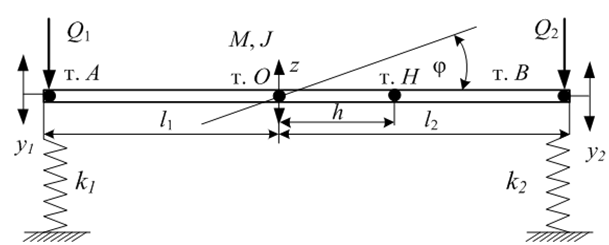
Рис. 1. Механическая колебательная система: АВ – твердое тело с массой M
и моментом инерции J; k1, k2 – жесткости упругих элементов; т. А, т. В – точки приложения силовых возмущений;
Q1, Q2 – силовые возмущения; т. О – центр тяжести; т. H – фиксированная точка;
z – вертикальные смещения центра тяжести; φ – угол поворота твердого тела;
y1, y2 – обобщенные координаты; l1, l2 – расстояния т. А и т. В от центра тяжести; h – координата т. H
Fig. 1. Mechanical oscillatory system: AB – rigid body with mass M
and moment of inertia J; k1, k2 – rigidities of the elastic elements;
p. A, p. B – points of forces excitations; Q1, Q2 – forces excitations; p. O – center of gravity; p. H – fixed point;
z – vertical displacements of the center of gravity; φ – angle of rotation of a rigid body;
y1, y2 – generalized coordinates; l1, l2 – distances of p. A, p. B from the center of gravity; h – the coordinate of p. H
Для силовых возмущений Q1, Q2 выполнено условие
Q2 = γ Q1,
где γ – коэффициент связности. Предполагается, что движения системы представляют собой малые вынужденные установившиеся колебания относительно положения статического равновесия.
Динамическое состояние твердого тела АВ оценивается на основе движений точки Н. На фиксированной частоте ω внешних возмущений точка
H совершает колебания с некоторой амплитудой. Для оценки динамического состояния твердого тела в точке H используется представление о динамической податливости в виде отношения амплитуд колебаний смещений к амплитудам колебания силовых возмущений Q1. Для различных значений частоты внешнего возмущения динамическая податливость может принимать положительные и отрицательные значения, а также отображать эффект резонанса или эффект обнуления амплитуды колебания.
Динамическое состояние системы определяется на основе особенностей движения точки Н с учетом текущего коэффициента связности внешних силовых возмущений; изменение коэффициента связности и координаты точки способны привести к существенной вариации совокупности динамических состояний, выражающейся в проявлении или устранении резонанса, проявлении или устранении режима обнуления, к смене форм динамических взаимодействий.
Оценивание особенностей динамических состояний может быть реализовано на основе карты динамических инвариантов, которая каждой паре, образованной значением коэффициента связности и координатой точки, ставит в соответствие характеристику обобщенного динамического состояния или, что то же самое, динамического инварианта.
Для построения карты динамических инвариантов может быть использована частотная функция обнуления амплитуды колебания точки H. Для фиксированных значений коэффициента связности и координаты точки H частотная функция обнуления позволяет определять частоты, на которых обнуляется числитель динамической податливости.
В свою очередь, равенство нулю частотной функции обнуления может быть рассмотрено как неявный способ задания критических или граничных значений параметров.
Вместе с тем условия совпадения частотной функции обнуления с частотами собственных колебаний механической системы еще не получило должного уровня детализации в плане определения свойств границ.
Задача заключается в определении существенных свойств границ множеств, образующих карту динамических инвариантов механической колебательной системы, образованной твердым телом, совершающим колебание в условиях связных возмущений, динамическое состояние которого оценивается на основе совокупности динамических податливостей точек, распределенных по всей поверхности твердого тела.
Математическая модель
Для построения математической модели в рамках формализма Лагранжа в качестве системы обобщенных координат может быть выбрана совокупность {y1, y2} смещений точек А и B твердого тела относительно положения статического равновесия или совокупность значений {φ, z}, где φ – угол поворота твердого тела, z – вертикальные смещения центра тяжести (см. рис. 1). Системы обобщенных координат {y1, y2} и {φ, z} связаны соотношениями
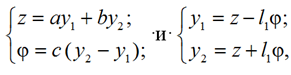
где 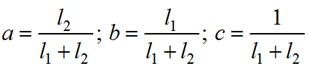
Для построения уравнений Лагранжа 2-го рода потенциальная и кинетическая энергии колебательной системы могут быть представлены в виде
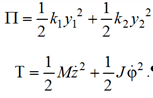
Приведенная к координатам {y1, y2} на основе известных методов [9, 10] механическая колебательная система (см. рис. 1) может быть представлена в виде структурной схемы (рис. 2), где p = jω – комплексная переменная; j = √–1; ω – частота внешнего возмущения; символ «–» над переменной обозначает интегральное преобразование Лапласа [15] с учетом нулевых начальных условий.
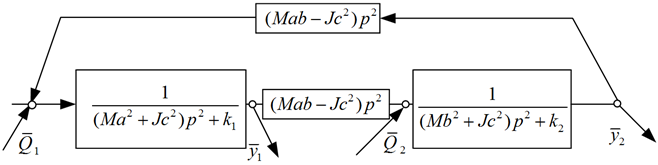
Рис. 2. Структурная схема механической колебательной системы
Fig. 2. Block diagram of a mechanical oscillatory system
По структурной схеме (см. рис. 2) на основе известных методов [8, 9] могут быть построены
передаточные функции системы:
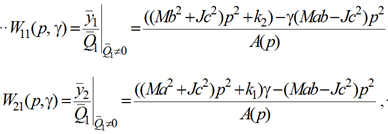 (1)
(1)
(2)
где A(p) = ((Ma2 + Jc2)p2+ k1)((Mb2 + Jc2)p2 + k2) – ((Mab – Jc2)p2)2 является характеристическим многочленом с корнями σ1, σ2, которые представляют собой собственные частоты системы (см. рис. 1).
Передаточные функции (1), (2) системы (см. рис. 1), построенные на основе структурной схемы (см. рис. 2), могут быть использованы для построения передаточной функции, для которой входным сигналом является гармоническое колебание внешнего силового возмущения, а выходным сигналом – колебание фиксированной точки твердого тела. В частности, для оценки динамических особенностей движений твердого тела в точке H (см. рис. 1) может быть использована передаточная функция
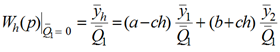 (3)
(3)
Многообразие динамических состояний точек твердого тела для фиксированного значения коэффициента связности γ может быть оценено на основе семейства амплитудно-частотных характеристик передаточных функций (3) с учетом координаты h:
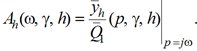 (4)
(4)
Существенные особенности амплитудно-частотных характеристик могут быть представлены в виде динамических инвариантов. Для оценки разнообразия динамических состояний, определяемых коэффициентом связности и координатой точки, на основе которой оценивается динамическое состояние объекта, может быть построена карта динамических инвариантов, представляющая собой совокупность множеств в виде областей, границ и их пересечений, на которых динамические инварианты остаются неизменными.
Определение форм границ карты динамических инвариантов
Карта динамических инвариантов может быть построена на основе границ, которые определяются с помощью частотной функции обнуления:
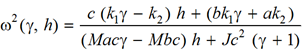 (5)
(5)
Частотная функция обнуления (5) ставит в соответствие параметрам системы частоту, в которой обнуляется числитель амплитудно-частотной характеристики (4). Особенности амплитудно-частотных характеристик могут поменяться при достижении частотной функцией (5) граничных значений, а именно, частотная функция обнуления может принять нулевое значение, принять критическое бесконечно большое значение, может совпасть с первой собственной частотой или со второй собственной частотой. Так как в системе существует два параметра, то каждому коэффициенту связности γ можно поставить в соответствие значения координат точек h0(γ), hkp(γ), h1(γ), h2(γ),
в которых частотная функция обнуляется, достигает критического значения, совпадает с первой или со второй собственной частотой соответственно. Границы областей карты динамических инвариантов могут быть определены с помощью функций h0(γ), hkp(γ), h1(γ), h2(γ) независимой переменной γ:
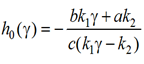
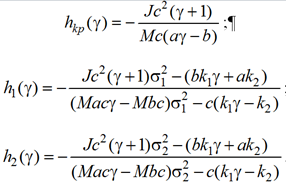
Взаимное расположение графиков функций h0(γ), hkp(γ), h1(γ), h2(γ) на декартовой плоскости
с осями γ и h позволяет построить карту динамических инвариантов. Необходимо отметить, что функции h1(γ), h2(γ), рассматриваемые как функции независимого переменного γ, представляют собой константы. Докажем это.
Теорема. Пусть ω2(γ, h) – частотная функция обнуления системы, σ1, σ2 – собственные частоты системы, тогда границы h1(γ), h2(γ) карты динамических инвариантов, определяемые условиями ω2(γ, hi(γ)) = σi2, i = 1, 2, являются постоянными функциями независимой переменной γ.
Доказательство. Собственные частоты σi,
i = 1, 2, системы могут быть найдены из условия равенства определителя системы нулю с учетом подстановки pi = jσi:
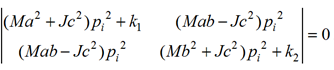 (6)
(6)
Равенство (6) означает, что столбцы матрицы, полученной после подстановки pi = jσi, i = 1, 2,
в систему (6), линейно зависимы. Не ограничивая общности, можно полагать, что существуют такие λi, i = 1, 2, что выполнено условие линейной зависимости в форме
![]() (7)
(7)
![]() (8)
(8)
В свою очередь, структура передаточной функции Wh(p) на основе формул Крамера может быть представлена в виде
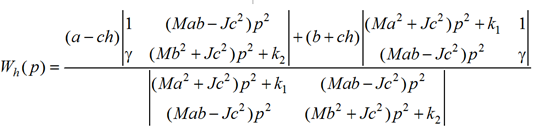 (9)
(9)
Частотная функция обнуления ω2(γ, h) может быть определена в неявной форме, путем приравнивания числителя передаточной функции (9)
к нулю:
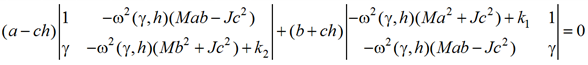 (10)
(10)
При условии, что ω2(γ, hi(γ)) = σi2, i = 1, 2, функции границ h1(γ), h2(γ), выраженные из
условий (10), принимают явный вид:
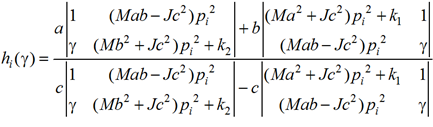 (11)
(11)
Учитывая линейную зависимость столбцов (7),
(8), запишем (11) в виде
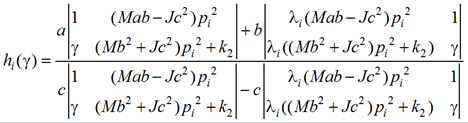 (12)
(12)
Используя свойства определителей, числитель и знаменатель выражения (12) может быть сокращен на множитель
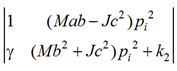 (13)
(13)
После сокращения на множитель (13) выражение (12) принимает вид
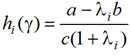 (14)
(14)
Выражение (14) определяется геометрическими характеристиками твердого тела и не зависит от особенностей приложения внешних возмущений, следовательно, граница hi(γ) является постоянной функцией переменной γ. Теорема доказана.
Таким образом, для построения карты динамических инвариантов необходимо учитывать, что границы, определяемые условиями совпадения частотной функции обнуления с собственными частотами системы, представляют собой прямые линии.
Заключение
В рамках фундаментальных проблем теории системных исследований вынужденных движений технических объектов рассмотрена задача оценки разнообразия динамических состояний механических колебательных систем, образованных твердыми телами, находящимися в условиях связных возмущений силовой природы. Для оценки разнообразия динамических состояний механических колебательных систем разработан обобщенный подход, использующий понятие динамического инварианта, отображающего существенные особенности динамических состояний в виде числа резонансов, числа режимов динамического гашения колебаний и числа знакоопределенных форм, приходящихся на множество вынужденных динамических состояний, определяемых всевозможными частотами внешних гармонических силовых возмущений.
Показано, что разнообразие динамических состояний семейства систем, зависящего от двух параметров в виде коэффициентов связности и координат точки, используемых для оценки динамических состояний, может быть отображено на плоскости
с помощью совокупности множеств, образующих так называемую карту динамических инвариантов.
Уставлено, что карта динамических инвариантов определяется граничными линиями, удовлетворяющими аналитическим уравнениям, полученным на основе сравнения частотной функции обнуления колебаний с критическими значениями, включающими в свой состав собственные частоты колебаний системы. Доказано, что граничные линии, уравнения которых определены из условий совпадения частотной функции обнуления с собственными частотами, представляют собой постоянные функции коэффициента связности внешних возмущений.
Таким образом, разработана теоретическая основа для анализа структуры обобщенных динамических состояний технических объектов, находящихся в условиях вибрационных нагружений силовой природы, расчетные схемы которых могут быть представлены параметрическими семействами механических колебательных систем.
1. Kalinin V. N. Four fundamental problems of the theory of system research // Proceedings of the Military Space Academy named after A. F. Mozhaisky. 2012. N. 637-2. P. 62-73.
2. Harris S. M., Cred C. E. Shock and Vibration Hand-book. N.Y.: McGraw-Hill Book Co, 2002. 1457 p.
3. Clarence W. de Silva. Vibration. Fundamentals and Practice. Boca Raton: CRC Press, 2006. 1064 p.
4. Tarasik V. P. Mathematical modeling of technical systems. Minsk: DesignPro, 2004. 640 p.
5. Rynkevich S. A. New technologies and problems of science in transport. Mogilev: Belarusian-Russian University, 2009. 337 p.
6. Kolovsky M. Z. Automatic control of vibration protection systems. M.: Nauka, 1976. 320 p.
7. Eliseev S. V. Applied system analysis and structural mathematical modeling (dynamics of transport and techno-logical machines: connectivity of movements, vibration interactions, lever connections): monograph. Irkutsk: IrGUPS, 2018. 692 p.
8. Eliseev S. V. Structural theory of vibration protection systems. Novosibirsk: Nauka, 1978. 212 p.
9. Eliseev S. V., Reznik Yu. N., Khomenko A. P., Zasyadko A. A. Dynamic synthesis in generalized problems of vibration protection and vibration isolation of technical objects. Irkutsk: IGU Publishing House, 2008. 523 p.
10. Karnovsky I. A., Lebed E. Theory of Vibration Protection. Springer International Publishing, Switzerland, 2016. P. 708.
11. Eliseev A. V., Aryunin A. I., Nguyen D. H., Vyong K. C. Control of the vibration field of a technological machine based on changes in the reduced inertial properties // Vibration technologies, mechatronics and controlled machines: collection of scientific articles: in 2 hours. Kursk: South-West State University, 2016. Part 1. 343 p.
12. Eliseev A. V., Mironov A. S., Eliseev S. V. System approaches in assessing mechanical oscillatory system dynamics: technology of structural transformations // Vestnik of Astrakhan State Technical University. Series: Management, Computer Science and Informatics. 2022. N. 1. P. 7-15.
13. Eliseev A. V., Sitov I. S., Kuznetsov N. K. System approaches to the assessment of dynamic states of technical objects under vibration loads: frequency functions, dynamic invariants, regularization methods // Systems. Methods. Technologies. 2022. N. 4 (56). P. 7-15.
14. Eliseev A. V., Mironov A. S. Evaluation of dynamic features of technical objects under conditions of coherent vibration loads based on a map of dynamic invariants // Computer-aided design in mechanical engineering: Materials of the X International Scientific and Practical Conference. Saint-Petersburg: SIC MS, 2022. N. 13. P. 96-105.
15. Lurie A. I. Operational calculus and application in technical applications. M.: Nauka, 1959. 368 p.















