Введение

Освоение оптического диапазона электромагнитного спектра и создание оптоэлектрических машин и устройств является парадигмой научно-технического прогресса XXI в. В работах [1, 2] приведена возможность передачи динамическим электротехническим комплексам (ДЭК) одновременно информации и энергии по лазерному лучу. Современные технологии фотоэлектронных преобразователей (ФЭП), основанные на внутреннем фотоэффекте в тонких полупроводниковых слоях, позволяют реализовать высокую эффективность (в лабораторных условиях КПД ФЭП достигает 70 %) [3]. При использовании ФЭП удается, например, запускать маломощные электродвигатели [4, 5]. Однако применение многослойных ФЭП ограничено невысокой лучевой прочностью, и для достижения более значимых уровней электрической мощности требуется объединение большого количества маломощных преобразователей в батареи, например солнечные.

В последние годы альтернативным направлением доставки по лазерному лучу электроэнергии к ДЭК рассматривается генерация мощных импульсов тока и магнитных полей по методу «конденсатор-катушка» (КК) [6–9]. Конденсатор образуют два сближенных торца индуктивной катушки. Через отверстие в одном из торцов излучение фокусируется на поверхности второго торца-мишени. При интенсивности излучения свыше 10¹⁰ Вт/см² происходит ионизация поверхностного слоя материала мишени, выход из нее горячих электронов, образующих приповерхностную плазму (ППП) внутри конденсатора. Под действием сторонних сил неэлектрической природы заряды в плазме разделяются и возникает электродвижущая сила (ЭДС), поддерживающая за время длительности оптического импульса поток носителей заряда через катушку. Разрядный ток конденсатора генерирует в катушке индуктивности мощное импульсное магнитное поле.

Исследование нелинейных процессов, происходящих в ППП, позволит оптимизировать работу динамических оптоэлектрических комплексов с оптической доставкой электроэнергии.

В настоящей работе приведены результаты теоретических и экспериментальных исследований пространственно-энергетических характеристик лазерной плазмы, возбуждаемой внутри конденсатора при генерации тока и магнитного поля КК-методом, в зависимости от расходимости лазерного излучения. Рассмотрена возможность применения КК-преобразователя лазерного излучения в ток обмотки якоря бесколлекторного электродвигателя.

Методы и материалы исследования

1. Модель «конденсатор-катушка». Современные лазерные системы на кристалле титан-сапфира с пассивной синхронизацией мод могут генерировать интенсивные ультракороткие лазерные импульсы на длине волны около 800 нм [10]. Создаются установки с импульсной энергией от миллиджоулей до джоулей и длительностью в десятки фемтосекунд, с пиковой мощностью порядка тераваттна, частотах повторения импульсов порядка килогерц [11]. Подобные установки могут быть компактны, что делает их перспективными для различных применений, в частности в электродвигателях электротранспорта [12, 13]. В целях развития работ по направлению «Оптоэлектронные средства передачи информации и энергии» [1–5] (по договору о сотрудничестве между Государственным университетом морского и речного флота им. адмирала С. О. Макарова и Научно-производственным объединением Государственного оптического института им. С. И. Вавилова) проведены совместные теоретические и экспериментальные исследования оптической генерации тока и магнитного поля КК-методом.

Сущность метода иллюстрирует модельная схема (рис. 1) [7, 8].

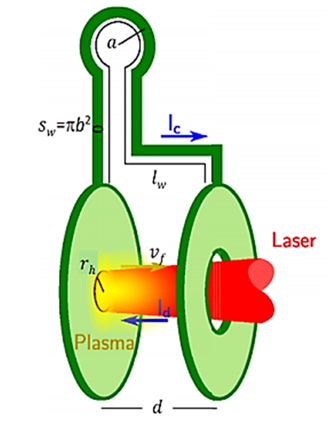
Рис. 1. Схема «конденсатор-катушка»: конденсатор образован двумя параллельными пластинами,
расположенными друг от друга на расстоянии d, правая пластина снабжена отверстием для прохождения
мощного импульса лазерного излучения внутрь конденсатора; катушка представлена одним витком
радиуса a, длиной l_w, площадью поперечного сечения провода s_w = πb², где b – радиус поперечного сечения провода

Fig. 1. “Capacitor-coil” scheme: the capacitor is formed by two parallel plates located at a distance d from each other. The right plate has a hole for passing a powerful laser radiation pulse into the capacitor; the coil has one winding with radius a, length l_w, wire cross-sectional area s_w = πb², where b – a wire cross-sectional radius

Об адаптации модели «конденсатор-катушка» для лазера с длиной волны 1,06 мкм сообщалось в работе [6]. Авторы использовали лазер «Вулкан» с энергией импульса 300 Дж, интенсивностью излучения 4 · 10¹⁶ Вт/cм² и длительностью 1 пс и получили магнитное поле до 28 Tл в медной петле диаметром 2 мм. Обнаруженное магнитное поле представляло импульс длительностью порядка наносекунд. Авторы работы [7] сообщили, что с 1 кДж импульсом лазера Gekko, работающего на длинах волн 1,06 и 0,53 мкм, и катушек с миллиметровым диаметром получены магнитные поля, превышающие 1,5 кTл. То есть увеличив лазерную энергию в 3 раза, они получили усиление магнитного поля в 50 раз по сравнению с результатами работы [6].

2. Горячие электроны в лазерной плазме. В исходном состоянии в отсутствие импульса лазерного излучения (ЛИ) конденсатор заполнен вакуумом (рис. 1). При взаимодействии с пластиной-мишенью ЛИ, прошедшего через отверстие в другой пластине конденсатора, поверхностный слой мишени в зоне фокального лазерного пятна ионизируется в результате резонансного поглощения излучения. Возле облученной пластины внутри конденсатора возникает квазинейтральная лазерная плазма, возбужденная горячими электронами и ионами. Напряжение на конденсаторе достигает максимального значения u_c = E_c, ток в катушке I_к = 0 A. Через промежуток времени τ_d после подачи импульса ЛИ расширяющаяся плазма достигает пластины с отверстием, в плазме происходит разделение зарядов, она становится проводящей. Начинается разряд конденсатора через катушку, причем электрическое сопротивление конденсатора на порядки превышает малое сопротивление катушки, заряженный конденсатор работает как источник тока. Импульс тока в катушке генерирует интенсивное магнитное поле.

Уравнение внешней КК-цепи после коммутации может быть представлено в виде

                                                                              u_c = ri + L(di / dt),                                                                 (1)

где u_c – напряжение на конденсаторе; r – сопротивление; L – индуктивность катушки; i – ток в катушке. Оценка величины напряжения на конденсаторе u_c может быть получена при выражении заряда конденсатора Q_c через плотность горячих электронов n_h и функцию их распределения f_h(ε), которая зависит от энергии электронов:

Q_c = eπr_h²n_hΔΩ∫_(eUc)f_h(ε)dε,

где r_h – радиус зоны эмиссии, соответствующий радиусу лазерного пятна; ΔΩ – телесный угол эмиссии горячих электронов; ε – энергия электронов. Напряжение на конденсаторе:

                                                                             u_c(t) = C^–1∫^tQ_c(t')dt'.                                                              (2)

Для вычисления тока в цепи катушки подставляем u_c(t) из (2) в (1). Напряжение u_c не зависит от тока в цепи катушки и определяется внутренними процессами в конденсаторе. Предполагая максвелловское распределение горячих электронов с температурой T_h и вылет электронов в телесный угол ΔΩ ∼ π, а также заменяя временное интегрирование в (2) умножением на длительность лазерного импульса t_и, можно оценить напряжение на конденсаторе:

u_c ≈ e^–1T_hln[(ω_ph²t_иd / v_h)(r_h² / S_d)],

где ω_ph = (e²n_h0 / ε₀m_e)^1/2 – плазменная частота горячих электронов с плотностью n_h, тепловой скоростью v_h = (T_h / m_e)^1/2. Аргумент логарифма может достичь значения 10⁶, что соответствует напряжению в 15–20 раз больше, чем температура горячих электронов T_h. При средней электронной температуре 15–20 кэВ напряжение может составить 200–300 кВ в соответствии с экспериментальными данными [6].

Согласно численному моделированию [8] и экспериментальным измерениям [9], температура горячих электронов, кэВ, определяется как

                                                                              T_h ≈ 12(I_lasλ²_las)^0,42.                                                            (3)

Здесь интенсивность излучения лазера I_las  выражается в ПВт/см², длина волны лазера λ_las – в микронах (мкм). Соответствующую плотность горячих электронов можно оценить, предположив выполнение баланса мощности: hl_las ≈ n_h0v_hT_h,   где  v_h = (T_h / m_e)^1/2 – средняя скорость горячих электронов; h  – доля лазерной энергии, переданная электронам. По оценкам [10], она колеблется в пределах от 0,01 до 0,1.

Тогда

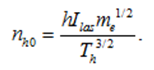
                                                                                           (4)

Уравнение (1) имеет решение: 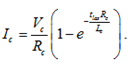. Магнитное поле в контуре можно выразить с учетом (3), (4) непосредственно через лазерные параметры:

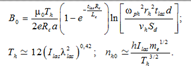
                                                            (5)

Формулы (5) позволяют оптимизировать значения тока I_c и магнитного поля как функций интенсивности I_las ЛИ и длительности лазерного импульса t_и = t_las.

Оценивая сопротивление конденсатора , можно получить довольно большое значение:

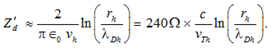
Проанализировав рис. 2, можно заключить, что электрическое поле в конденсаторе меняет знак и ускоренные в зоне планарного расширения ионы тормозятся в транспортной зоне. 

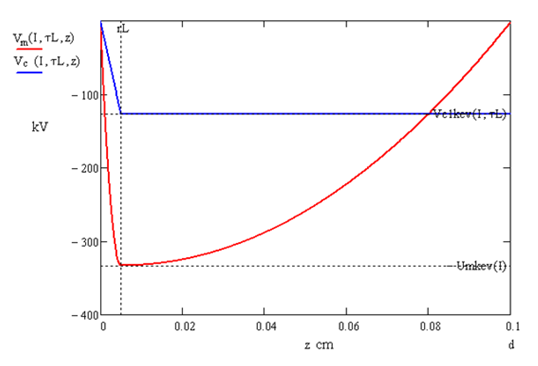
Рис. 2. Количественный расчет распределения потенциала в конденсаторе: стационарное распределение при Z_f  ≈ r_h  (вертикальная пунктирная линия) представлено сплошной синей линией; переходное распределение
до потенциального уравновешивания (конденсаторный потенциальный барьер) – красной линией; интенсивность лазерного излучения – 10¹⁶ Вт/см²; длительность лазерного импульса – 1 нс; емкость конденсатора – 0,1 пФ;
индуктивность – 5 нГн

Fig. 2. Quantitative calculation of the potential distribution in the capacitor: stationary distribution at Z_f  ≈ r_h  (vertical dotted line) – solid blue line; transitional distribution before potential balancing (capacitor potential barrier) – red line; radiation
intensity - 10¹⁶ W/cm²; laser pulse duration - 1 ns; condenser capacity - 0.1 pF; inductance - 5 nH

 Очевидно, что сопротивление конденсатора на два-три порядка больше, чем сопротивление внешней цепи, а ток в конденсаторе сильно ограничен его внутренним сопротивлением.

Электрическое поле в конденсаторе меняет знак, и ионы, ускоренные в зоне планарного расширения, тормозятся в транспортной зоне. Падение потенциала в зоне ускорения плазмы связано с наличием пологой характеристики в транспортной зоне. Такое распределение потенциала согласуется с общей теорией конденсатора с плазменным заполнением, первоначально предложенной Пирсом [11] и далее развитой в [12–14]. Электрический ток, который пройдет через этот потенциальный барьер, можно оценить как

где    определяет максимальный ток, который может быть извлечен из конденсатора. Согласно распределению горячих электронов (5) это значение может составлять 10 MA и более. Однако ток во внешней цепи намного меньше, он зависит от длительности лазерного импульса и сопротивления внешней цепи Z_c. Вольт-амперная характеристика конденсатора определяется условием непрерывности тока I_d = I_c,  где

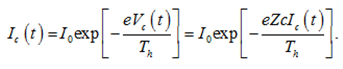
                                                         (6)

 Для оценки тока конденсатора можно заменить напряжение во внешней цепи упрощенным соотношением   Решая затем уравнение (6) в пределе 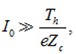 находим ток

 и соответствующее ему магнитное поле

Безразмерный параметр, контролирующий ток конденсатора, равен eZ_cI₀ / T_h.  Он может быть порядка 10²–10³. Для температуры горячих электронов T_h ~ 30–40 кэВ  и Z_c = 1 Ом напряжение в конденсаторе может быть 7T_h / e ≈ 200 кВ  и ток 200 кА. Эта оценка свидетельствует о возможности генерировать достаточно большие токи в конденсаторе, заполненном разреженной плазмой.

Лазерная коммутация КК-цепи

При направлении мощного импульса ЛИ на левую пластину-мишень через отверстие в другой пластине конденсатора (см. рис. 1) происходит ионизация поверхностного слоя материала мишени в области лазерного пятна и выброс горячих электронов в направлении навстречу лазерному лучу. Мишень, теряющая электроны, становится положительно заряженной пластиной конденсатора. Ток в катушке остается равным нулю, поскольку он не может измениться скачком в соответствии с первым законом коммутации, а внутри конденсатора образована квазинейтральная плазма. Конденсатор заряжается до максимального напряжения u_c = E_c не мгновенно, а за переходное время, согласно второму закону коммутации, с постоянной времени τ_с = Х_сC, где Х_с – сопротивление; C – емкость конденсатора. По мере заряда конденсатора в нем возникает электрическое поле, препятствующее переносу носителей заряда под действием сторонних сил. Конденсатор, заполненный плазмой, ведет себя как источник постоянного напряжения за время длительности импульса ЛИ. Горячие электроны через время τ_ГЭ = d / V (d – расстояние между пластинами конденсатора; V – скорость горячих электронов) достигают отрицательной пластины и замыкают КК-цепь. С момента замыкания цепи начинается разряд конденсатора через катушку с постоянной времени τ_Ц = L / R, где L – индуктивность; R – сопротивление катушки с формированием импульса тока и генерацией в катушке магнитного поля.

Начальные условия переходного процесса коммутации в КК-цепи до прихода ЛИ: u_c(t–) = 0 В; i(t–) = 0 А. В момент (t₀) падения ЛИ на мишень u_c(t₀) = E_с(t₀); i = 0 А (u_c – напряжение на конденсаторе; E_c – ЭДС, определяемая сторонними силами (неэлектрической природы) в плазме; i – ток в КК-цепи). Можно считать, что E_c остается постоянным в течение всей короткой длительности ЛИ τ_и.

После коммутации (время t+) для выбранных на рис. 1 направлений тока и напряжения можно составить дифференциальное уравнение состояния КК-цепи по второму закону Кирхгофа, законам Ома и электромагнитной индукции:

                                –u_c + u_r + u_L = –u_c+ ri + L= 0.                                     (7)

С учетом того, что направление разрядного тока i во внешней цепи и направления электрического поля и напряжения внутри конденсатора противоположны, имеем

                                             i = –С.                                                   (8)

Уравнение (7) после подстановки в него тока (8) преобразуется в однородное дифференциальное уравнение второго порядка:

LСd²u_c / dt² + rСdu_c / dt + u_c = 0.

Соответствующее характеристическое уравнение:

                                         LСp² + rСp + 1 = 0.                                              (9)

Общее решение данного однородного дифференциального уравнения второго порядка:

u_c = A₁e^p1t + A₂e^p2t,

где

                               p₁, p₂ = – ± [r² / 4L² – 1 / LC]^1/2   –                                 (10)

корни характеристического уравнения (9).

Разрядка конденсатора происходит апериодически, поскольку в процессе всего переходного периода напряжение и ток остаются положительными, действительные корни характеристического уравнения (9) имеют отрицательные значения p₂ < p₁ < 0.

Значения A₁ и A₂ находятся по законам коммутации с учетом того, что из-за малости длительности ЛИ ЭДС Е_с не успевает измениться:

u_с(t₀) = E_c(t₀) = u_с(t₀+) = A₁ + A₂;

i(t₀) = –Сdu_c / dt(t₀) = 0 = –Сdu_c / dt(t₀+) = –C(p₁A₁ + p₂A₂).

Отсюда

A₁ = (p₂E_c / (p₂ – p₁)), A₂ = p₁E_c / (p₁ – p₂);

u_c = p₂E_c / (p₂ – p₁)e^p1t + p₁E_c / (p₁ – p₂)e^p2t;

                          i= –Сdu_c / dt = p₁p₂E_cC(e^p1t – e^p2t) / (p₂ – p₁).                               (11)

Подстановка корней из (10) в (11) для тока i апериодического процесса, соответствующего условию r² / 4L² ˃˃ 1 / LC, формулирует выражение

                                          i = (1 – e^–t/τ),                                              (12)

где τ = L / r – постоянная времени цепи, в секундах или Гн/Ом.

Согласно анализу формул (11) и (12) для генерации интенсивного тока и магнитного поля КК-методом требуются не только интенсивные ЛИ (большие значения ЭДС E_с), но и высокие скорости изменения тока. Последнее приводит к необходимости обеспечения по возможности малых значений: радиуса катушки a, сопротивления r и постоянных времени цепи τ_c = rC и τ_L =L / r. Например, магнитное поле в центре катушки B₀ может быть определено протекающим током по формуле магнитного диполя: B₀ = μ₀i / 2a, где a – радиус катушки; μ₀ – вакуумная магнитная проницаемость. Для a = 0,5 мм и тока i = 100 кA получаем B₀ = 125 Tл.

Комплекс «Лазер – система доставки излучения – КК-преобразователь оптического излучения в ток и магнитное поле ДЭК»

1. Лазер с системой доставки излучения. Исследования проведены на лазерной установке с длиной волны излучения λ = 1,06 мкм, энергия в импульсе составляла 25–60 мДж, длительность импульса ~ 10 нс, частота повторения импульсов – 10 Гц. Оптическая схема экспериментальной установки представлена на рис. 3.

Управление лазерной системой производилось с персонального компьютера с помощью интерфейса RS-232. Лазерная система имела следующие технические характеристики:

– энергия в импульсе (максимальная) – 200 мДж;

– длительность импульса – 10 нс;

– частота повторения импульсов: 1–20 Гц;

– расходимость (по уровню 0,86) – 1,0 мрад;

– диаметр пучка – 4,0 мм;

– джиттер – 1,0 нс;

– нестабильность энергии от импульса к импульсу: ±2,5 %.

Энергия лазерных импульсов измерялась с помощью пироэлектрического приемника РЕ50-SH-V2 фирмы Ophir (Israel) в комплекте с индикатором Pulsar-2 и с выводом значений измеренной энергии на экран монитора компьютера. Для регистрации длительности импульсов использовался сверхбыстрый фотодиод серии UPD (UPD-70-UVIR-D) компании Alphalas, Gmbh (Germany), с временем нарастания фронта импульса ≤ 70 пс и осциллограф Tektronix DPO3054 с полосой пропускания 500 МГц.

Диаметр пятна сфокусированного ЛИ на металлической мишени измерялся визуально на длине волны λ = 532 нм путем наблюдения в фокальной плоскости фокусирующего объектива 21 с помощью микроскопа с окуляр-микрометром МОВ-1-15х с общим увеличением Г = 120^х. В режиме регистрации диаметра пятна ЛИ в плоскости фокусировки металлическая мишень удалялась из схемы лазерной установки, в схему вводились удвоитель частоты на кристалле КТР 13 и светофильтры 20, обеспечивающие безопасное наблюдение ЛИ с микроскопом 23.

Исследование влияния углового расхождения ЛИ на характеристики ППП проводились с двумя объективами, обеспечивающими различную расходимость и плотность мощности ЛИ. При использовании объектива с фокусным расстоянием f = 40 мм и диаметром пятна фокусировки на мишени 40 мкм в отсутствие мишени уже при энергии лазерного импульса Е = 20 мДж в воздухе возбуждался устойчивый плазменный факел, возникала интенсивная ударная волна, распространяющаяся навстречу ЛИ. Эксперименты проводились при интенсивности ЛИ на мишени 1,7 · 10¹¹ Вт/см² и длительности импульса τ_и = 10 нс.

Рис. 3. Оптическая схема лазерной установки: 1 – «глухое» зеркало резонатора; 2 – юстируемая телескопическая
система; 3 – электрооптический модулятор на кристалле DKDP; 4 – интерференционный поляризатор; 5 – активный элемент задающего генератора (ø 6,3 × 80 мм); 6 – диафрагма (ø 4,0 мм); 7 – блок поворотных зеркал; 8 – выходное зеркало резонатора; 9 – телескоп; 10 – полуволновая пластина; 11 – активный элемент усилителя (ø 8,0 × 100 мм);
12 – импульсная ксеноновая лампа; 13 – удвоитель частоты на кристалле КТР; 14, 16 – плоскопараллельные пластины, отводящие часть излучения на измеритель энергии лазерного излучения (15) PE50-SH-V2 фирмы Ophir (Israel)
и сверхбыстрый фотодиод (17) UPD-70-UVIR-D компании Alphalas, Gmbh (Germany), для измерения длительности лазерного импульса; 18 – осциллограф Tektronix DPO3054; 19 – телескоп (Г = 3^х); 20 – сменные светофильтры;
21 – объектив (f = 40 мм), фокусирующий лазерное излучение на металлическую мишень 22;
23 – микроскоп с окуляр-микрометром МОВ-1-15х

Fig. 3. Laser optical graph: 1 – nontransmitting mirror of a resonator; 2 – adjustable telescopic system;
3 – electro-optical modulator on a DKDP crystal; 4 – interference polarizer; 5 – active element of the master oscillator with dimensions ø 6.3 × 80 mm; 6 – diaphragm ø 4.0 mm; 7 – block of rotary mirrors; 8 – resonator output mirror; 9 – telescope; 10 – half-wave plate; 11 – active element of the amplifier with dimensions ø 8.0 × 100 mm; 12 – pulsed xenon lamp;
13 – frequency doubler on a KTP crystal; 14, 16 – plane-parallel plates diverting part of the radiation to the laser radiation energy meter (15) PE50-SH-V2 by Ophir (Israel) and ultrafast photodiode (17) UPD-70-UVIR-D by Alphalas, Gmbh
(Germany) for measuring laser pulse duration; 18 – Tektronix DPO3054 oscilloscope; 19 – telescope with G = 3^x;
20 – replaceable light filters; 21 – objective lens f = 40 mm focusing laser radiation on a metal target 22;
23 – microscope with ocular-micrometer MOV-1-15x

В результате экспериментов было установлено, что возбуждаемая плазма сильно поглощает и рассеивает ЛИ и пропускание излучения плазмой с увеличением энергии светового импульса практически не увеличивается (таблица).

Результаты экспериментов

Experimental results

Согласно данным таблицы ослабление ЛИ, прошедшего плазму, образованную в воздухе, резко возрастает при превышении интенсивности излучения значений ~ 10¹¹ Вт/см². Увеличение ослабления сопровождалось переходом от плазменного факела к сферическому континууму молочного цвета. Можно полагать, что это преобразование плазмы в воздухе вызвано резким возрастанием многократного рассеяния ЛИ при превышении его интенсивности уровня ~ 10¹¹ Вт/см².

2. Рассеяние плазмой лазерного излучения. Проходящее к мишени через плазму ЛИ ослабляется в результате рассеяния на микрочастицах плазмы. Анализ средней разности фаз δ волн, пришедших от двух рассеивающих центров внутри рассевающего объема радиуса R, в зависимости от угла рассеяния γ, позволяет определить критический угол γ_кр = λ / R, при котором δ = 2π. Рассеяние излучения под углами γ ˂˂ γ_кр является когерентным, его интенсивность ~ N²; под углами γ >> γ_кр – некогерентным, интенсивность ~N, где N – число рассеивающих частиц в освещенном объеме. Решение уравнения переноса в приближении малых углов позволяет выделить две области в пучке излучения, прошедшего рассеивающую среду: ближняя, характеризуемая наличием как нерассеянного, так и однократно рассеянного излучения с интенсивностью, убывающей по закону Бугера, и дальняя, отличающаяся преобладанием многократно рассеянного излучения. Соответственно, пространственная фигура, образуемая уровнями постоянной мощности излучения, может иметь максимум на оси пучка [3].

Согласно теоретическому анализу в малоугловом приближении для уменьшения доли многократного рассеяния по сравнению с однократным следует уменьшать угловое расхождение падающего излучения [3]. При использовании линзы с фокусным расстоянием f = 180 мм диаметр пятна фокусировки составлял 300 мкм, и при увеличении энергии ЛИ до 100 мДж (интенсивность излучения достигала значения E_L = 1,4 · 10¹⁰ Вт/см²) плазма в воздухе не возбуждалась и вся энергия ЛИ доставлялась до мишени.

Помимо сильного ослабления, в плазме наблюдается также значительная нестабильность прошедшей через плазменный факел энергии ЛИ, что может быть связано с неустойчивостью плазмы в начальный период ее образования.

В экспериментах с мишенью при высоких плотностях мощности ЛИ часть его энергии поглощается и рассеивается ППП, эффективность взаимодействия с пластиной-мишенью, генерирующей горячие электроны, зависит от параметров системы доставки излучения к мишени. Эффективность растет с уменьшением угловой расходимости ЛИ и увеличением интенсивности нерассеянной составляющей излучения в соответствии
с представленным теоретическим анализом.

Исследования доказали, что энергоэффективные оптико-электрические преобразователи для ДЭК могут быть созданы на основе КК-метода, в частности путем замены пластин конденсатора (см. рис. 1) концентрическими медными кольцами с расстоянием между ними d и щелью в кольце вместо отверстия. Вращение (перемещение) кольца-мишени относительно оси ЛИ исключает возможность прожига мишени.

Конденсатор-катушка как преобразователь оптического излучения для динамических электротехнических комплексов

Энергоэффективные преобразователи оптического излучения для ДЭК могут быть созданы на основе КК-метода путем, например, замены пластин конденсатора (см. рис. 1) вращающимися концентрическими медными кольцами с расстоянием между ними d и щелью во внешнем кольце вместо отверстия. Вращение (перемещение) мишени относительно оси ЛИ, как было отмечено выше, исключает возможность прожига мишени.

Практический интерес представляет оценка параметров частотного неодимового лазера, необходимых для получения в катушке тока порядка 1 кА при радиусе витков до 10 мм и электрическом сопротивлении 1 Ом. Для данных параметров и схемы (рис. 1), проводя соответствующие расчеты, устанавливаем, что для получения тока в 1 кА будет достаточно лазерной интенсивности 6 · 10¹¹ Вт/см² при длительности лазерного импульса 10 нс и радиусе фокальной перетяжки 20 мкм. Энергия лазерного импульса при этом будет около 60 мДж. В экспериментальной схеме катушка может содержать 1 виток медной проволоки радиусом витка 10 мм и диаметром провода 0,2 мм (сопротивление – 0,034 Ом). Конденсатор можно использовать с площадью медных пластин 0,1 см² (например, квадрат 3 × 3 мм) и расстоянием между пластинами в 1 мм. Тогда ток составит 1,01 кА, напряжение на конденсаторе – 6,5 кВ, магнитное поле – 0,06 Тл. Если увеличить сопротивление до 1 Ом (например, взять нихромовый виток вместо медного), ток при тех же остальных параметрах упадет до 0,5 кА, и потребуется увеличить интенсивность до 3 · 10¹² Вт/см², например уменьшив радиус фокальной перетяжки до 10 мкм, чтобы вернуться к току в 1 кА.

Обсуждение

Согласно формулам (11), (12) для генерации интенсивного магнитного поля КК-методом требуются не только высокие мощности ЛИ (большие значения ЭДС E_c), но и высокие скорости изменения тока, соответственно, малые значения постоянных времени цепи τ_c = rC и τ_L = L / r.

Численным моделированием оценены параметры КК-преобразования в двух режимах: когда плотность плазмы стремится к нулю, т. е. при низких интенсивностях ЛИ I < 2–3 · 10¹¹ Вт/см², и когда конденсатор заполнен плазмой, 10¹⁶ Вт/см².

Переход с первого режима на второй начинается с интенсивностей ЛИ ˃ 5 · 10¹² Вт/см² при тех же остальных параметрах КК-схемы.

Расчетные характеристики КК-оптоэлектри-ческого преобразователя с неодимовым частотным лазером:

– интенсивность ЛИ – 6 · 10¹¹ Вт/см²;

– длительность лазерного импульса – 10 нс;

– энергия в лазерном импульсе – 60 мДж;

– частота – 10 Гц;

– радиус фокальной перетяжки – 20 мкм;

– радиус витка катушки a (см. рис. 1) – 10 мм;

– расстояние между пластинами конденсатора d (см. рис. 1) – 1 мм;

– ток I – 1,01 A;

– напряжение U_C  на конденсаторе – 6,5 кВ;

– плотность магнитного потока – 0,06 Тл.

Выводы

1. Проведены модельные расчеты схемы «конденсатор-катушка» электрической цепи.

2. Экспериментально обнаружена зависимость ослабления излучения неодимового лазера плазмой в зависимости от интенсивности и углового расхождения излучения. Можно полагать, что это ослабление вызвано резким возрастанием многократного рассеяния ЛИ в воздухе при превышении его интенсивности уровня ~ 10¹¹ Вт/см².

3. Предложена КК-модель преобразователя ЛИ для бесколлекторного электродвигателя, в которой конденсатор с двумя плоскими пластинами заменен двумя концентрическими электродами с тем же промежутком. Для прохождения ЛИ к внутреннему кольцу по окружности внешнего кольца изготовлена прорезь шириной a, где a – радиус отверстия в пластине конденсатора исходной КК-модели.

Кольцевая прорезь позволяет смещать фокальное пятно на поверхности внутреннего кольца-мишени относительно неподвижной оптической оси ЛИ, что способствует повышению мощности и ресурса электродвигателя.

Импульсный режим обеспечивает необходимые временную и логическую программы работы электродвигателя в системах управления.

1. Terent'ev V. E. Optoelektronnye preobrazovateli energii v robototekhnicheskikh kompleksakh upravleniia i kontrolia dvizheniia sudna. Morskaia robototekhnika [Optoelectronic energy converters in robotic systems for controlling and controlling the movement of a vessel. Marine Robotics]. Materialy Mezhdunarodnoi konferentsii po morskoi robototekhnike v osvoenii okeana (Sankt-Peterburg, 17-19 sentiabria 2019 g.). Pp. 417-423.

2. Terent'ev V. E., Ochina L. B. Robotizirovannyi kompleks upravleniia i kontrolia dvizheniia samokhodnogo elektroprivodnogo promernogo sudna [Robotic complex for control and monitoring of movement of self-propelled electrically driven measuring vessel]. Vestnik Gosudarstvennogo universiteta morskogo i rechnogo flota imeni admirala S. O. Makarova, 2020, vol. 12, no. 1, pp. 165-173.

3. Terent'ev V. E. Modelirovanie elektricheskikh tsepei i sistem s optiko-elektronnymi ustroistvami: monografiia [Modeling electrical circuits and systems with optoelectronic devices: monograph]. Saint-Petersburg, Izd-vo SPGUVK, 2009. 201 p.

4. Terentiev V. E., Artamokhin S. G., Pikhtin N. A., Shvarts M. Z. Modeling the complex delivery of electric energy by opticalchannel to dynamic electromechanical transformer. International Journal of Mechanical and Technology, 2018, no. 9 (2), pp. 765-774.

5. Terent'ev V. E. Beskollektornaia elektricheskaia mashina [Brushless electric machine]. Patent RF no. 2563974; 27.09.2015.

6. Korobkin V. V., Motylev S. L. On a possibility of using laser radiation for generation of strong magnetic fields. Soviet Technical Physics Letters, 1979, no. 5, p. 474.

7. Seely J. F. Pulsed megagaus fields produced by laser-driven coils. Journal of Applied Physics, 1983, no. 31, pp. 37-43.

8. Daido H., Miki F., Mima K., Fujita M., Sawai K., Fujita H., Kitagawa Y., Nakai S., Yamanaka C. Generaition of a Strong Magnetic Field by an Intense CO2 Laser Pulse. Physical Review Letters, 1986, no. 56, pp. 846-849.

9. Tikhonchuk V. T., Bailly-Grandvaux M., Santos J. J. Quasistationary magnetic field generation with a laser-driven capacitor-coil assembly. Physical Review, 2017, no. 96, p. 023202.

10. Spence D. E., Kean P. N., Sibbett W. 60-fsec pulse generation from a self-modelocked Ti: sapphire laser. Optics Letters, 1991, vol. 16, no. 1, pp. 42-44.

11. Albert O., Wang H., Liu D., Chang Z., Mourou G. Generation of relativistic intensity pulses at a kilohertz repetition rate. Optics Letters, 2000, vol. 25, pp. 1125-1127.

12. Keller U. Recent developments in compact ultrafast lasers. Nature, 2003, vol. 424, no. 6950, pp. 831-838.

13. Terent'ev V. E. Beskollektornyi elektrodvigatel' [Brushless electric motor]. Patent RF no. 2727934; 27.07.2020.

14. Liu X. L., Lu X., Ma J. L., Du Z. G., He Y. Pre-pulse characterization of femtosecond laser pulse by filamentation in transparent media. Review of Scientific Instruments, 2014, vol. 85, p. 126103.