Russian Federation
Grozny State Petroleum Technological University (Candidate of Technical Sciences, Assistant Professor; Assistant Professor of the Department of Automation of Technological Processes and Production)
Russian Federation
Grozny, Grozny, Russian Federation
Russian Federation
The improvement of electrophysical and electrochemical processing technologies is a key task for modern mechanical engineering, especially in the production of high-precision parts of complex shapes, such as turbine blades and molds. One of the promising directions is the use of processing methods with profile electrodes with vertical feed, which provides increased accuracy, process stability and reduced tool wear. However, the issues of dynamic modeling of such a drive, which are critically important for predicting the behavior of the system and optimizing its operation, have not been sufficiently studied. The purpose of this work is to develop a dynamic model of the vertical feed drive of the profiling electrode and analyze its transients to optimize technological parameters. The study presents a detailed kinematic drive scheme. The methodology is based on a strict energy approach to reducing the parameters of the kinematic target to the motor shaft. Based on the obtained equations of motion, a computer model has been developed in the Simulink environment. The results of modeling transients during direct start-up confirmed the stability of the system and the correctness of the selected parameters. The analysis revealed the oscillatory nature of the transient process caused by elastic bonds, and showed a smooth transition to a steady state with a slight overshoot, which is acceptable for high-precision positioning tasks. An effective linear model of an electromechanical actuator is presented, which has proven its adequacy as a basic tool. The analysis showed that in order to further improve the accuracy of the predictive ability of the model, it is necessary to take into account significant nonlinear factors: variable stiffness, kinematic gaps, temperature deformations and gradual wear of nodes.
vertical feed, electrosparking, profiling electrode, electric drive, mathematical modeling, system dynamics, transients, Simulink
Введение
Совершенствование технологий электрофизической и электрохимической обработки материалов остается важной задачей в современном машиностроении и приборостроении. Одним из перспективных направлений является разработка и оптимизация методов обработки с использованием профилирующих электродов, которые позволяют повысить точность, производительность и качество поверхностного слоя деталей сложной формы. Особый интерес представляет вертикальная подача профилирующего электрода, поскольку она обеспечивает:
– повышение точности обработки за счет минимизации боковых отклонений инструмента;
– улучшение стабильности процесса благодаря равномерному распределению нагрузки на электрод;
– снижение износа инструмента за счет оптимизации траектории движения;
– возможность обработки сложнопрофильных поверхностей (например, лопаток турбин, пресс-форм, микроструктурированных поверхностей).
Несмотря на существующие разработки в области электроэрозионной и электрохимической обработки, вопросы моделирования вертикальной подачи профилирующего электрода изучены недостаточно [1, 2]. В частности, требуют уточнения вопросы:
– влияния кинематики подачи на точность формообразования;
– тепловых и электродинамических эффектов при вертикальном перемещении электрода;
– оптимальных режимов обработки для различных материалов.
Разработка математической и компьютерной модели вертикальной подачи профилирующего электрода позволит:
– прогнозировать качество обработки;
– оптимизировать технологические параметры;
– снизить энергозатраты и себестоимость производства.
Целью работы являются разработка динамической модели привода вертикальной подачи профилирующего электрода и анализ ее переходных процессов.
Модель вертикальной подачи профилирующего электрода
При моделировании электроприводов механическую часть часто представляют упрощенными схемами, где жесткие связи считаются абсолютно твердыми, а второстепенные массы учитываются приближенно. Для этого все параметры кинематической цепи приводят к одной расчетной скорости – скорости вала двигателя.
Чтобы упрощенная схема корректно отражала реальную систему, необходимо соблюдать закон сохранения энергии. Это означает, что в процессе приведения должны сохраняться:
– суммарная кинетическая и потенциальная энергия системы;
– работа всех сил и моментов на возможных перемещениях.
Таким образом, при приведении момента инерции вращающихся элементов (со скоростью ωᵢ) или масс, движущихся поступательно (со скоростью V), к расчетной скорости ω1 важно учитывать эти энергетические условия:
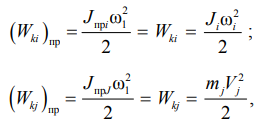
где Wki – кинетическая энергия i-го вращающего момента; Jпрi – приведенный к валу двигателя момент инерции i-го элемента; Ji – собственный момент инерции i-го элемента; Wkj – кинетическая энергия i-го поступательно движущегося элемента; JпрJ – приведенный к валу двигателя момент инерции j-го элемента; mj – масса i-го элемента.
При преобразовании вращательных φᵢ и поступательных S перемещений важно учитывать, что передаточное отношение и радиус приведения зави сят от соотношения скоростей элементов системы. Следовательно, связь между перемещениями в общем виде выражается следующим образом [3, 4]:
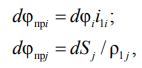
где i1i – передаточное отношение от вала двигателя к i-му вращающемуся звену; ρ1j – радиус приведения от вала двигателя к j-му поступательно движущемуся звену.
Если кинематические связи являются линейными (i1ᵢ = const, ρ1j = const), то приведенные перемещения определяются по формулам:
– для вращательного движения:
![]()
– для поступательного движения:
![]()
При приведении жесткостей механических связей необходимо соблюдать условие сохранения потенциальной энергии деформации упругих элементов [5–7]:
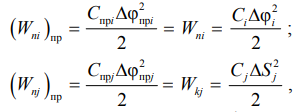
где Wni – потенциальная энергия деформации i-го упругого элемента при кручении; Wnj (kj) – потенциальная энергия деформации j-го упругого элемента при растяжении/сжатии; C – жесткость. Отсюда получим формулы приведения:
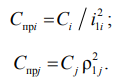
Приведение моментов и сил нагрузки в кинематической цепи выполняется исходя из условия равенства элементарной работы на возможных перемещениях [8, 9]:
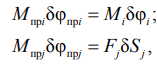
где Mпрi – приведенный к валу двигателя момент от i-го звена; Mпрj – приведенный к валу двигателя момент от j-й силы; δ – элементарная работа; Fj – сила, действующая на j-й элемент.
Таким образом, приведенные значения определяются соотношением
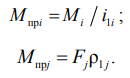
Кинематическая схема привода вертикальной подачи профилирующего электрода включает следующие компоненты (рис. 1).
1. Электропривод – основной источник механического движения.
2. Конические шестерни передают вращение без изменения передаточного отношения (i = 1).
3. Винтовой механизм преобразует вращательное движение в поступательное перемещение.
4. Рабочий стол с профильным электродом подвижная платформа для выполнения обработки.
5. Линейные направляющие обеспечивают точное позиционирование стола.
6. Компенсационные пружины (устранение перекосов и вибраций).
7. Амортизаторы (снижение колебаний и повышение устойчивости системы).
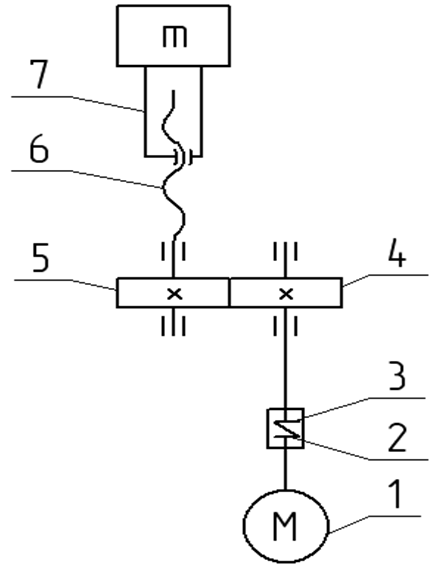
Рис. 1. Кинематическая схема привода вертикальной подачи профилирующего электрода:
M – момент двигателя; m – масса стола с электродом; 1–7 – номера звеньев
Fig. 1. Kinematic diagram of the profile
electrode vertical feed:
M – motor torque; m – mass of the table with electrode; 1–7 – link numbers
Параметры кинематической схемы:
– передаточное отношение зубчатой пары: i = 1 (прямая передача без изменения скорости);
– радиус приведения винтовой передачи (винт-гайка): ρ = 0,005 м;
– масса подвижного стола с ванной и профилирующим электродом: m = 20 кг.
Жесткости механических связей и моменты инерции элементов привода приведены в табл. 1: звенья 1–7 соответствуют элементам кинематической цепи на рис. 1, для каждого звена указаны: J – момент инерции, c – жесткость.
Таблица 1
Table 1
Параметры моментов инерции и жесткостей элементов привода
Parameters of moments of inertia and stiffnesses of the drive elements
|
Параметр |
Звено |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
J, кг·м2 |
0,0025 |
0,0027 |
0,002 |
– |
|||
|
c, Н·м |
– |
2,77 · 106 |
1 · 108 |
1 · 108 |
|||
В табл. 2 представлены расчетные значения моментов инерции и жесткостей передач, приведенных к валу двигателя.
Таблица 2
Table 2
Приведенные к валу двигателя моменты инерции и жесткости
Moments of inertia and stiffnesses reduced to the motor shaft
|
Параметр |
Звено |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
J, кг·м2 |
0,0025 |
0,0027 |
0,002 |
0,00005 |
|||
|
c, Н·м |
– |
2,77 · 106 |
1 · 108 |
2 500 |
|||
На основании данных, представленных в табл. 2, производим:
1. Выделение доминирующих масс и основных упругих элементов системы.
2. Сравнительный анализ их влияния на динамику привода.
3. Построение упрощенной расчетной модели механической части привода вертикальной подачи профилирующего электрода.
Для кинематической схемы привода (см. рис. 1) уравнения движения вертикальной подачи электрода записываются следующим образом:
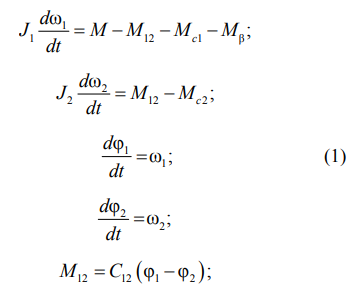
![]()
где β – угол поворота вала двигателя; M12 – упругий момент в связи 1-й и 2-й массами; Mβ – момент двигателя; Mc1 – момент сопротивления, приведенный к валу двигателя; Mc2 – момент сопротивления на винтовой паре; С12 – жесткость упругой связи между 1-й и 2-й массами.
Будем полагать, что момент двигателя линейно зависит от скорости:
![]()
Для численного решения системы уравнений (1) была разработана компьютерная модель в среде Simulink [10]. На рис. 2 представлена блок-схема модели привода вертикальной подачи профилирующего электрода, включающая следующие основные компоненты:
– блоки, соответствующие уравнениям движения системы;
– элементы, моделирующие электромеханические преобразования;
– компоненты, отражающие динамику механической части привода.
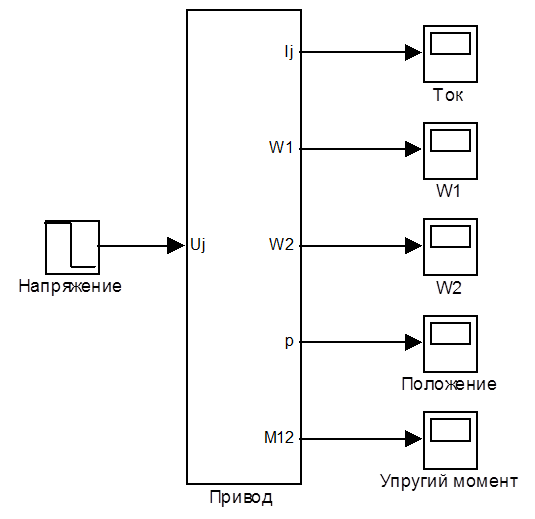
Рис. 2. Simulink-модель привода вертикальной подачи электрода
Fig. 2. Simulink-the model of the vertical electrode feed
Блок «Привод» (см. рис. 2), в свою очередь, состоит из блока, моделирующего электрическую часть электродвигателя, и блока, моделирующего механику электропривода в целом. Модель может быть расширена за счет блоков, учитывающих нелинейные характеристики упругих связей и демпфирования.
Переходный процесс прямого пуска электропривода вертикальной подачи электрода представлен на рис. 3.
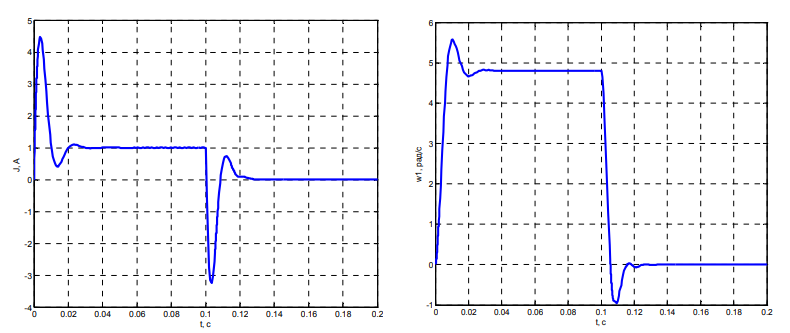
а б
Рис. 3. Переходный процесс прямого пуска электропривода вертикальной подачи электрода:
а – изменения тока якоря двигателя; б – скорость вращения 1-й массы
Fig. 3. The transient process of the direct start-up of the electric drive of the vertical electrode feed:
а – current; б – speed of rotation of the 1st mass
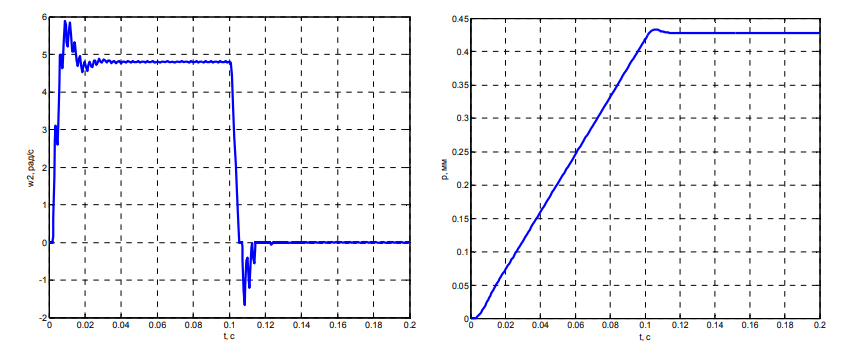
в г
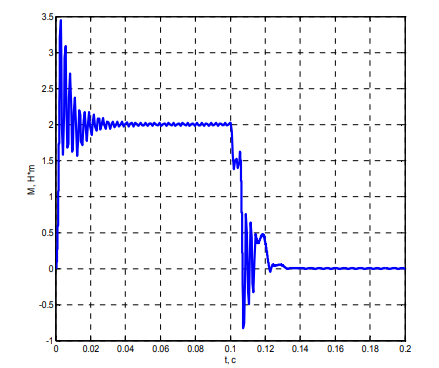
д
Рис. 3 (окончание). Переходный процесс прямого пуска электропривода вертикальной подачи электрода:
в – скорость вращения 2-й массы; г – положение привода; д – упругий момент
Fig. 3 (ending). The transient process of the direct start-up of the electric drive of the vertical electrode feed:
в – speed of rotation of the 2nd mass; г – drive position; д – elastic moment
В ходе исследования переходных процессов привода вертикальной подачи профилирующего электрода были получены графики, наглядно демонстрирующие динамику системы при прямом пуске. Анализ этих графиков позволяет сделать следующие выводы о работе системы.
График изменения тока якоря двигателя (см. рис. 3, а) показывает характерный для электроприводов переходный процесс с резким броском тока в начальный момент пуска, что объясняется необходимостью преодоления статического момента сопротивления. Максимальное значение тока достигается в момент трогания, после чего наблюдается его постепенное снижение по мере нарастания скорости вращения и увеличения противо-ЭДС. Такой характер кривой полностью соответствует теоретическим представлениям о работе двигателя постоянного тока и подтверждает корректность моделирования электрической части системы.
Скоростные характеристики первой и второй масс (см. рис. 3, б, в) демонстрируют колебательный характер переходного процесса, что обусловлено наличием упругих связей в механической части привода. Первая масса (график скорости ω1) показывает плавный выход на установившуюся скорость с небольшим перерегулированием, типичный для систем с упругими элементами. Вторая масса (график скорости ω2) отражает более сложную динамику с выраженными затухающими колебаниями, что объясняется влиянием механического резонанса в системе. Различие в поведении масс указывает на присутствие упругих деформаций в кинематической цепи.
График углового положения φ (см. рис. 3, г) демонстрирует высокую устойчивость системы: после завершения переходных процессов значение стабилизируется на заданном уровне без остаточных колебаний. Это говорит о верно подобранных параметрах системы и отсутствии статических погрешностей позиционирования.
Анализ осциллограммы упругого момента M12 (см. рис. 3, д) позволил выявить динамику силового взаимодействия элементов привода, опосредованного упругими связями. Наблюдаемые колебания момента служат верификацией наличия существенных упругих деформаций, что обусловливает необходимость их учета на этапе проектирования. Ключевыми критериями для оценки виброустойчивости системы выступают амплитуда и декремент затухания данных колебаний. Изучение переходных характеристик позволяет сделать вывод о том, что созданная модель является работоспособной, а параметры привода были выбраны верно. Наблюдаемые процессы соответствуют теоретическим ожиданиям для подобных систем. Незначительное перерегулирование и быстрое затухание колебаний указывают на отличные динамические характеристики системы, что является критически важным для точного позиционирования профилирующего электрода в ходе обработки.
Учет нелинейных эффектов в динамике привода
Разработанная математическая модель привода вертикальной подачи профилирующего электрода, представленная в работе, основана на линейных приближениях, что позволяет эффективно анализировать основные динамические характеристики системы. Однако для повышения точности моделирования и соответствия реальным условиям эксплуатации необходимо учитывать нелинейные эффекты, возникающие в процессе электроэрозионной обработки. Эти эффекты могут существенно влиять на точность позиционирования, стабильность процесса и долговечность оборудования.
В реальной кинематической цепи привода (см. рис. 1) жесткость передач не является постоянной величиной. Это обусловлено:
– нагрузочной деформацией элементов (зубчатых колес, валов, винтовых пар), которая приводит к изменению жесткости в зависимости от приложенного момента;
– наличием зазоров в передачах, что вызывает нелинейную характеристику при реверсе движения;
– температурными деформациями, которые изменяют геометрию и упругие свойства элементов системы.
Демпфирующие свойства системы также имеют нелинейный характер:
– сухое трение (трение покоя) проявляется в момент трогания и изменяет начальные условия переходного процесса;
– вязкое трение может зависеть от скорости нелинейно, особенно при высоких скоростях вращения.
В процессе электроэрозионной обработки выделяется значительное количество тепла, что приводит к тепловым деформациям элементов привода, влияющим на точность позиционирования, а также к изменению механических свойств материалов (снижению жесткости, увеличению зазоров).
Следует отметить, что профилирующий электрод подвергается износу в процессе обработки, что приводит к изменению геометрии электрода, влияющему на точность формообразования и увеличению зазора между электродом и заготовкой, что требует адаптации режимов обработки.
Заключение
Разработана математическая модель вертикальной подачи профилирующего электрода, интегрирующая ключевые динамические параметры электропривода: моменты инерции, жесткость кинематических связей и демпфирующие свойства системы. На основе полученных уравнений сформирована расчетная схема, позволяющая проводить анализ переходных процессов при прямом пуске привода.
Проведенное имитационное моделирование в среде Simulink верифицировало устойчивость системы и установило влияние параметров привода на его динамические характеристики. В ходе работы определено, что плавный выход на установившийся режим обеспечивается линейной зависимостью момента двигателя от скорости. Анализ переходных процессов, таких как ток статора, положение вала, скорость вращения и упругий момент, показал стабильность системы, которая соответствует требованиям точной работы при электроэрозионной и электрохимической обработке. Выявленные результаты могут быть использованы при оптимизации режимных и конструктивных параметров привода и в дальнейшем использованы для повышения точности обработки сложнопрофильных деталей, например турбинных лопаток и пресс-форм. Дальнейшим направлением исследований может являться внедрение в модель различных нелинейных эффектов, включая температурные деформации и износ инструмента, актуальных при обработке сложных поверхностей
с повышенной точностью. Данный подход перспективен при создании особо точных систем управления, применяемых в реальных производственных условиях.
1. Ioffe V. F., Korenblyum M. V., Shavyryn V. A. Avtomatizirovannye elektroerozionnye stanki [Automated Electrical Discharge Machines]. Leningrad, Mashinostroenie Publ., 1984. 227 p.
2. Eliseev Yu. S., Saushkin B. P. Elektroerozionnaya obrabotka izdeliy aviatsionno-kosmicheskoy tekhniki [Electrical discharge machining of aerospace products]. Moscow, Izd-vo MGTU im. N. E. Baumana, 2010. 437 p.
3. Avdeeva O. V., Semenov A. D., Nikitkin A. S. Modelirovanie sistemy avtomaticheskogo regulirovaniya mezhlektrodnogo zazora pri elektroerozionnom profilirovanii almaznykh krugov. Problemy avtomatizatsii i upravleniya v tekhnicheskikh sistemakh [Modeling of the automatic regulation system of the interelectrode gap during electrical discharge profiling of diamond wheels. Problems of automation and control in technical systems]. Penza, Izd-vo PGU, 2009. Pp. 290-294.
4. Tarasik V. P. Matematicheskoe modelirovanie tekhnicheskikh system [Mathematical modeling of technical systems]. Moscow, Infra-M Publ., 2017. 160 p.
5. Avdeeva O. V., Semenov A. D., Artamonov D. V. Modelirovanie sistem upravleniya. Laboratornyy praktikum [Modeling of control systems. Laboratory practical training]. Penza, Izd-vo PGU, 2019. 80 p.
6. Feofanov A. N. Razrabotka, modelirovanie i optimi-zatsiya raboty mekhatronnykh system [Development, modeling and optimization of mechatronic systems]. Moscow, Akademiya Publ., 2018. 320 p.
7. Popov E. P. Nelineynye sistemy avtomaticheskogo regulirovaniya [Nonlinear automatic control systems]. Moscow, Nauka Publ., 1988. 255 p.
8. Nikitkin A. S., Semenov A. D. Modelirovanie sistemy avtomaticheskogo regulirovaniya mezhèlektrodnogo zazora pri èlektroèrozionnom profilirovanii almaznykh krugov [Modeling of the interelectrode gap control system for electrical discharge profiling of diamond wheels]. Nadëzhnost' i kachestvo: trudy Mezhdunarodnogo simpoziuma. Penza, Izd-vo PGU, 2009. Pp. 270-273.
9. Krishan R. Electric motor drives: Modeling, analysis and control. Upper Saddle River, New Jersey, Prentice-Hall, 2001. 626 p.
10. Mohan H. Advanced Electric Drives: Analysis, Control, and Modeling Using MATLAB/Simulink. Hoboken, New Jersey, Wiley, 2011. 210 p.















