Russian Federation
In the context of rising energy prices and stricter environmental requirements, enterprises strive to minimize energy consumption without compromising product quality and productivity. Reducing fuel gas consumption in production processes plays a key role in increasing economic efficiency and reducing negative environmental impacts. The most significant consumers of fuel gas are the energy sector, the processing industry and oil refining. For oil refining processes, tubular furnaces are often used, designed to heat raw materials to the required temperature. The introduction of more advanced automated control systems for heating raw materials in a tubular furnace will significantly reduce costs, increase energy efficiency and reduce emissions of pollutants. To increase control efficiency, a multi-stage system for automatic temperature control at the outlet of a tubular furnace is proposed. The consumption of fuel gas supplied to the burners and the temperature of the flue gases at the boundary of the radiant and convective chambers of the furnace are used as auxiliary adjustable parameters. A mathematical model of a multistage automatic control system for a tubular furnace is proposed. The tuning parameters of the regulators of a multistage system are calculated based on the Ziegler-Nichols method, taking into account the mutual influence of the regulator parameters. Transients in control and disturbing effects in single-circuit, traditional two-stage and three-stage systems are considered. A comparative analysis of the characteristics of the transient process of single-circuit, two-stage and three-stage automatic control systems is carried out. It is shown that the use of the proposed multi-stage structure of the control system will optimize the operation and improve the quality of control of tubular furnaces, as well as similar technological facilities with significant transport and capacitive delays with high inertia. The practical implementation of multi-stage systems is carried out on the basis of standard functional blocks of PID control of industrial controllers, which expands the application of the proposed approach.
mathematical model, tubular furnace, multistage control system, single-circuit system, automatic control, transients
Введение
В качестве объекта исследования рассматривается трубчатая печь установки У-121 стабилизации газового конденсата Астраханского газоперерабатывающего завода ООО «Газпром переработка». Печь представляет собой аппарат, состоящий из радиантной и конвективной камер и дымовой трубы высотой 60 м. Подовая часть радиантной камеры печи оборудована газовыми горелками, расположенными симметрично. Аппарат используется для подогрева стабильного конденсата колонны стабилизации. Внутренняя температура радиантной и конвекционной камеры составляет 330 и 270 ºC соответственно.
Из-за инерционности процесса передачи тепла от дымовых газов через стенку змеевика к находящемуся внутри продукту переходный процесс по каналу регулирования «расход топливного газа – температура стабильного конденсата на выходе печи» занимает несколько десятков минут. В таких условиях использование одноконтурной системы автоматического регулирования при наличии внешних возмущений приводит к значительным динамическим отклонениям и длительному времени установления режима.
Анализ релевантных работ
В результате изучения научных источников по вопросам управления трубчатой печью определены возможные решения данной проблемы.
В работе [1] приводится общая постановка проблемы регулирования трубчатой печи. Одной из главных причин сложности в регулировании трубчатой печи является большая инерционность по основным каналам регулирования. В статье приводится несколько решений, за счет которых возможно улучшить качество регулирования переходным процессом: выбор в качестве вспомогательного параметра регулирования температуры газов на границе радиантной и конвективной камер; компенсация возмущающего воздействия в виде изменения расхода продукта через трубчатую печь; компенсация возмущающего воздействия в виде изменения давления топливного газа. Однако в работе математическая модель представлена в упрощенном виде, без учета сложных динамических характеристик реального объекта управления.
В статье [2] представлен обзор существующих средств и систем управления подогревателями нефти и газа, используемыми на скважинных площадках и на установках первичной подготовки продукции на объектах газонефтедобычи. Рассмотрена задача синтеза оптимизированной системы управления для трубчатой блочной печи ПТБ-5-40Э, описываются этапы верификации модели и анализа ка-
чества регулирования с использованием MATLAB/Simulink. В качестве управляющего элемента используется нейроконтроллер, что создает определенные трудности при практическом внедрении полученных результатов.
Изучение работ по проблеме управления трубчатой печью показало, что вопросу значительной инерционности объекта управления уделяется недостаточно внимания, поэтому в данной статье будут рассмотрены варианты модернизации систем регулирования с применением каскадных структур.
В статье [3] представлены результаты разработки одноконтурной и каскадной систем автоматического регулирования с адаптивным нечетким регулятором для регулирования уровня дизельного топлива в барометрическом конденсаторе вакуумного блока установки ЭЛОУ-АВТ-6. В работе были реализованы одноконтурные системы автоматического регулирования с цифровым ПИД-регулятором, стандартным нечетким ПИД-регулятором, нечетким ПИД-регулятором с использованием 2-D интерполяционной таблицы в Simulink. Результаты исследования показывают, что наименьшую динамическую ошибку демонстрирует каскадная САР с ПИ и ПИД-регуляторами, но при этом значительно увеличивается длительность переходных процессов.
В работе [4] демонстрируется возможность создания эффективной каскадной системы автоматического управления с нечеткой динамической коррекцией одного из параметров регулятора основного контура. Представлены переходные процессы, полученные без применения вычислительных процедур, обычно используемых при нечеткой настройке параметров традиционных ПИД-регуляторов. Недостатком предложенного подхода является осуществление динамической коррекции только для одного параметра регулятора в основном контуре каскадной системы.
В статье [5] рассматриваются вопросы синтеза автоматических регуляторов для объектов с распределенными параметрами и значительным емкостным запаздыванием. На основании синтеза параметров распределенных регуляторов предложены методы реализации адаптивной настройки различных регуляторов. Однако практическая реализация результатов вызывает определенные трудности,
т. к. требует значительной вычислительной мощности применяемых промышленных контроллеров.
По результатам обзора установлено, что ни одно из рассмотренных решений не учитывает наличие множественности воздействующих возмущений, сложной динамики объекта, а также возможность практической реализации результатов исследований с использованием типовых технических средств автоматизации.
В этой связи предлагается усложнение структуры каскадной системы путем внедрения дополнительных регулирующих устройств на основе типовых законов регулирования по промежуточным параметрам, имеющим лучшие динамические характеристики по сравнению с основной регулируемой величиной.
Математическая модель объекта управления
Упрощенная технологическая схема рассматриваемой трубчатой печи на установке У-121 приведена на рис. 1.
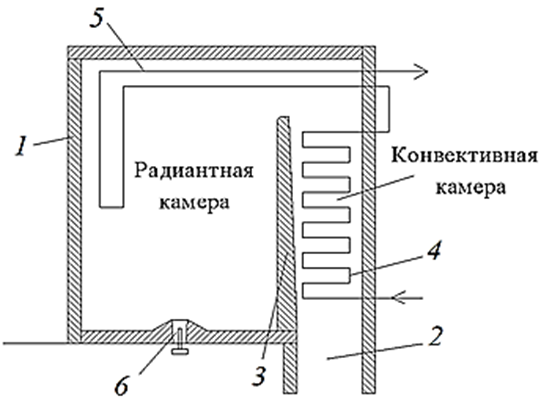
Рис. 1. Схема трубчатой печи:
1 – стенка печи; 2 – дымоход; 3 – перегородка; 4 – трубный змеевик конвективной камеры;
5 – трубный змеевик радиантной камеры; 6 – газовая горелка
Fig. 1. Diagram of a tubular furnace:
1 – furnace wall; 2 – chimney; 3 – partition; 4 – convection chamber coil;
5 – radiant chamber coil; 6 – gas burner
На основе уравнения теплового баланса [1] была получена математическая модель для расчета температуры стабильного конденсата на выходе трубчатой печи в зависимости от расхода топливного газа, подаваемого на горелки печи.
Математическая модель представлена в виде дифференциального уравнения
(1)
где С – теплоемкость стабильного конденсата;
d – внутренний диаметр трубопровода змеевика; дифференциал 
определяет скорость изменения температуры стабильного конденсата по длине змеевика, а 
– количество тепла, передаваемого в выделенный объем от факелов горелки и дымовых газов; T – температура стабильного конденсата на выходе выделенного объема змеевика; TH – температура стабильного конденсата на входе выделенного объема змеевика; 
– объемная скорость поступления стабильного конденсата в выделенный объем змеевика; kT – удельная теплоемкость стабильного конденсата.
Если скорость изменения температуры сырья по длине змеевика является постоянной, то с учетом начальных условий
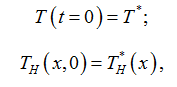
где T*– температура стабильного конденсата на выходе выделенного объема змеевика в момент времени t = 0; 
– температура стабильного конденсата на входе выделенного объема змеевика
в момент времени t = 0, уравнение (1) примет следующий вид:
(2)
Введя в рассмотрение безразмерные нормированные функции входного и выходного параметров
на основе (2), получим
Преобразуя
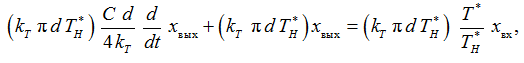(3)
получим
Приняв обозначения 
– постоянная времени объекта; 
– коэффициент пропорциональности объекта – и применив к (3) преобразование Лапласа, получим передаточную функцию Wo(s) объекта
Трубчатая печь является сложным многоемкостным объектом, поэтому для его описания целесообразно использовать передаточные функции более высоких порядков, отражающие наличие дополнительных внутренних тепловых емкостей. Практически используют второй или третий порядок полинома знаменателя передаточной функции, т. к. более высокие порядки вызывают затруднения в определении коэффициентов и не обеспечивают значительного повышения точности.
Передаточная функция трубчатой печи на установке У-121 по каналу «положение регулирующего клапана – температура стабильного конденсата на выходе печи», полученная методом Симою, определена как
Расчет многокаскадной системы предполагает наличие вспомогательных регулируемых параметров. Для рассматриваемой печи установки У-121
в качестве таких параметров выбраны расход топливного газа, поступающего на горелки, и температура дымовых газов на границе радиантной и конвективной камер.
Передаточная функция по каналу «положение регулирующего клапана – температура на границе радиантной и конвективной камер» 
определена как
Передаточная функция по каналу «положение регулирующего клапана – расход топливного газа, поступающего на горелки» 
определена как
Структура и расчет многокаскадной системы регулирования
Модель многокаскадной системы управления представлена на рис. 2.
Рис. 2. Модель многокаскадной системы управления трубчатой печью
Fig. 2. Model of a multi-cascade control system of a tubular furnace
Расчет многокаскадных систем отличается от каскадной наличием дополнительного ПИ-регулятора, методика расчета которого основана на методе Циглера – Никольса с учетом взаимовлияния регуляторов. Результаты расчета представлены в таблице, где C1 и C0 – настроечные параметры соответствующих регуляторов.
Результаты расчета многокаскадной системы управления
Results of calculation of multi-cascade control system
|
Номер регулятора |
C1, %х.р.о./°С |
C0, %х.р.о./°С×с |
|
1 итерация |
||
|
1 |
0,365 |
– |
|
2 |
0,0995 |
0,000645 |
|
3 |
2,52 |
0,002511 |
|
2 итерация |
||
|
1 |
0,363 |
– |
|
2 |
0,10017 |
0,000643 |
|
3 |
2,5335 |
0,002467 |
На второй итерации разница между настройками регуляторов составляет меньше 5 % (см. табл.). Расчет окончен.
Анализ полученных результатов
Рассмотрим переходные процессы по управляющему (рис. 3) и возмущающему воздействию (рис. 4) в одноконтурной, двухкаскадной и трехкаскадной системах.
Рис. 3. Переходный процесс в одноконтурной, двухкаскадной
и трехкаскадной системах по управляющему воздействию
Fig. 3. Transient process in single-loop, two-stage and three-stage systems according to control action
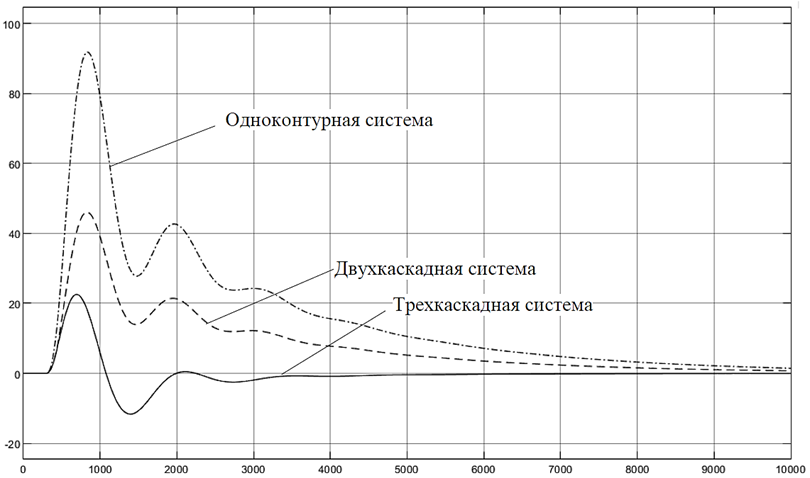
Рис. 4. Переходный процесс в одноконтурной, двухкаскадной
и трехкаскадной системах по возмущающему воздействию
Fig. 4. Transient process in single-circuit, two-cascade
and three-cascade systems according to the disturbing effect
Показатели качества переходного процесса одноконтурной системы по управляющему воздействию:
– время регулирования 6 700 с;
– перерегулирование отсутствует.
Показатели качества переходного процесса двухкаскадной системы по управляющему воздействию:
– время регулирования 6 640 с;
– перерегулирование отсутствует.
Показатели качества переходного процесса многокаскадной системы по управляющему воздействию:
– время регулирования 4 300 с;
– перерегулирование отсутствует.
Показатели качества переходного процесса одноконтурной системы по возмущающему воздействию:
– время регулирования 8 000 с;
– динамическое отклонение 91,9 °C.
Показатели качества переходного процесса двухкаскадной системы по возмущающему воздействию:
– время регулирования 8 000 с;
– динамическое отклонение 46,1 °C.
Показатели качества переходного процесса многокаскадной системы по возмущающему воздействию:
– время регулирования 3 300 с;
– динамическое отклонение 22,55 °C.
Показатели качества переходных процессов в трехкаскадной системе значительно превосходят одноконтурные и двухкаскадные системы управления по управляющему и возмущающему воздействиям (см. рис. 3, 4). Таким образом, для повышения эффективности управления трубчатой печи и аналогичных объектов со значительными транспортными и емкостными запаздываниями, обладающих большой инерционностью, целесообразно применять трехкаскадные системы автоматического управления. При этом реализация таких систем осуществляется на основе стандартных функциональных блоков ПИД-регулирования промышленных контроллеров.
Заключение
Предложена модель управления трубчатой печью на основе многокаскадной системы регулирования. Проведенные исследования показывают, что применение подобных систем регулирования позволяет увеличить экономичность и эффективность функционирования энергоемких производственных объектов.
1. Maslennikova S. V., Zhukova N. V. Analiz kaskadnykh skhem regulirovaniia trubchatykh pechei [Analysis of cascade control schemes for tubular furnaces]. Severgeoekotekh – 2015: materialy XVI Mezhdunarodnoi molodezhnoi nauchnoi konferentsii studentov, aspirantov i molodykh uchenykh (Ukhta, 25–27 marta 2015 g.): 6 chastiakh. Ukhta, Izd-vo UGTU, 2015. Part 1. Pp. 77-81.
2. Silin A. Iu., Gurovskii A. I., Gebel' E. S. Optimizatsiia sistemy upravleniia pech'iu trubchatoi blochnoi podogreva nefti PTB-5-40E [Optimization of the control system of the PTB-5-40E tubular block oil heating furnace]. Avtomatizatsiia, mekhatronika, informatsionnye tekhnologii: materialy XI Mezhdunarodnoi nauchno-tekhnicheskoi internet-konferentsii molodykh uchenykh (Omsk, 18–19 maia 2021 g.). Omsk, Izd-vo Omsk. gos. tekhn. un-ta, 2021. Pp. 108-114.
3. Kazakova V. N., Mikhailova P. G. Razrabotka i issledovanie sistem upravleniia s nechetkimi reguliatorami dlia ustanovki pervichnoi pererabotki nefti [Development and research of control systems with fuzzy regulators for the installation of primary oil refining]. Uspekhi v khimii i khimicheskoi tekhnologii, 2021, vol. 35, no. 3 (238), pp. 22-26.
4. Masiutina G. V., Lubentsov V. F. Sintez i analiz kaskadnoi sistemy upravleniia s nechetkim modifitsiro-vannym reguliatorom [Synthesis and analysis of a cascade control system with a fuzzy modified regulator]. Vestnik Severo-Kavkazskogo gosudarstvennogo tekhnicheskogo universiteta, 2010, no. 4, pp. 97-103.
5. Zaitsev S. V. Realizatsiia adaptivnykh reguliatorov v raspredelennykh sistemakh upravleniia [Implementation of adaptive controllers in distributed control systems]. Vestnik Astrakhanskogo gosudarstvennogo tekhnicheskogo universiteta. Seriia: Upravlenie, vychislitel'naia tekhnika i informatika, 2020, no. 3, pp. 99-104. DOI: https://doi.org/10.24143/2072-9502-2020-3-99-104.
