To improve the performance of machine learning algorithms in monitoring dynamic and unstable processes, it is necessary to carefully analyze the data structure forming the training sample. This stage is especially important in artificial intelligence systems, where the control object interacts with changing external conditions. Algorithms for analyzing the dynamics of randomness statistics and their application in monitoring dynamic systems are considered: the Hurst criterion is considered as a measure of the randomness of a series; The emergence score is an information indicator that is used to measure the degree to which the properties of a system cannot be fully explained or predicted based on the properties of its individual components; the fractal dimension score describes the complexity and self–similarity of an object's structure; the senior Lyapunov exponent is a key concept in the theory of dynamical systems that allows analyzing their sensitivity to initial conditions. The indicator helps to understand how the system reacts to the slightest changes in the source data. The Helder exponent evaluates a local measure of the regularity of a function. A new approach with averaging within each window is proposed, which increases the efficiency of the analysis and reduces the risk of false periodic components. An example of the application of the described methods for estimating the uncertainties that arise when determining the state of complex technical systems is given (based on fragments of time series from an open database). Numerical results of a study of time series nonlinearity and randomness statistics using a sliding window are presented. The presented combined estimation algorithm allows us to consider the evaluation system as a generalized representation of a segment of a series of observations, which creates the basis for solving one of the key tasks of machine learning – the creation of generalized models of the dynamics of state vectors. These models are used in clustering and use case analysis tasks. To process multidimensional time series, it is proposed to use a specialized method based on their singular value decomposition.
technical systems diagnostics, chaotic time series, randomness statistics, fractal dimension, Hoelder index, Hurst criterion, Lyapunov exponent, emergence
Введение
Идентификация нестационарных негауссовых временных рядов позволяет обнаружить аномалии в структурах данных и является актуальной задачей в различных областях [1–3], в числе которых диагностика состояния сложных технических систем и прогнозирование его изменения. При анализе данных, порождаемых нестационарными процессами, обычно последовательно проверяются гипотезы нелинейности, хаотичности и применимости моделей динамического или стохастического хаоса [4, 5].
Если в ходе анализа данных выявляется хотя бы один положительный показатель Ляпунова λ, то процесс определяется как хаотический. Ключевой метрикой таких процессов является средний горизонт предсказуемости, обратно пропорциональный показателю Ляпунова, обозначаемый как 1 / λ. Помимо показателей Ляпунова, в комплексном анализе хаотических систем рассматриваются фрактальные размерности, показатель Гёльдера, критерий Хёрста, статистики Хинича, эмерджентность и другие показатели [6–9].
Одной из ключевых характеристик хаотических систем является их способность к чередованию состояний равновесия и активности. В общем случае такие системы могут функционировать в двух различных режимах:
1. Длительное пребывание в состоянии относительной стабильности, когда уровень активности системы минимален или колеблется в незначительных пределах вблизи точки равновесия. Эти участки фазовой траектории часто называют окнами или руслами.
2. Внезапные и непредсказуемые переходы от состояния покоя к периодам высокой активности, которые также могут быстро затухать. Эти участки именуются джокерами. Для описания таких явлений используются термины бифуркации и катастрофы.
Механизмы формирования специфических участков в упорядоченных фазах (ламинарных окнах или руслах) и кратковременных, непредсказуемых всплесков активности (джокеров), а также их объединение и классификация представляют собой задачу сегментации [6–9]. В любой системе периодически происходят всплески активности, которые возникают самопроизвольно и не поддаются значительному внешнему влиянию. Временные интервалы между всплесками, их продолжительность, амплитуда и другие характеристики не следуют каким-либо строгим закономерностям, но могут быть описаны с использованием вероятностных моделей. Согласно теории самоорганизованной критичности [10], представляющей собой междисциплинарный методологический подход, который предназначен для исследования сложных динамических систем, стремящихся к состоянию на грани хаоса, случайные флуктуации инициируют формирование высокоорганизованных нелинейных паттернов и структур, проявляющихся в виде каскадов событий – лавин. На ранних этапах перехода системы к критическому состоянию наблюдается значительное усиление частоты хаотических всплесков, а также увеличение продолжительности локальных квазипериодических режимов. Эти процессы характеризуются высокой чувствительностью к начальным условиям, что обусловливает их крайнюю восприимчивость
к внешним воздействиям и внутренним флуктуациям.
В технических науках теория самоорганизованной критичности применяется для анализа сложных сигналов и систем. Ключевым аспектом является изменение характеристик огибающей сигнала, что проявляется в вариациях амплитуды и частоты колебаний. Эти изменения приводят к возникновению новых свойств и закономерностей в поведении системы, открывая перспективы для разработки инновационных методов обработки сигналов и оптимизации технических процессов.
Постановка задачи
Прерывистое равновесие – это явление, которое наблюдается во многих областях. Оно может приводить к необъяснимым сбоям в работе объектов и оборудования критической инфраструктуры в различных областях. Одним из признаков приближения сбоя являются вторичные эффекты, вызванные изменениями в хаотичности наблюдаемого процесса.
Степень упорядоченности хаоса можно оценить с помощью геометрии фракталов. Однако для этого необходимо усреднять показатели хаотичности по достаточно длинным отрезкам ряда, что может противоречить ограничениям на горизонт прогноза.
Таким образом, при мониторинге нестационарных систем возникают задачи, требующие оперативного контроля динамики статистик хаотичности, предполагающие:
– уменьшение ширины окна при одновременном снижении дисперсии оценок;
– выявление статистики хаотичности, изменяющейся монотонно в случае накопления неустойчивости;
– применение системы оценки параметров для создания общей характеристики части ряда;
– выявление участков, на которых наблюдается «шум мерцания», что может указывать на внезапное изменение процесса.
Обобщенные портреты динамических систем могут использоваться в процедурах кластеризации, прецедентного анализа и краткосрочного прогнозирования.
Алгоритмы анализа динамики статистик хаотичности
Рассмотрим алгоритмы анализа динамики статистик хаотичности [11–14].
Статистика критерия Хёрста. Применение метода Хёрста к временному ряду позволяет проанализировать долговременные тенденции временного ряда и определить, присутствуют ли в нем тренды, циклические колебания или случайные отклонения.
Алгоритм получения статистики критерия Хёрста:
1) отрезок ряда Y длиной L центрируется и для него находится оценка среднеквадратичного отклонения s;
2) строится его кумулятивная сумма Z;
3) для ряда Z вычисляется его размах
;
4) находится статистика (показатель) Хёрста:
. (1)
Показатель Хёрста представляет собой статистический инструмент для оценки степени стохастичности временных рядов. Его значения, близкие
к 0,5, указывают на хаотическую природу исследуемого процесса. Участкам, на которых 
отрезок ряда сохраняет общую тенденцию монотонности. Значения 
соответствуют участкам, на которых восходящая тенденция сменяется нисходящей или наоборот. При приближении ht к 1 устойчивость становится заметнее.
Оценка эмерджентности. Эмерджентность – информационный показатель, позволяющий понять, какие взаимодействия и взаимосвязи между элементами системы приводят к появлению новых качеств и возможностей и как эти качества могут быть использованы для достижения целей системы.
Алгоритм оценивания показателя эмерджентности системы:
1) отрезок ряда Y длиной L аппроксимируется кубическим сплайном Z;
2) вычисляются интерполированные значения на решетке с достаточно малым шагом Δ;
3) по интерполированным значениям строится гистограмма H с числом узлов, приходящихся на длину L;
4) гистограмма H нормируется и в ней удаляются нулевые элементы;
5) показатель эмерджентности рассчитывается по формуле
(2)
Энтропия отражает степень беспорядка или неопределенности в системе, которая изменяется со временем. Она показывает, насколько быстро система теряет информацию о своем текущем состоянии. Отношение ht / I близко к величине 1,21, поэтому эти статистики в значительной степени уточняют и дополняют друг друга.
Оценка фрактальной размерности. Классический «поточечный» метод базируется на вычислении расстояний от произвольной точки до всех элементов анализируемого набора данных.
Алгоритм определения фрактальной размерности [15]:
1) рассматривается набор данных 
, который представляет собой выборку из m-мерного пространства за определенный период времени;
2) вокруг каждого элемента выборки строится сфера радиуса r;
3) подсчитывается количество случаев M(x, r), которые попадают внутрь сферы;
4) определяется вероятность того, что случайно выбранный элемент окажется внутри сферы, определяется как отношение M(x, r) к общему числу элементов в выборке
5) проводится оценка фрактальной размерности.
При малых значениях r вероятность P(x, r) определяется как 
, где Dt обозначает хаусдорфову размерность множества и вычисляется по формуле
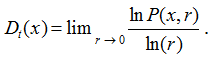(3)
Для некоторых множеств размерность остается неизменной независимо от выбора элемента. Однако для многих других множеств размерность Dt может варьироваться в зависимости от выбора элемента x. В таких случаях целесообразно использовать усредненную поточечную размерность.
При обработке данных часто встречаются пропуски, нарушающие непрерывность функции P(x, r) по параметру r. Для вычисления усредненной поточечной размерности выбирается случайное подмножество данных размером L / N, и для каждого случая определяются значения P(x, r). Усредненная хаусдорфова размерность множества вычисляется по специальной формуле:
Значение L определяется опытным путем. Для этого мы начинаем с небольшого числа и постепенно увеличиваем его до тех пор, пока не достигнем предела. В данном случае выражение (3) будет выглядеть как
(4)
где – граничные значения радиуса. Для статистик ht и Dt должно выполняться соотношение
.
Статистики (1)–(4) для одних и тех же данных вычисляются по различным формулам независимо, но выражаются друг через друга, поэтому на их основе можно строить уточненную комбинированную оценку, например фрактальной размерности Dt. Этот алгоритм принят в расчетах, приводимых ниже.
Старший показатель Ляпунова λ. Если имеется ансамбль траекторий 
динамической системы с близкими начальными значениями 
, то можно определить показатель λ скорости разбегания любых двух траекторий в окрестности точки t0 из соотношения
откуда получаем
(5)
Для комплексного анализа системы необходимо определить среднее значение по всем возможным траекториям и параметрам t и t0. Этот метод применяется для вычисления старшего показателя Ляпунова.
В спектре параметра λ можно увидеть группы значений, которые соответствуют средним показателям подчиненных индикаторов. Эти данные образуют спектр Ляпунова. Сумма всех положительных значений спектра Ляпунова коррелирует с энтропией системы.
Алгоритм нахождения старшего показателя Ляпунова по временному ряду x(t):
1) временной ряд разделяется на заданное количество интервалов (полос) m;
2) для каждого интервала фиксируются все точки, попавшие в него;
3) точки с номером k рассматриваются в каждом интервале как начальные точки для ансамбля близких траекторий;
4) находятся ближайшие по времени в соседних интервалах точки с номерами k + D и k – D, где D – заданная величина отклонения;
5) для каждой пары точек в интервале вычисляется частная оценка по формуле (5);
6) полученные частные оценки усредняютcя по всем точкам, всем интервалам и нескольким значениям параметра D.
Показатель Гёльдера. В анализе данных и разработки моделей машинного обучения показатель Гёльдера применяется для оценки гладкости функций, описывающих взаимосвязи между признаками. Это позволяет создавать более точные и производительные модели. Показатель Гёльдера α в точке t0 определяется как
или
где t берется в окрестности точки t0. Для всего отрезка ряда берется наименьшая из полученных частных оценок.
Показатель Гёльдера характеризует локальную регулярность функции. Если значение показателя больше или равно единице, функция считается гладкой, а если меньше единицы – сингулярной в данной точке. Состояние нормы характеризуется показателем Гёльдера, не превышающим единицу. Существенное отклонение данного показателя в большую или меньшую сторону может указывать на нарушения в функционировании системы. Рост показателя Гёльдера может служить сигналом о приближении кризисных режимов.
Пример
Рассмотрим возможность применения описанных методов для оценивания неопределенностей, возникающих при определении состояния сложных технических систем [16–20]. В качестве примера взят фрагмент временного ряда из базы данных [21] (рис. 1, а).
Рис. 1. Динамика изменения показателей сигнала от датчика [21]: а – сигнал; б – значения первых разностей сигнала
Fig. 1. Сhanges of dynamics in signal parameters from the sensor [21]: а – the signal; б – the first signal differences values
Для идентификации нестационарности и негауссовости временных рядов применяются стандартные методики, включающие вычисление первых и вторых разностей. На рис. 1, б проиллюстрированы значения первых разностей сигналов, приведенных на рис. 1, а, показывающие резкие скачки скорости – зоны, где могут проявиться неожиданные изменения.
Оценка старшего показателя Ляпунoва в исследуемом временном ряду по методикам, приведенным в работах [7–9], демонстрирует его стабильность в диапазоне от 0,18 до 0,22 на протяжении всего анализируемого периода. Это факт подтверждает присутствие хаотической динамики и позволяет сделать вывод о возможности прогнозирования на среднем горизонте.
В работе [10] предлагается формировать оценки для последовательной системы окон, а усреднение осуществляется в 2 этапа: на 1-м этапе применяется двустороннее экспоненциальное сглаживание с небольшим коэффициентом дисконтирования; на 2-м этапе процесс оценки повторяется с различными параметрами окна, а полученные частные оценки усредняются.
В настоящей работе предлагается подход с усред-
нением внутри каждого окна, который значительно повышает оперативность анализа (примерно в 2–3 раза) и снижает риск появления ложных периодических составляющих.
Результаты численных исследований
При анализе различных версий статистики
в скользящем окне применяются следующие обозначения:
– L – размер скользящего окна;
– d – шаг сдвига окна;
– m – число зон, на которые разбивается область значений отрезка ряда;
– α – коэффициент дисконтирования при двустороннем экспоненциальном сглаживании;
– D – число полос при изучении отклонений;
– L0 – длина предшествующего участка относительной устойчивости – «русла».
На представленных ниже графиках используются следующие параметры: L = 100, d = 1, α = 0,05,
m = 20, D = 4, L0 = 300. Таким образом, был проведен анализ 243 временных рядов из базы [21], аналогичных представленным на рис. 1. В результате были выявлены 4 основных варианта поведения пар статистических показателей «показатель Гёльдера» – «фрактальная размерность» за 100 с до резкого скачка, или «джокера». Для наглядности каждый раз приводится поведение тех же показателей за предыдущие 300 с.
В 40 % случаев перед скачком наблюдается рост обоих показателей – на рис. 2 наблюдается участок русла (измерения 1 : 300) и начало участка джокера (измерения 301 : 400), при этом следует отметить рост обоих показателей.
Рис. 2. Совместная динамика фрактальной размерности и показателя Гёльдера:
а – динамика фрактальной размерности; б – динамика показателя Гёльдера; в – показатель Гёльдера
Fig. 2. The joint dynamics of the fractal dimension and the Helder index:
a – the dynamics of the fractal dimension; б – the dynamics of the Helder index; в – the Helder index
В 40 % случаев перед скачком растет показатель Гёльдера, что свидетельствует о повышении гладкости траектории при сохранении фрактальной размерности (рис. 3).
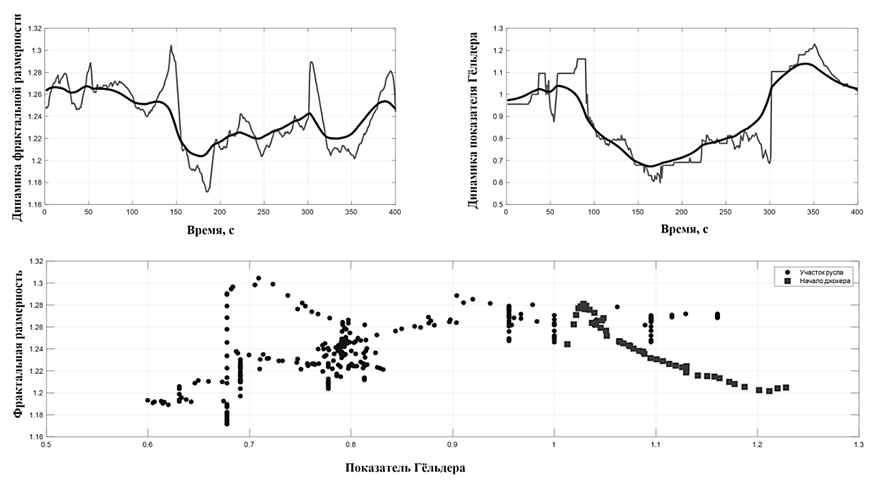
Рис. 3. Повышение показателя гладкости при постоянстве фрактальной размерности:
а – динамика фрактальной размерности; б – динамика показателя Гёльдера; в – показатель Гёльдера
Fig. 3. Increasing the smoothness index with a constant fractal dimension:
a – the dynamics of the fractal dimension; б – the dynamics of the Helder index; в – the Helder index
В 10 % случаев перед скачком возрастает фрактальная размерность при неизменной или даже снижающейся характеристике гладкости траектории (рис. 4).
Рис. 4. Рост фрактальной размерности; низкие значения показателя гладкости указывают на сингулярность
данного отрезка ряда: а – динамика фрактальной размерности; б – динамика показателя Гёльдера;
в – показатель Гёльдера
Fig. 4. An increase in the fractal dimension; low values of the smoothness index indicate the singularity of this segment
of the series: a – dynamics of the fractal dimension; б – dynamics of the Helder index; в – the Helder index
В 10 % случаев перед скачком фрактальная размерность уменьшается при неизменной или даже снижающейся гладкости траектории (рис. 5).
Рис. 5. Снижение фрактальной размерности; низкие значения показателя гладкости указывают на сингулярность
данного отрезка ряда: а – динамика фрактальной размерности; б – динамика показателя Гёльдера;
в – показатель Гёльдера
Fig. 5. A decrease in the fractal dimension; low values of the smoothness index indicate the singularity
of this segment of the series: a – dynamics of the fractal dimension; б – dynamics of the Helder index; в – the Helder index
Процент проявления различных вариантов поведения рассматриваемых статистик хаотичности основан на фрагменте базы данных [21] – всего 243 примера.
Случай, представленный на рис. 5, демонстрирует аномалию. Более глубокий анализ показывает, что такие ситуации возникают при наложении двух очень близких, но разнонаправленных скачков. Такое сочетание называют коррекцией. Остальные типовые ситуации демонстрируют лишь множественность вариантов проявления нелинейности, которые невозможно связать с направлением скачка [13, 15].
Регулярная динамика традиционно рассматривается как предшественник хаотического поведения. Однако, как показано в [1], типичные временные ряды, генерируемые сложными системами в нормальных условиях, не являются строго регулярными. Иными словами, в таких системах показатель Гёльдера должен быть не более единицы. Отклонение этого значения от нормы в большую или меньшую сторону указывает на дисфункцию системы. Данный метод используется для исследования временных рядов, характеризующих сложные системы, с целью выявления аномальных отклонений. Предполагается, что динамика временного ряда будет следовать аналогичной тенденции. Увеличение показателя Гёльдера может служить индикатором приближения кризисного состояния, тогда как его снижение может указывать на предстоящий качественный скачок.
Комбинированный алгоритм оценивания
Рассматриваемая методика базируется на использовании комбинации методов оценки на скользящем окне, корректировки оценки фрактальной размерности и вычисления показателя Гёльдера. Для выявления характера нелинейности применяется ряд методов: корреляционный размерный тест, тест BDS, биспектральный тест Хинича, тест НЕГМА, тест Уайта, тест Каплана [7, 9, 13].
Поскольку нелинейность может проявляться в различных формах, не существует универсального теста, который превосходил бы другие в обнаружении и анализе этого явления. Все упомянутые тестовые статистики могут быть изучены в рамках подхода, предложенного в данной работе, однако признаки приближения к скачку формулируются довольно расплывчато и, вероятно, не могут быть использованы в автоматизированном режиме.
Для создания вероятностного распределения прогнозов была использована комбинация из 24 статистических тестов. Однако результат оказался многовершинным, что затрудняет выделение основных сценариев. Удается выделить лишь несколько наиболее вероятных вариантов [13].
Критические отклонения значений рассмотренных статистик составили всего несколько процентов от локального среднего. Для их выявления использовался алгоритм накопленных сумм. На рис. 6 представлено изображение характерного участка, предшествующего скачку, а также накопленные суммы, центрированные относительно предыдущего контрольного участка длиной L.
а б
Рис. 6. Кумулятивные суммы и пороги обнаружения для участка,
приведенного на рис. 2: а – фрактальная размерность участка перед скачком;
б – показатель Гёльдера для участка перед скачком
Fig. 6. Cumulative amounts and detection thresholds for the area shown in Fig. 2:
a – the area before the jump fractal dimension; б – the area before the jump Golder indicator
Порог обнаружения установлен на основе правила «трех сигм» по тому же контрольному участку до сглаживания.
В результате применения комбинированного алгоритма оценивания, основанного на множестве статистических тестов, удалось выявить признаки приближения к скачку. Вероятностные распределения прогнозов, полученные на основе 24 тестов, показали многовершинность, что затрудняет однозначную интерпретацию, но позволяет выделить несколько наиболее вероятных сценариев.
Заключение
В работе представлена новая методика построения статистики-индикатора ожидаемого скачка. Она базируется на комбинации оценки на скользящем окне, корректировке оценки фрактальной размерности и вычислении показателя Гёльдера. Для контрастирования динамики этих статистик применяется метод кумулятивных сумм.
Хаотические сигналы характеризуются сложной структурой, которая, в свою очередь, делает их информативными. Это позволяет использовать их в задачах анализа динамических систем и проводить раннюю диагностику:
– в случае проведения исследования в реальном масштабе времени динамика статистик хаотичности может применяться для оценки тенденций;
– в случае проведения анализа и прогнозирования на основе прецедентов оценки статистик хаотичности показатели выступают в роли «портретов» отрезков ряда наблюдений.
В задачах диагностики сложных технических систем изменение параметров нелинейности и хаотичности можно ассоциировать с развитием деградационных процессов. Для анализа многомерных рядов измерений предлагается применять метод сингулярных проекций.
1. Kuznetsov A. P., Sedova Yu. V., Stankevich N. V. Coupled systems with quasi-periodic and chaotic dynamics. Chaos, Solitons & Fractals, 2023, vol. 169, p. 113278. DOI:https://doi.org/10.1016/j.chaos.2023.113278.
2. Sel'chenkova N. I., Uchaev A. Ia. Issledovanie kriticheskogo povedeniia dinamicheskikh sistem [Investigation of the critical behavior of dynamical systems]. Iadernaia fizika i inzhiniring, 2024, vol. 15, no. 1, pp. 48-56. DOI:https://doi.org/10.56304/S2079562923010220.
3. Timoshchuk A. S. Navigatsiia v dinamicheskom khaose [Navigating through dynamic chaos]. Aktual'nye problemy gumanitarnykh i sotsial'no-ekonomicheskikh nauk, 2024, no. 2 (102), pp. 114-120.
4. Kuznetsov S. P. Dinamicheskii khaos [Dynamic chaos]. Izvestiia vysshikh uchebnykh zavedenii. Prikladnaia nelineinaia dinamika, 2002, vol. 10, no. 1-2, pp. 189-191.
5. Roy S., Majumdar S. Chaos, stochasticity and noise. Noise and randomness in living system. Singapore, Springer Singapore, 2022. Pp. 145-154. DOI:https://doi.org/10.1007/978-981-16-9583-4_14.
6. Anishchenko V. S. Znakomstvo s nelineinoi dinamikoi [Introduction to nonlinear dynamics]. Moscow, URSS Publ., 2007. 221 p.
7. Bezruchko B. P., Smirnov D. A. Matematicheskoe modelirovanie i khaoticheskie vremennye riady [Mathematical modeling and chaotic time series]. Izvestiia vysshikh uchebnykh zavedenii. Prikladnaia nelineinaia dinamika, 2006, vol. 14, no. 1, pp. 153-157.
8. Shashikhin V. N. Interval'nye dinamicheskie sistemy: modeli, analiz, sintez [Interval dynamical systems: models, analysis, synthesis]. Saint Petersburg, Izd-vo SPbGPU, 2003. 213 p.
9. Shashikhin V. N. Khaos i nelineinaia dinamika. Reguliarnaia i khaoticheskaia dinamika: uchebnoe posobie [Chaos and nonlinear dynamics. Regular and chaotic dynamics: a study guide]. Saint Petersburg, Izd-vo Politekhn. un-ta, 2010. 210 p.
10. Bak P., Paczuski M. Complexity, contingency, and criticality. Proceedings of the National Academy of Sciences, 1995, vol. 92, no. 15, pp. 6689-6696.
11. Doinikov A. N., Sal'nikova M. K. Metodika prognozirovaniia nestatsionarnykh protsessov v mnogosviaznykh sistemakh s peremennoi strukturoi [Methodology for forecasting nonstationary processes in multiconnected systems with variable structure]. Sistemy. Metody. Tekhnologii, 2009, no. 1, pp. 53-58.
12. Cencini M., Falcioni M., Olbrich E., Kantz H., Vul-piani A. Chaos or noise: Difficulties of a distinction. Physical Review E., 2000, vol. 62, no. 1, p. 427. DOI:https://doi.org/10.1103/PhysRevE.62.427.
13. Corduas M. Mining time series data: A selective survey. Data Analysis and Classification: Proceedings of the 6th Conference of the Classification and Data Analysis Group of the SocietàItaliana di Statistica. Springer Berlin Heidelberg, 2010. Pp. 355-362. DOI:https://doi.org/10.1007/978-3-642-03739-9_40.
14. Roberts M., SenGupta I. Sequential hypothesis test-ing in machine learning, and crude oil price jump size detection. Applied Mathematical Finance, 2020, vol. 27, no. 5, pp. 374-395. DOI:https://doi.org/10.1080/1350486X.2020.1859943.
15. Muller N. V. Modelirovanie i identifikatsiia vremennykh riadov v komp'iuternykh sistemakh s ispol'zovaniem fraktal'nogo i veivlet-analiz. Avtoreferat dissertatsii … kand. tekhn. nauk [Modeling and identification of time series in computer systems using fractal and wavelet analysis. Abstract of the dissertation ... Candidate of Technical Sciences]. Komsomol'sk-na-Amure, 2017. 19 p. Available at: https:// so-vet.knastu.ru/media/files/_EPtkDA.PDF (accessed: 21.12.2024).
16. Makshanov A. V., Tyndykar' L. N. Prognozirovanie i segmentatsiia nestatsionarnykh dannykh dlia rannego obnaruzheniia strukturnykh skachkov [Forecasting and segmentation of non-stationary data for early detection of structural jumps]. Sovremennye vyzovy transportnoi otrasli: novye vozmozhnosti: materialy Mezhvuzovskoi nauchno-prakticheskoi konferentsii transportnykh vuzov (Moskva, 27–28 fevralia 2024 g.). Moscow, Dashkov i K Publ., 2024. Pp. 153-157.
17. Makshanov A. V., Zhuravlev A. E., Tyndykar L. N. A new approach to identifying the local structure of multidimensional chaotic time series. Journal of Physics: Conference Series, 2021, vol. 2142, no. 1, p. 012011. DOI:https://doi.org/10.1088/1742-6596/2142/1/012011.
18. Makshanov A., Musaev A., Grigoriev D. Analyzing and forecasting financial series with singular spectral analysis. Dependence Modeling, 2022, vol. 10, no. 1, pp. 215-224. DOI:https://doi.org/10.1515/demo-2022-0112.
19. Musaev A., Makshanov A., Grigoriev D. Statistical analysis of current financial instrument quotes in the conditions of market chaos. Mathematics, 2022, vol. 2, no. 4, p. 587. DOI:https://doi.org/10.3390/math10040587.
20. Rafael' M. Y., Musaev A. A., Grigoriev D. A. Evaluation of statistical forecast method efficiency in the conditions of dynamic chaos. 2021 IV International Conference on Control in Technical Systems (CTS). IEEE, 2021. Pp. 178-180.
21. Download Free Forex Data. HistData.com. Available at: https://www.histdata.com/download-free-forex-data/?/excel/1-minute-bar-quotes (accessed: 24.12.2024).
