FSUE Atomflot (Chief Mate)
Russian Federation
Russian Federation
Russian Federation
Russian Federation
Towing is one of the most difficult and risky tasks of navigation, since in this case two or more vessels are involved simultaneously. A minimal number of towing-related accidents have been recorded, but they still occur, and the issue remains of improving the safety of such operations. Many years of research and practical experience in conducting towing operations confirm the direct dependence of the safety of their conduct on the trajectory of the towed vessel. The results of the analysis indicate that the disadvantage of existing methods of towing vessels is the yawing of the towed vessel, which leads to an unnecessarily large loss of speed even in light seas, which is mainly caused by the presence of external disturbances. It is proved that in order to increase the safety of towing operations, it is necessary to stabilize the yaw of the towed vessel. An algorithm has been developed to stabilize the ship's course, which allows it to solve the problem of towing along a given trajectory. The algorithm is based on the model of angular motion of the vessel, which operates with the angular velocity of the towed vessel and the angle of rudder adjustment. Such a model of the angular motion of a towed vessel is used, in which this speed can be controlled by the effects of the angle of the rudder. At the same time, the stabilization algorithm “converges” to a stable course even in the presence of significant external disturbances. The resulting mathematical model is solved using the least squares method and is capable of both stabilizing and minimizing the yaw of the towed vessel. The proposed empirical method for assessing the stability of the course of a towed vessel can provide additional navigational safety for towing operations.
stabilization algorithm, safety of towing operations, towing of the vessel, yawing of the towed vessel, the trajectory of movement
Введение
Обзор аварийности судов на море свидетельствует о низком уровне аварийности при потере и/или повреждении буксируемого объекта, однако аварии, допущенные в результате потери управляемости в ходе буксировки, все еще случаются и, следовательно, необходима проработка вопросов повышения безопасности при проведении буксирных операций по заданной траектории.
Теоретические исследования [1–5] подтверждают, что все буксируемые суда обладают рыскливостью, которую с точки зрения безопасности нужно нивелировать до допустимых пределов, т. е. стабилизировать их движение. Особенно остро эта проблема возникает при наличии серьезных внешних возмущений, обусловленных действием ветра и волны.
Рыскание буксируемого судна приводит к достаточно большой потере в скорости, поэтому целесообразно разработать алгоритм, позволяющий стабилизировать движение буксируемого судна, особенно при развитом волнении на море, и иметь производную от величины рыскания, в которой была бы минимально возможная составляющая от возмущения, вызывающая это рыскание. При составлении алгоритма стабилизации движения буксируемого судна и минимизации процесса его рыскания будем использовать такую модель углового движения буксируемого судна, в которой этой скоростью можно управлять воздействиями от угла перекладки руля.
Постановка задачи
Восстановление модели рыскания буксируемого судна можно осуществить с помощью полной модели углового движения судна, но такая модель сложна в реализации. Поэтому, основываясь на известном упрощении дифференциального уравнения углового движения буксируемого судна, используем для реализации стабилизации и уменьшения по модулю величины рыскания судна на буксире упрощенную модель вида:
![]() (1)
(1)
причем далее будем рассматривать модель движения устойчивого судна.
Уравнение (1) имеет два настраиваемых параметра: постоянную времени 1 / Т и коэффициент эффективности руля kδ. Ввиду сложной зависимости параметров Т и kδ от конкретных эксплуатационных условий буксировки желательно автоматически подстраивать эти параметры на основании информации об угловой скорости буксируемого судна ω и угла перекладки руля δ(t). Таким образом, задача состоит в том, чтобы при заданной структуре математической модели углового движения буксируемого судна и на основании измерений ω(t) и δ(t) осуществлять идентификацию параметров модели Т и kδ, которые способны как стабилизировать, так и минимизировать рыскание буксируемого судна.
Если параметры 1 / Т и kδ / T точно не известны, что равноценно изменению режима эксплуатации буксируемого судна, то при подстановке значений данных от реального буксируемого объекта dω(t) / dt, dω(t) и δ(t) в выражение (1) равенство не будет соблюдаться. Поэтому обозначим невязку уравнения (1) через ε(t), а параметры модели a1 = 1 / T и a2 = = kδ / T, тогда
![]() .
.
Качество идентификации параметров a1 и a2 можно оценивать с помощью метода наименьших квадратов с весовой функцией вида:
![]() .
.
Весовую функцию f(t) можно выбрать, например, из условия так, чтобы квадрат невязки е2(t) учитывался с тем большим весом, чем позже она была получена. Функцией f(t), удовлетворяющей этому условию, является экспонента
![]() .
.
Коэффициент затухания экспоненты α характеризует интервал осреднения квадрата невязки е2(t) и может быть подобран экспериментально. В дальнейшем будем предполагать, что процесс рыскания буксируемого судна наблюдается достаточно долго, чтобы принять нижний предел в критерии равным –∞. Таким образом, чтобы стабилизировать и минимизировать рыскание буксируемого судна, критерий задается так:
 .
.
Стабилизация процесса рыскания буксируемого судна
Необходимым условием минимума критерия будет выполнение системы уравнений относительно параметров а1 и а2:

Запишем эти условия:
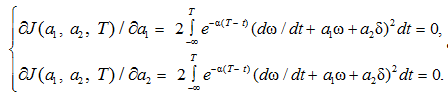
Примем, что объект стационарен на интервале осреднения, задаваемом экспоненциальной весовой функцией, поэтому коэффициенты ai и а2 можно выносить за знак интеграла:
 (2)
(2)
Полученную систему линейных уравнений можно разрешить относительно a1 и а2 или в векторной форме:
 .
.
Перепишем систему уравнений (2):
![]() . (3)
. (3)
Для получения решений вектора а* в рекуррентной форме продифференцируем равенство (3) по Т:
 .
.
Обозначив обратную матрицу
![]()
и взяв производную от γ(T), получим систему уравнений для рекуррентного расчета параметров:
 (4)
(4)
Если взять в качестве матрицы γ(Т) принужденное решение, при котором правая часть уравнения (4) обращается в нуль, то можно несколько упростить полученный алгоритм [1]. В данном случае таким принужденным решением будет выражение вида:
![]() .
.
Подставим это принужденное решение в уравнение для производной dа*/ dT и получим:
![]() .
.
В скалярной форме оно может быть записано так:
 (5)
(5)
Использование для упрощения полученного алгоритма принужденного решения уравнений (4) способно повлиять на его сходимость, поэтому далее целесообразно исследовать сходимость алгоритма (4). Пусть а10 и а20 – истинные значения искомых параметров, другими словами – соблюдается равенство (1):
![]() .
.
Тогда можно записать невязку уравнений в виде:
![]() .
.
Перепишем уравнения поиска (5) с учетом составленной невязки ε(t) и стационарности движения буксируемого судна (а10 = const и а20 = const):
 (6)
(6)
Алгоритм (6) сходится в смысле монотонного уменьшения суммы квадратов ошибок величины
![]() .
.
Действительно, производная от этой величины с учетом выражения (6):
![]() .
.
Так как производная является отрицательной величиной, это означает, что рыскание не может увеличиваться, следовательно, можно признать – алгоритм будет сходиться и обеспечивать стационарность движения буксируемого судна.
Обсуждение полученных результатов
Долгое время научные исследования в части повышения безопасности проведения буксирных операций проводились в направлении повышения эффективности управления буксирующим судном [4]. Однако безопасность выполнения буксирных операций в целом во многом зависит от траектории движения буксируемого судна, особенно если имеются дополнительные внешние возмущения. Это требует проведения дополнительных эмпирических исследований, определения способов и методов управления системой «буксир – буксируемое судно» для решения задачи обеспечения устойчивости движения буксируемого судна, т. е. минимизации его рыскания [6–8].
В работе представлен алгоритм, позволяющий стабилизировать движение буксируемого судна при отягчающих внешних факторах. В основу алгоритма положена модель углового движения судна, включающая угловую скорость буксируемого судна и угол перекладки руля. Доказано схождение предложенного алгоритма, который обеспечивает стационарность движения буксируемого судна.
Заключение
Доказанная возможность стабилизации рыскания буксируемого судна и составленный алгоритм такой стабилизации позволяют решить задачу буксировки по заданной траектории.
Алгоритм стабилизации «сходится» даже при наличии внешних существенных возмущений и позволяет обезопасить проведение буксирных операций по системе «буксир – буксируемое судно».
1. Brazhnyi A. I. Navigatsionnaia bezopasnost' karavana pri morskikh i okeanskikh buksirovkakh plavuchikh sooruzhenii: dis. … kand. tekhn. nauk [Navigation safety of a caravan during sea and ocean towing of floating structures: dis. ... Candidate of Technical Sciences]. Murmansk, 2018. 168 p.
2. Gurov P. V. Upravliaemost' buksirnogo sostava v slozhnykh putevykh i meteorologicheskikh usloviiakh: avtoreferat dis. ... kand. tekhn. nauk [Controllability of the tow train in difficult track and meteorological conditions: ab-stract of the dissertation of the Candidate of Technical Sciences]. Nizhnii Novgorod, 2013. 20 p.
3. Iudin Iu. I., Ishcheikin G. Iu. Modelirovanie izmenenii dliny i natiazheniia trosa v protsesse vypolneniia buksirnoi operatsii [Modeling of cable length and tension changes during the towing operation]. Morskie intel-lektual'nye tekhnologii, 2020, no. 4-4 (50), pp. 8-12.
4. Iudin Iu. I., Ishcheikin G. Iu. Upravlenie dvizheniem buksiruemogo sudna putem izmeneniia natiazheniia i dliny buksirnogo trosa [Controlling the movement of the towed vessel by changing the tension and length of the tow rope]. Ekspluatatsiia morskogo transporta, 2022, no. 4 (105), pp. 10-19.
5. Kaian V. V. Razrabotka bezopasnykh sposobov manevrirovaniia sudna pri vypolnenii buksirnykh operatsii: av-toreferat dis. ... kand. tekhn. nauk [Development of safe ways of maneuvering a vessel when performing towing op-erations: abstract of the dissertation of the Candidate of Technical Sciences]. Murmansk, 2014. 22 p.
6. Iudin Iu. I., Kaian V. V. Sposob upravleniia traektoriei dvizheniia buksiruemogo sudna [A method for controlling the trajectory of a towed vessel]. Patent RF, no. 2011115725/11, 27.12.2012.
7. Iudin Iu. I., Vlasov A. V., Kaichenov A. V., Viskov A. Iu. Sposob upravleniia dvizheniem buksirnoi sistemy [The method of motion control of the towing system]. Patent RF, no. 2015143563/15, 11.04.2017.
8. Iudin Iu. I., Pashentsev S. V. Otsenka bezopasnosti buksirnoi operatsii metodami matematicheskogo modeli-rovaniia [Assessment of the safety of the towing operation by mathematical modeling methods]. Moscow, Morkniga Publ., 2015. 142 p.

















